Способы определения случайных событий
Для определения вероятностей случайных событий используют непосредственные и косвенные схемы подсчетов. При непосредственном подсчете различают априорную и апостериорную схемы подсчетов: А). Априорная схема подсчетов – априорно (до опыта) подсчитывают число опытов m, в которых событие появилось, и общее число произведенных опытов n. Б). Апостериорная схема подсчетов – апостериорно (после опыта) подсчитают число опытов m, в которых событие появилось, и общее число произведенных опытов n. Косвенные схемы подсчетов – схемы, основанные на аксиоматической теории. Здесь события определяются как множества, над которыми можно осуществлять все теоретико-множественные операции. Теория множеств является логическим фундаментом современной теории вероятности и была предложена в 1933 г. А.Н. Колмогоровым. Им сформулированы основные аксиомы теории вероятностей. Аксиома 1. Поле событий F(A) является алгеброй множеств. Эта аксиома указывает на аналогию теории множеств и теории вероятности. Аксиома 2. Каждому множеству Ar из F(A) поставлено в соответствие действительное число P (Ar), называемое вероятностью события Ar .
Аксиома 3. Вероятность достоверного события равна 1:
Аксиома 4. Если А1 и A2 несовместны, то вероятность суммы этих событий равна сумме их вероятностей
при условии
1.1.2. Определение априорной вероятности Вероятность элементарного события определяется как
где n – количество элементарных событий (возможных исходов). Вероятность случайного события
где pir – вероятности элементарных событий При априорной численной оценке появления элементарных случайных событий, как правило, принимаются равновероятные исходы Тогда вероятность случайного события определится формулой
где
|


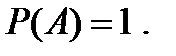

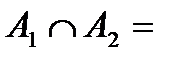 Ø или для множества несовместных событий
Ø или для множества несовместных событий Ø;,
Ø;, 
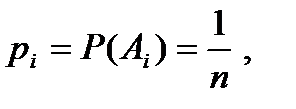


 , входящих в подмножество
, входящих в подмножество 


 – количество благоприятных исходов.
– количество благоприятных исходов.


