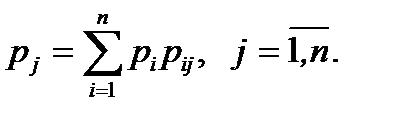Марковские цепи
На практике часто встречаются системы, состояния которых образуют цепь, в которой каждое состояние si (кроме крайних s 0 и sn) связано прямой и обратной связями с двумя соседними
Примером такой системы является техническое устройство, состоящее из однотипных узлов. Каждое состояние системы характеризуется числом неисправных в данный момент времени t узлов. При анализе случайных процессов с дискретными состояниями важную роль играют вероятности состояний – вероятности событий, состоящих в том, что в момент времени t система S будет в состоянии si:
Очевидно, что в любой момент времени t сумма вероятностей состояний: Определение 7.1. Случайный процесс, протекающий в системе S с дискретными состояниями, называют марковским, если для любого момента времени t 0 вероятность каждого из состояния системы в будущем (при t>t 0) зависит только от её состояния в настоящем (t=t 0) и не зависит от того, когда и как она пришла в это состояние, то есть не зависит от её поведения в прошлом (t<t 0). При дискретном времени изменения состояний системы каждый переход от одного состояния к другому состоянию называют шагом. Из определения марковской цепи следует, что для нее вероятность перехода системы S в состояние на k +1 шаге зависит только от того, в каком состоянии sj находилась система на предыдущем k -ом шаге. Основной задачей исследования является нахождение вероятностей состояния si на любом k -ом шаге
Для нахождения этих вероятностей необходимо знать условные вероятности перехода системы S на k -ом шаге в состояние sj, если известно, что на предыдущем k –1-ом шаге она была в состоянии si. Обозначим эти вероятности как
Вероятности pij(k) называют переходными вероятностями марковской цепи на k -ом шаге. Вероятность pij есть вероятность того, что на k -ом шаге системы останется в состоянии si. Цепь Маркова называют однородной, если переходные вероятности не зависят от номера шага: pij(k)=pij =const. Переходные вероятности записываются в виде квадратной матрицы размера
Вероятность состояния системы на следующем шаге определяется по рекуррентной формуле:
Цепь Маркова называется неприводимой, если в ней содержится не более одного замкнутого множества. Цепь Маркова неприводима, в частности, тогда, когда все ее состояния достижимы друг от друга. Состояние i называется периодическим, если существует такое t>;1, что вероятность перехода из i в i за n шагов равна нулю при всех n, не кратных t. Цепь, не содержащая периодических состояний, называется непериодической. Определение 7.2. Непериодическая неприводимая цепь Маркова называется эргодической. При этих условиях (эргодичность, однородность, отсутствие циклов) в цепи Маркова устанавливается стационарный режим, в котором вероятности состоянии системы уже от номера шага не зависят
Такие вероятности называют предельными (или финальными) вероятностями цепи Маркова
Вероятность переходов непосредственно записывается на стрелках графа марковской цепи. Пример размеченного графа состояний системы S показан на Рисунке 7.3. Рисунок 7.3. – Размеченный граф
|

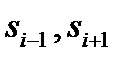 , а крайнее – с одним соседним (Рисунок 7.2).
, а крайнее – с одним соседним (Рисунок 7.2).
 и определяется как сумма вероятностей полной группы несовместных событий.
и определяется как сумма вероятностей полной группы несовместных событий.