Энтропия. Неопределенность события определяется вероятностью его появления, неопределенность СВ – числовой характеристикой функции плотности вероятностей
Неопределенность события определяется вероятностью его появления, неопределенность СВ – числовой характеристикой функции плотности вероятностей, например, вторым центральным моментом (или дисперсией). Однако для случайных процессов (объектов) или явлений, состояния которых различаются качественно, а не количественно, использование дисперсии невозможно. В общем случае мера неопределенности, связанная с распределением вероятности, должна быть некоторой ее числовой характеристикой, не зависящей от того, в какой шкале измеряются реализации случайного процесса или явления. В качестве такой меры К. Шеннон предложил использовать энтропию Н для случайного процесса Х:
где р 1, р 2,…, рn – вероятности случайных событий а 1, а 2,…, аn, характеризующие возможные состояния случайного процесса α;. При этом
Из формул (8.1) (8.2) следует, что неопределенность отсутствует только в том случае, когда одно из значений рi равно 1. Максимальная неопределенность достигается при р 1= р 2...= рn = Принцип максимума информации (энтропии) был сформулирован Джейнсом (Jenes Principal). Этот принцип имеет фундаментальное значение для различных приложений к системам и процессам в физике, химии и биологии. Его доказательство в нашем случае сводится к следующему. Потребуем, чтобы условие
выполнялось при ограничении
Экстремум (8.1) при ограничении (8.2) может быть найден с помощью метода множителей Лагранжа. Суть метода состоит в том, что (8.2) умножается на неизвестный пока постоянный параметр λ, и затем полученное произведение прибавляется к левой части уравнения (8.1)
Затем определяется экстремум
Из последнего выражения следует, что рi =const. Тогда из условия npi =1, Из равенства
Для равнозначного распределения вероятностей неопределенность возрастает с увеличением n. Последнее свидетельствует о том, что энтропия (8.1) является как мерой неопределенности, так и мерой разнообразия. Это означает, что чем сложнее случайный процесс, тем большей неопределенностью он обладает, или другими словами, тем менее прогнозируемыми становятся объекты или явления. В случае, когда α; представляет собой континуум (
Основание логарифма в формулах (8.1), (8.2) не оказывает качественного влияния на оценку энтропии, а лишь определяет её размерность. Для непрерывных случайных процессов при теоретическом анализе, включающем интегрирование и дифференцирование математических выражений, наиболее удобно использовать натуральные логарифмы. При этом энтропия определяется в натуральных единицах – нитах (или хартли). В более общем случае информационная энтропия (макроэнтропия) для непрерывных случайных процессов имеет размерность времени (секунда). В термодинамике на молекулярном уровне вводится понятие энергетической энтропии (микроэнтропии), которая определяется количеством тепла. Размерность микроэнтропии – джоуль (Дж). При анализе цифровых машин и других устройств, работающих в двоичном коде, как правило, используются двоичные логарифмы и соответственно двоичные единицы – биты. При анализе измерительных устройств, работающих в десятичном коде, удобнее применять десятичные логарифмы и десятичные единицы – диты. Между этими единицами существуют определенные соотношения: 1 дит=2,3 нит=3,3 бит; 1нит=1,45 бит=0,43 дит; 1 бит=0,69 нит=0,3 дит. Пример 8.1. Для такого объекта как монета (подбрасывание монеты) характерны два равновероятных случайных состояния (события): выпадение решки или орла. Энтропия этого явления
Пример 8.2. Для бутерброда также возможны два состояния: хлеб и масло. На основании известного в народе «закона» о том, что бутерброд всегда падает маслом вниз,
При n =2 неопределенность исхода в подбрасывании максимальна в случае с монетой; для бутерброда неопределенность отсутствует.
|



 , то есть когда существует равновероятное распределение случайных событий, отражающих состояние случайного процесса (объекта или явления).
, то есть когда существует равновероятное распределение случайных событий, отражающих состояние случайного процесса (объекта или явления).




 определяется вероятность
определяется вероятность 

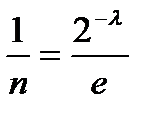 вычисляется множитель Лагранжа:
вычисляется множитель Лагранжа:
 ) (например, для случайной величины Х, принимающей бесконечное несчетное множество значений (
) (например, для случайной величины Х, принимающей бесконечное несчетное множество значений ( )), энтропия вычисляется по формуле
)), энтропия вычисляется по формуле






