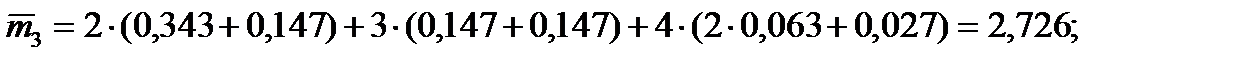Формирование экономичного кода алфавита
Для наиболее распространенного двоичного кода среднее число двоичных элементарных сигналов Если Неравномерный побуквенный код Код называется однозначно декодируемым, если любая последовательность символов из A единственным способом разбивается на отдельные кодовые слова. Пример 10.1. Для источника 1) 2) 3) 4) первые три кода однозначно декодируемы, последний код – нет. Если ни одно кодовое слово не является началом другого, код называется префиксным. Префиксные коды являются однозначно декодируемыми. В примере 10.1 префиксным кодом является код
10.2.1. Код Шеннона–Фано Для построения неравномерного экономичного кода Р. Фано и К. Шенноном предложена следующая методика (код Шеннона–Фано): 1. Все 2. Разбивают все буквы на две группы (верхнюю I и нижнюю II) так, чтобы вероятности для букв к каждой из этих групп были по возможности близки одна к другой. 3. Для букв первой группы в качестве первой цифры кодового обозначения используется цифра 1, а для букв второй группы – цифра 0. 4. Каждую из двух полученных групп снова делят на две части наиболее близкой суммарной вероятности; 5. Присваивают буквам вторую цифру кодового обозначения: 1 или 0 в зависимости от того, принадлежит буква к первой или ко второй из этих более мелких групп. 6. Каждую из содержащих более одной буквы групп снова делят на две части наиболее близкой суммарной вероятности и т.д. 7. Процесс повторяется до тех пор, пока каждая из групп не будет содержать одну единственную букву. Алгоритм построения кода Шеннона–Фано приводится в Приложении 4. Пример 10.2. Возьмем алфавит, состоящий из 6 букв, вероятности которых равны 0,4; 0,2; 0,2; 0,1; 0,05; 0,05. Необходимо составить код Шеннона–Фано. Решение. Наилучший равномерный код состоит из трехзначных кодовых обозначений, так как в соответствии с (10.1): 22<6<23.Поэтому в нем на каждую букву приходится три элементарных сигнала. Результаты решения по составлению кода Шеннона–Фано удобно представить в виде таблицы 10.1 и кодового дерева (Рисунок 10.1). При использовании кода Шеннона–Фано среднее число элементарных сигналов, приходящихся на одну букву,
Это значительно меньше трех и очень близко к предельно минимальному значению
Таким образом, получен экономичный код. Еще более экономичным получается код, если по методу Шеннона–Фано кодировать не отдельные буквы, а блоки букв, n –буквенные блоки. Пример 10.3. Возьмем алфавит, состоящий из двух букв А и В, имеющих вероятности р (А)=0,7; р (В)=0,3. Энтропия:
Таблица 10.1. – Порядок составления кода Шеннона–Фано
Рисунок 10.1. – Кодовое дерево
Двухбуквенный алфавит можно привести к простейшему равномерному коду: 1 – для А и 0 – для В, требующему для передачи каждой буквы один двоичный знак. Это на 0,12 (12 %) больше минимально достижимого значения Н. Требуется определить среднее значение длины кода в двух- и трехбуквенных сообщениях. Решение. Представим коды двух- и трехбуквенных комбинаций, построенные по методу Шеннона–Фано (таблица 10.2). Трехбуквенный код формируется 4 префиксными кодовыми деревьями, формируемыми из l =2, 3, 4 кодовых слов (последняя колонка таблицы 10.2).
Таблица 10.2. – Результаты вычислений
б). Трехбуквенный код: n =3 Рисунок 10.2. – Кодовые деревья двух- и трехбуквенного кодов
Среднее значение длины кода для n =2:
или на одну букву
что на 3,4 % отличается от минимально достижимого значения Н. Среднее значение длины кода для n =3:
или на одну букву
что на 3,8 % отличается от минимально достижимого значения Н. Представленные примеры отражают суть основной теоремы Шеннона о кодировании при отсутствии помех: При кодировании сообщения, разбитого на n –буквенные блоки, можно, выбрав n достаточно большими, добиться того, чтобы среднее число двоичных элементарных сигналов, приходящихся на одну букву исходного сообщения, было сколь угодно близко к энтропия Н. Иначе: Очень длинное сообщение из m букв может быть закодировано при помощи сколь угодно близкого к m·Н числа элементарных сигналов, если только предварительно разбить это сообщение на достаточно длинные блоки из n букв и сопоставить отдельные кодовые обозначения (кодовые слова) сразу целым блокам.
|

 , приходящихся в закодированном сообщении на одну букву исходного сообщения, не может быть меньше
, приходящихся в закодированном сообщении на одну букву исходного сообщения, не может быть меньше  , то есть
, то есть  , где
, где 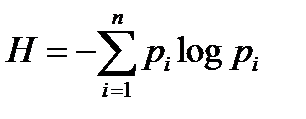 – энтропия одной буквы. Исходя из этого, при любом методе кодирования для записи длинного сообщения из
– энтропия одной буквы. Исходя из этого, при любом методе кодирования для записи длинного сообщения из 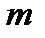 букв требуется не меньше чем
букв требуется не меньше чем 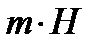 двоичных знаков. Это обстоятельство вытекает из условия, что
двоичных знаков. Это обстоятельство вытекает из условия, что  , и что все буквы независимы между собой. В этом случае
, и что все буквы независимы между собой. В этом случае 
 , то
, то  Отсюда следует, что учет статистических закономерностей сообщения позволяет построить более экономичный, чем равномерный код. Такой код является неравномерным.
Отсюда следует, что учет статистических закономерностей сообщения позволяет построить более экономичный, чем равномерный код. Такой код является неравномерным. объемом
объемом  над алфавитом A определяется как произвольное множество последовательностей одинаковой или различной длины из букв алфавита A.
над алфавитом A определяется как произвольное множество последовательностей одинаковой или различной длины из букв алфавита A. среди четырех кодов:
среди четырех кодов:

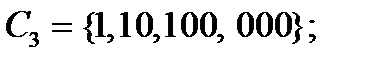

 Префиксные коды удобно представлять в виде кодовых деревьев (Рисунок 10.1).
Префиксные коды удобно представлять в виде кодовых деревьев (Рисунок 10.1). букв (или иных знаковых систем) располагается в столбик в порядке убывания вероятностей, их появления в сообщении.
букв (или иных знаковых систем) располагается в столбик в порядке убывания вероятностей, их появления в сообщении.



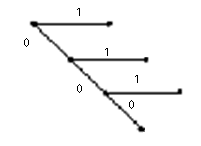 а). Двухбуквенный код: n =2
а). Двухбуквенный код: n =2 l =2
l =2 l =3
l =3 l =4
l =4 l =4
l =4