Код Хаффмена

Самым экономичным (оптимальным) из всех возможных является код Хаффмена: ни для какого другого метода кодирования букв некоторого алфавита среднее число элементарных сигналов, приходящихся на одну букву, не может быть меньше того, какое получается при кодировании по методу Хаффмена. Построение этого кода опирается на простое преобразование, называемое сжатием алфавита. Суть этого метода такова.

1. Буквы а ₁, а ₂, …, а_{n -1}, a_n алфавита А располагают в порядке убывания вероятностей их появления: p ₁≥ p ₂ ≥…≥ p_{n -1} ≥ p_n.

2. Две последние буквы принимают за одну - b, получая новый алфавит А ₁, состоящий из букв а ₁, а ₂,…, b с вероятностями р ₁, р ₂,…, (р_{n -1}+ р_n). Эта операция называется однократным сжатием. Буквы алфавита А ₁ располагаются в порядке убывания вероятностей.

3. Аналогичным образом подвергается сжатию алфавит А ₁. Эта операция по отношению к алфавиту А называется двукратным сжатием. В результате этой операции получается алфавит А ₂, содержащий n –2 буквы, который также располагают в порядке убывания вероятностей.

4. Операция сжатия продолжается до тех пор, пока не образуется алфавит А_{n -2}, содержащий всего две буквы ((n –2) - кратное сжатие). Этим буквам присваивают кодовые обозначения 1 и 0.

5. Если кодовое обозначение уже приписано всем буквам алфавита A_j, то буквам предыдущего алфавита A_{j -1}, сохранившимся и в алфавите A_j, приписываются те же кодовые обозначения, которые они имели в алфавите A_{j -1}, двум буквам и алфавита A_j, слившимся в букву b алфавита A_{j -1}, приписываются обозначения, получающиеся из кодового обозначения буквы b добавлением 1 и 0 в конце.

Пример 10.4. Исходный алфавит А состоит из 6 букв с вероятностями использования 0,4; 0,2; 0,2; 0,1; 0,05; 0,05 соответственно. Требуется осуществить кодирование алфавита по методу Хаффмена.

Решение. В нашем случае n =6. Используя четырехкратное сжатие исходного алфавита, получаем алфавит A ₄, содержащий 1 и 0. Результаты вычислений представлены в таблице 10.3. Кодирование алфавита по методу Хаффмена позволяет всегда построить кодовое дерево, аналогичное тому, которое было получено в частном случае при кодировании кодом Шеннона–Фано (Рисунок 10.1 примера 10.2). Код является префиксным, допускает однозначное декодирование.

Среднее число элементарных сигналов, приходящихся на одну букву:

Таким образом, экономичность кодов для примеров 10.2 и 10.4 одна и та же.

Для кодов с основанием k основная теорема о кодировании при отсутствии помех может быть представлена следующим образом.

При любом методе кодирования, использующем код с основанием k,

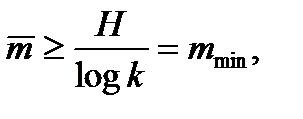
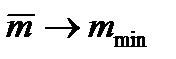где Н – энтропия одной буквы сообщения. При этом , если кодировать сразу блоки, состоящие из n букв.

Таблица 10.3. – Результаты вычислений