Условная энтропия
Если α; и β; – независимые случайные объекты (явления), то
то есть энтропия двух или нескольких независимых объектов или явлений равна сумме энтропий этих объектов или явлений. Это свойство аддитивности энтропии. Если α; и β; – зависимые случайные объекты или явления, то
где Н(β\α) или Н(α; Для всех случайных объектов или явлений имеет место неравенство Н (α;)≥ Н (α; Пример 8.3. Неопределенность даты проведения ежегодного мероприятия можно определить двумя путями:
где 365 – число дней в году;
где 12 – число месяцев в году; 30 – число дней в месяце. Пример 8.4. Специалист, занимающийся проблемой В, для информационного обеспечения своей интеллектуальной деятельности воспользовался автоматизированной информационно – поисковой системой (АИПС). В базе АИПС содержится 2% статей, непосредственно относящихся к заданной проблеме. Система поиска в АИПС точно обнаруживает эти статьи по запросу. В то же время ввиду некоторой близости тематики других статей к проблеме В эта система с равной вероятностью может представить или не представить специалисту статьи, не относящиеся непосредственно к проблеме В. Определить эффективность системы поиска, используя меру снятия неопределенности по отношению к проблеме В. Решение. Формализуем представленную ситуацию. Определение отношения той или иной статьи к проблеме В представим как опыт β;, имеющий два возможных исхода: В 1 – не относится; В 2 – относится. Определение эффективности системы поиска представим как опыт А 1 – определен признак В; А 2 – не определен признак В. Вероятности определения и неопределения признака В соответственно равны:
Неопределенность отношения той или иной статьи к проблеме В:
Это есть неопределенность базы АИПС по отношению к проблеме В. В целом, с учетом эффективности работы системы поиска, то есть опыта α;, неопределенность АИПС можно вычислить через условную энтропию Н(α\β). Для этого определим: 1) условные вероятности исходов В 1 и В 2 опыта β; при условии исходов А 1 и А 2 опыта α;:
так как из 51 случая, когда система поиска давала положительный ответ, 49 статей не относились к проблеме В, а 2 статьи относились,
что вполне очевидно; 2) Условные энтропии АИПС (при условии исходов А 1 и А 2):
Тогда средняя условная энтропия опыта β; (неопределенность АИПС) при условии существования системы поиска (опыт α;) будет равна математическому ожиданию энтропии условного распределения
Если сравнить значение
|



 определяются как математические ожидания энтропии условного распределения (условной энтропии).
определяются как математические ожидания энтропии условного распределения (условной энтропии). может только уменьшить неопределенность
может только уменьшить неопределенность  , а если они независимы (
, а если они независимы (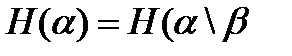 ), то оставить её неизменной.
), то оставить её неизменной.

 , также имеющий две возможных исхода:
, также имеющий две возможных исхода:



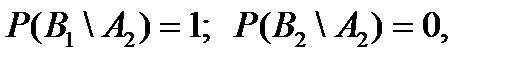
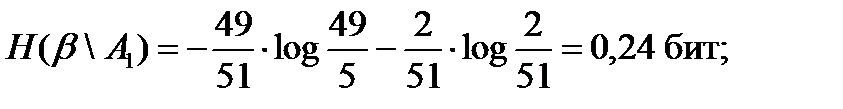

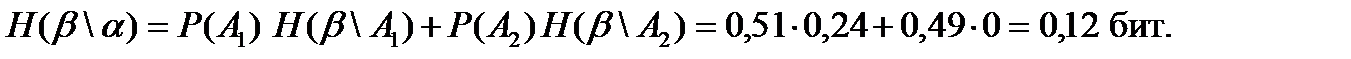
 с ранее полученным значением неопределенности базы АИПС
с ранее полученным значением неопределенности базы АИПС  , то можно сделать вывод, что система поиска недостаточно эффективна, поскольку снимает неопределенность всего на 2 %.
, то можно сделать вывод, что система поиска недостаточно эффективна, поскольку снимает неопределенность всего на 2 %.


