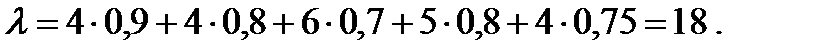Потоки событий

В частном случае поток событий можно представить как последовательность точек v₁,v₂,..,v _n на оси времени t с разделяющими их интервалами T₁,T₂,…,T _n (Рисунок 6.2): T₁=v₂-v₁, T₂=v₃-v₂, …,T _{n -1}=v _n -v _{n -1}.

Рисунок 6.2. – График потока событий

Потоки событий обладают следующими свойствами: ординарностью, без последствия, стационарностью.

Ординарным называют поток, если события в нем возникают поодиночке, а «не пачками». Это означает, что вероятность попадания на участок ∆t двух и более событий пренебрежительно мала по сравнению с вероятностью попадания на него ровно одного события:

Потоком без последствия называют поток, в котором для любых непересекающихся участков времени (Рисунок 6.3) число событий, попадающих на эти участки, X ₁= x (t ₁, ), X ₂= x (t ₂, ),…, X_n = x (t_n, ) представляет собой независимую СВ.

Рисунок 6.3. –Поток без последствия

Стационарным называют поток, если его вероятностные характеристики не меняются со временем. В частности, для стационарного потока событий вероятность попадания того или иного числа событий на участок длиной зависит только от длины этого участка и не зависит от того, где на оси времени t этот участок расположен.

Поток событий, обладающий всеми тремя перечисленными свойствами, называют простейшим пуассоновским потоком. Для простейшего потока событий вероятность того, что на участке длиной наступит ровно k событий, определяется по формуле (предельная теорема)

(6.1)

где λ;=const – интенсивность потока, равная математическому ожиданию числа событий, наступающих в единицу времени.

Согласно предельной теореме сумма ординарных стационарных потоков событий сходится к простейшему пуассоновскому потоку.

При сложении n независимых стационарных потоков будет получен простейший поток, интенсивность которого равна сумме интенсивностей складываемых потоков

(6.2)

Предельная теорема для суммарного потока дает теоретическое обоснование для использования в ряде практических задач, в предположении, что фигурирующие в них потоки является пуассоновским.

Пример 6.2. В многопользовательской информационной системе одновременно работают 5 человек с производительностью каждого λ₁=4; λ₂=4; λ₃=6; λ₄=5; λ₅=4 (запросов в час).Вероятность ввода некорректного запроса, на который будет получен отказ системы, – q ₁=0,1; q ₂=0,2; q ₃=0,3; q ₄=0,2; q ₅=0,25. Найти вероятность того, что количество ответов системы составит не менее 14 в час.

Решение. Интенсивность корректных запросов определяется формулой (6.2)

где p_i =1– q_i, =1 (час),

Тогда

Вероятность искомого события

Здесь