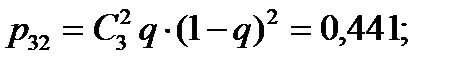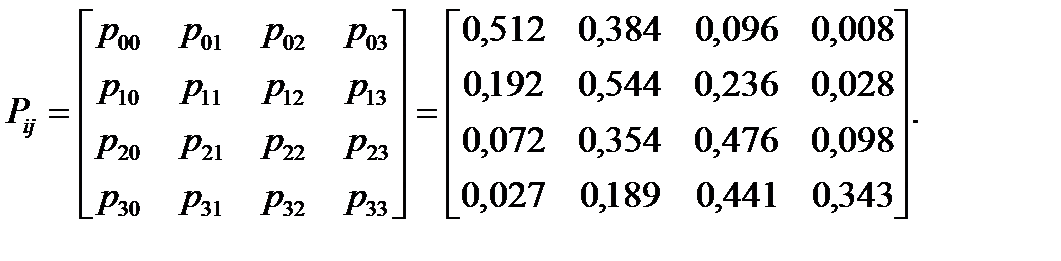Расчет цепи Маркова для стационарного режима

Для нахождения финальных вероятностей необходимо составить систему алгебраических уравнений, исходя из правила – для стационарного режима суммарный поток, переводящий систему из других состояний в состояние s_j, равен суммарному потоку вероятностей событий, выводящих систему из состояния s_j

(7.7)

К этим уравнениям надо добавить нормировочное условие , отбросив одно любое из уравнений (7.7). Полученная система уравнений с n неизвестными имеет единственное решение.

 

Пример 7.1. Вычислительная машина находится в одном из следующих состояний: s ₁ – исправно работает; s₂ – несправна, тестируется; s₃ – неисправна, настраивается программное обеспечение; s ₄ – находится на профилактике; s ₅ – ремонтируется, модернизируется. Размеченный граф состояний показан на Рисунке 7.4. Составить систему уравнений и найти предельные вероятности состояний.

Решение. Рассмотрим состояние s ₅. В это состояние направленно две стрелки. Поэтому согласно (7.7) в левой части уравнения для j= 5 будут два слагаемых. Следовательно, в правой части будет одно слагаемое. Таким образом,

Аналогично запишем уравнения для вершин 2, 3, 4:

 

Рисунок 7.4. – Размеченный граф состояний к примеру 7.1

 

В качестве пятого уравнения возьмем условие нормировки

Уравнение для узла s ₁ отбрасываем. Его можно затем использовать для контроля полученного решения.

Перепишем систему уравнений в виде

;

В результате решения системы линейных алгебраических уравнений (СЛАУ) методом подстановок получим

p ₁=0,597; p ₂=0,1; p ₃=0,071; p ₄=0,066; p ₅=0,166.

 

Пример 7.2. В локальной вычислительной сети работают три ЭВМ. Через определенные промежутки времени t все ЭВМ тестируются, в результате чего каждая признается либо исправной, либо требующей ремонта. Вероятность того, что за время t исправная ЭВМ выйдет из строя, равна r, а что неисправная будет отремонтирована, равна q. Процессы выхода ЭВМ из строя и их восстановление протекают независимо друг от друга. Полагая, что r =0,2; q =0,3, найти финальные вероятности.

Решение. Построим граф состояний (Рисунок 7.5), нумеруя их по числу исправных ЭВМ: s ₀ – нет ни одной неисправной, s ₁ – одна неисправна, s ₂ – две неисправны, s ₃ – все три неисправны.

Рисунок 7.5. – Граф состояний

 

Для того чтобы система перешла из состояния s ₀ в s ₁, нужно, чтобы одна из трех ЭВМ за время t вышла из строя.

Эта вероятность определяется согласно закону распределения Бернулли

Аналогично находим:

Для проверки убедимся, что

Для того чтобы система из состояний s ₁ перешла в состояние s ₀, нужно, чтобы неисправная ЭВМ за время t была отремонтирована (А), а две исправные не вышли из строя (В). Тогда

Аналогично находим

Проверочное условие:

Рассуждая подобным образом, определим оставшиеся вероятности:

Проверочное условие:

Проверочное условие:

Из вычисленных вероятностей составим переходную матрицу при r =0,2; q =0,3

Для определения финальных вероятностей выпишем СЛАУ (7.6):

с исключенным третьим узлом s ₃:

После преобразований получим СЛАУ AX=B:

Протокол решения СЛАУ (программа в М-файле MatLab) имеет вид:

Таким образом, искомые финальные вероятности равны: