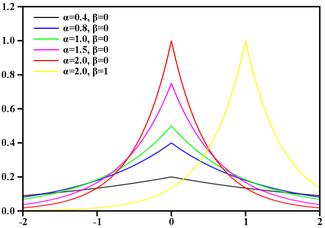
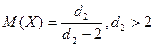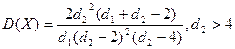Распределение Лапласа.
Случайная величина
Функция распределения имеет вид:
Параметры: 1.Математическое ожидание
2.Дисперсия
3.Характеристическое уравнение
4.Начальный момент r-ого порядка
8.Медиана
9.Мода
19. Распределение хи-квадрат ( Плотность вероятности этой случайной величины вычисляется по формуле:
Здесь
Функция распределения имеет вид:
Параметры: 1.Математическое ожидание
2.Дисперсия
Характеристическая функция
4.Начальный момент r-ого порядка:
7.Центральный момент r-ого порядка:
8.Медиана
9.Мода
20. Распределение хи ( Плотность вероятности равна:
Функция распределения имеет вид:
Параметры: 1. Математическое ожидание M(x) = 2. Дисперсия
3.Характеристическое уравнение
4.Начальный момент r-ого порядка
8.Мода
F-распределение (распределение Снедекора). Плотность вероятности этой случайной величины вычисляется по формуле:
, где
Параметры: 1.Математическое ожидание
2.Дисперсия
8.Медиана нет 9.Мода
|
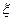имеет распределение Лапласа (двустороннее экспоненциальное распределение) с параметром 
и 
, если ее функция плотности вероятностей имеет вид: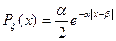
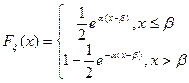
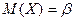
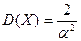
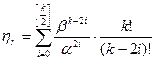
2- распределение)
- гамма-функция Эйлера. 
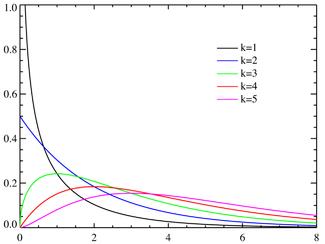
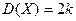
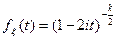
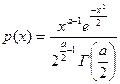, x>0
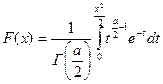
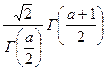
- гамма-функция.
