Распределение Бернулли.
Говорят, что случайная величина
Функция распределения случайной величины
Параметры:
1.Математическое ожидание M(x) = 0∙(1-p)+1∙p=p 2.Дисперсия
3.Характеристическая функция f 4.Начальный момент r-го порядка
5.Абсолютный момент r-го порядка 6.Факториальный момент r-го порядка f 7.Центральный момент r-го порядка
8.Медиана нет 9.Мода
Биноминальное распределение. Для биномиального распределения вероятность принятия случайной величиной Y значения y определяется формулой
где число сочетаний из n элементов по y, известное из комбинаторики. Для всех y, кроме 0, 1, 2, …, n, имеем P(Y=y)= 0. Функция распределения имеет вид:
Параметры:
1.Математическое ожидание M(y) = np 2.Дисперсия
3.Характеристическая функция f 4.Начальный момент r-го порядка
5.Абсолютный момент r-го порядка
6.Факториальный момент r-го порядка 7.Центральный момент r-го порядка
8.Медиана Одно из 9.Мода
|

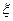 имеет распределение Бернулли с параметром p, если
имеет распределение Бернулли с параметром p, если 



 =(0-p)
=(0-p)  ∙(1-p)+(1-p)
∙(1-p)+(1-p)  (t)=
(t)=  +
+  = 1-p+
= 1-p+  =q+
=q+  =
= 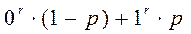 =p
=p =p
=p =p
=p =
= 
 = (0-
= (0-  ∙(1-p)+ (1-
∙(1-p)+ (1-  max(p,q)
max(p,q)


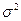 = np (1-p)= npq
= np (1-p)= npq
 =
= 
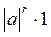 =
= 

 ∙1=0
∙1=0
 (n+1)p
(n+1)p


