Полиномиальное распределение (мультиномиальное распределение).Совместное распределение вероятностей случайных величин
принимающих целые неотрицательные значения
удовлетворяющие условиям
с вероятностями
где
Ранг матрицы B равен k − 1 в силу того, что Характеристическая функция:
При
стремится к некоторому многомерному нормальному распределению, а распределение суммы
которая используется в математической статистике при построении χ2-критерия, стремится к χ2-распределению с k − 1 степенями свобод
|
, 
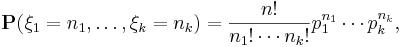
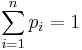; является многомерным дискретным распределением случайного вектора 
такого, что: 
(по существу это распределение является (k − 1)-мерным, так как в пространстве 
оно вырождено); естественным (с точки зрения современной теории вероятностей)
и ковариационную матрицу 
, где
.
распределение случайного вектора 
с нормированными компонентами
=a)=1
, 
, 
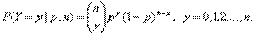
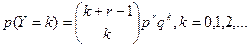
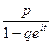
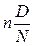
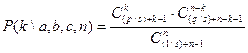
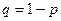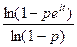
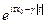
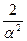
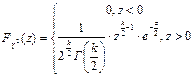
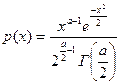
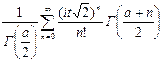
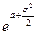
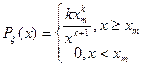
25.Фишера
26.Вейбула-Гнеденко
