Распределение Симпсона.Cлучайная величина ξ имеет треугольное распределение (распределение Симпсона) на отрезке [ a, b ] (a < b), если
Параметры:
1.Математическое ожидание
2.Дисперсия
3.Характеристическая функция
4.Начальный момент r-ого порядка:
Показательное (экспоненциальное) распределение. Непрерывная случайная величина
Функция распределения F
Параметры: 1.Математическое ожидание 2.Дисперсия
3.Характеристическая функция.
8.Медиана
9.Мода
Нормальное распределение Случайная величина
Функция распределения F (x) имеет соответственно вид:
Параметры: 1.Математическое ожидание
Введем рассмотренную замену x=a+st. Получим
Таким образом параметр a равен математическому ожиданию нормального распределения. 2.Дисперсия
С помощью той же замены получим
Применим интегрирование по частям
Таким образом, параметр s равен среднеквадратическому отклонению нормального распределения. 3.Характеристическое уравнение
|
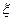имеет показательное распределение с параметром 
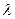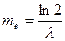
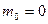
> 0, если она принимает только неотрицательные значения, а 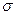ее плотность распределения p 
= 
= 
= 
│ 
= 
, 
>0, если ее плотность распределения p 
