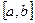Распределение Пуассона.
Случайная величина
Функция распределения имеет вид:
Параметры:
1.Математическое ожидание M(x)= 2.Дисперсия
3.Характеристическая функция f 8.Медиана нет 9.Мода
Логарифмическое распределение. Функция вероятности имеет вид:
Функция распределения имеет вид:
Параметры:
1.Математическое ожидание M(x)= 2.Дисперсия
3.Характеристическая функция f f 8.Медиана нет 9.Мода
Распределение Бореля-Таннера. Дискретное распределение вероятностей случайной величины ξ, принимающей значения
где r > 0 — целое и 0 < α < 1. Параметры:
1.Математическое ожидание 2.Дисперсия
11. Непрерывная случайная величина
Функция распределения
Параметры: 1.Математическое ожидание 2.Дисперсия
Замена переменной где c = (b – a)/2. 3.Характеристическая функция
7.Центральный момент r-го порядка
8.Медиана
9.Мода Любое число из отрезка
|

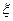 имеет распределение Пуассона, если
имеет распределение Пуассона, если 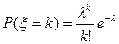 ,где λ>0 – параметр распределения Пуассона.
,где λ>0 – параметр распределения Пуассона.


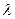
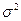 =
= 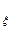 (t)=
(t)= 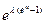
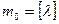
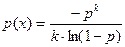
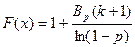 , где
, где  - неполная бета-функция
- неполная бета-функция

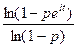
 =M(x
=M(x 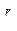 )=
)= 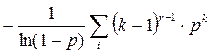


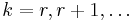 с вероятностями
с вероятностями

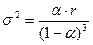
 Равномерное распределение.
Равномерное распределение. , принимающая значения на отрезке [ a, b ], распределена равномерно на [ a, b ], если ее плотность распределения p
, принимающая значения на отрезке [ a, b ], распределена равномерно на [ a, b ], если ее плотность распределения p 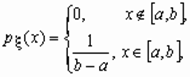
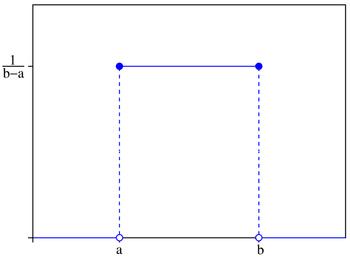
 имеет соответственно вид:
имеет соответственно вид: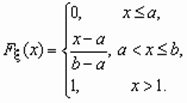
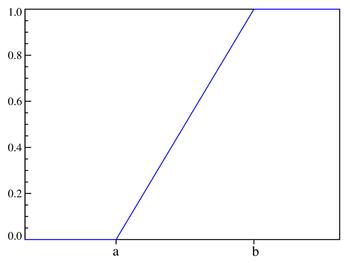
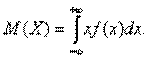
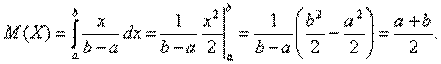
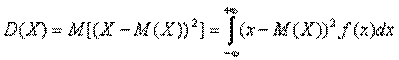

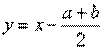 дает возможность записать:
дает возможность записать:
 =
=  =
= 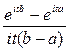
 для нечетного r
для нечетного r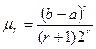 для четного r
для четного r