Распределение Паскаля.
Функция вероятности имеет вид:
Функция распределения не выражается в элементарных функциях.
Параметры: 1. Математическое ожидание
2. Дисперсия
3. Характеристическая функция
8. Медиана нет 9. Мода
Геометрическое распределение. Говорят, что случайная величина
Функция распределения имеет вид:
Параметры:
1.Математическое ожидание M(x)= 2.Дисперсия
3.Характеристическая функция f 8.Медиана нет 9.Мода
Гипергеометрическое распределение. Для гипергеометрического распределения вероятность принятия случайной величиной Y значения y имеет вид:
Функция распределения не выражается в элементарных функциях.
Параметры:
1.Математическое ожидание
2.Дисперсия
3.Характеристическое уравнение
8.Медианы нет 9.Мода
Распределение Пойе. Плотность вероятности случайной величины имеет вид:
где Параметры: 1.Математическое ожидание
2.Дисперсия
|
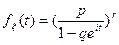
имеет геометрическое распределение с параметром 
, если 
. Случайная величина с таким распределением имеет смысл номера первого успешного испытания в схеме Бернулли с вероятностью успеха p. Таблица распределения 
или 
= 
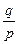
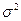(t)= 
, 
, 
