Уравнение  , где y(t), u(t) – соответственно выход и вход звена, K, Т – соответственно коэффициент усиления и постоянная времени.
, где y(t), u(t) – соответственно выход и вход звена, K, Т – соответственно коэффициент усиления и постоянная времени.
Передаточная функция (ПФ) 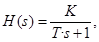
(здесь K– коэффициент усиления, Т – постоянная времени. Свойство: необходимое условие устойчивостиодновременно является и достаточным условием.
Частотная ПФ 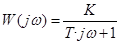
Амплитудно-частотная характеристика (то же самое, что модуль частотной ПФ) определяется формулой 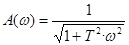
Фазовая частотная характеристика 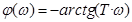
Логарифмическая амплитудная характеристика: (асимптотическая) Начальная часть, до частоты  , аппроксимируется прямой, параллельной абсциссе (значение 20×lg(K), при K= 1 равно 0, т.е. совпадает с абсциссой). При
, аппроксимируется прямой, параллельной абсциссе (значение 20×lg(K), при K= 1 равно 0, т.е. совпадает с абсциссой). При  аппроксимируется прямой с отрицательным наклоном (– 20 Дб/декаду). Т.е. характерными параметрами ЛАЧХ при К =0 являются (0; –20)
аппроксимируется прямой с отрицательным наклоном (– 20 Дб/декаду). Т.е. характерными параметрами ЛАЧХ при К =0 являются (0; –20)
Логарифмическая фазовая характеристика – при изменении частоты изменяется плавно от 0 до (–90°), значение (–45 °) соответствует сопрягающей частоте  .
.
Апериодическое звено 2-го порядка (по сути – последовательное соединение двух апериодических звеньев 1-го порядка с постоянными времени T 1, T 2соответственно).
Уравнение  , где y (t), u (t) – соответственно выход и вход звена, K, Т 1, Т 2 – соответственно коэффициент усиления и постоянные времени.
, где y (t), u (t) – соответственно выход и вход звена, K, Т 1, Т 2 – соответственно коэффициент усиления и постоянные времени.
Передаточная функция (ПФ) 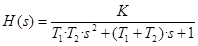
Свойство: необходимое условие устойчивости одновременно является и достаточным условием.
Частотная ПФ 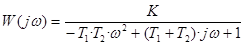
Амплитудно-частотная характеристика (то же самое, что модуль частотной ПФ) определяется формулой 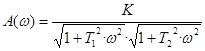
Фазовая частотная характеристика 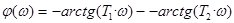
Логарифмическая амплитудная характеристика: (асимптотическая). Без ограничения общности примем, что Т 1 > T 2. Начальная часть, до частоты 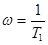 , аппроксимируется прямой, параллельной абсциссе (значение 20×lg(K), при K= 1 равно 0, т.е. совпадает с абсциссой). При
, аппроксимируется прямой, параллельной абсциссе (значение 20×lg(K), при K= 1 равно 0, т.е. совпадает с абсциссой). При  аппроксимируется прямой с отрицательным наклоном (– 20 Дб/декаду). При
аппроксимируется прямой с отрицательным наклоном (– 20 Дб/декаду). При 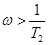 аппроксимируется прямой с отрицательным наклоном (–40 Дб/декаду). Т.е. характерными параметрами ЛАЧХ при К =1 являются наклоны (0; –20; –40), сопрягающие частоты
аппроксимируется прямой с отрицательным наклоном (–40 Дб/декаду). Т.е. характерными параметрами ЛАЧХ при К =1 являются наклоны (0; –20; –40), сопрягающие частоты 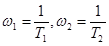
Логарифмическая фазовая характеристика – при изменении частоты изменяется плавно от 0 до (–180°)
Колебательное звено 2-го порядка.
Уравнение  , где y (t), u (t) – соответственно выход и вход звена, K, Т,x – соответственно коэффициент усиления, постоянная времени и коэффициент затухания.
, где y (t), u (t) – соответственно выход и вход звена, K, Т,x – соответственно коэффициент усиления, постоянная времени и коэффициент затухания.
Передаточная функция (ПФ) 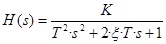
Свойство: необходимое условие устойчивости одновременно является и достаточным условием.
Частотная ПФ 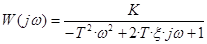
Амплитудно-частотная характеристика (то же самое, что модуль частотной ПФ) определяется формулой 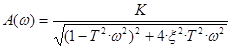
Фазовая частотная характеристика 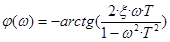
Логарифмическая амплитудная характеристика: При  – параллельна оси абсцисс, равна 20×lg(K). Имеет резонансный пик при
– параллельна оси абсцисс, равна 20×lg(K). Имеет резонансный пик при 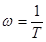 . При
. При  аппроксимируется прямой с отрицательным наклоном (– 40 Дб/декаду). Характерные параметры при K =1: наклоны (0; – 40), изменение наклона на сопрягающей частоте
аппроксимируется прямой с отрицательным наклоном (– 40 Дб/декаду). Характерные параметры при K =1: наклоны (0; – 40), изменение наклона на сопрягающей частоте 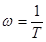
Логарифмическая фазовая характеристика – при изменении частоты изменяется плавно от 0 до (–180°)
Консервативное звено.
Уравнение  , где y(t), u(t) – соответственно выход и вход звена, K, Т – соответственно коэффициент усиления и постоянная времени.
, где y(t), u(t) – соответственно выход и вход звена, K, Т – соответственно коэффициент усиления и постоянная времени.
Передаточная функция (ПФ ) 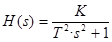
Свойство: звено находится на границе устойчивости колебательного типа (незатухающие колебания с постоянной амплитудой).
Частотная ПФ 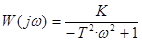
Амплитудно-частотная характеристика (то же самое, что модуль частотной ПФ) определяется формулой  ; имеет разрыв на резонансной частоте
; имеет разрыв на резонансной частоте  .
.
Фазовая частотная характеристика  (ступенчатое изменение при
(ступенчатое изменение при  )
)
Логарифмическая амплитудная характеристика: Имеет разрыв при  . При
. При  аппроксимируется прямой с отрицательным наклоном (– 40 Дб/декаду).
аппроксимируется прямой с отрицательным наклоном (– 40 Дб/декаду).
Логарифмическая фазовая характеристика 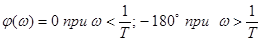
( ступенчатое изменение при  )
)
Интегрирующее звено (идеальное)
Уравнение  , где y(t), u(t) – соответственно выход и вход звена, K –коэффициент усиления.
, где y(t), u(t) – соответственно выход и вход звена, K –коэффициент усиления.
Передаточная функция (ПФ)  (здесь K – коэффициент усиления)
(здесь K – коэффициент усиления)
Частотная ПФ 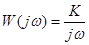
Амплитудно-частотная характеристика (то же самое, что модуль частотной ПФ) определяется формулой 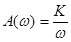 (при w=0 бесконечна, уравнение гиперболы)
(при w=0 бесконечна, уравнение гиперболы)
Фазовая частотная характеристика  (параллельна оси абсцисс)
(параллельна оси абсцисс)
Логарифмическая амплитудная характеристика (асимптотическая):  : до сопрягающей частоты прямая с отрицательным наклоном (–20Дб/декаду). Характерный параметр – наклон (–20).
: до сопрягающей частоты прямая с отрицательным наклоном (–20Дб/декаду). Характерный параметр – наклон (–20).
Логарифмическая фазовая частотная характеристика  (параллельна оси абсцисс).
(параллельна оси абсцисс).
Интегрирующее звено с замедлением (реальное интегрирующее звено)
Уравнение  , где y (t), u (t) – соответственно выход и вход звена, K –коэффициент усиления.
, где y (t), u (t) – соответственно выход и вход звена, K –коэффициент усиления.
Передаточная функция (ПФ)  (здесь K, Т – коэффициент усиления и постоянная времени) сути – последовательное соединение идеального интегрирующего звена и апериодического звена 1-го порядка.
(здесь K, Т – коэффициент усиления и постоянная времени) сути – последовательное соединение идеального интегрирующего звена и апериодического звена 1-го порядка.
Частотная ПФ 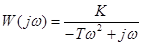
Амплитудно-частотная характеристика (то же самое, что модуль частотной ПФ) определяется формулой  (при w=0 бесконечна)
(при w=0 бесконечна)
Фазовая частотная характеристика 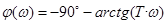
Логарифмическая амплитудная частотная характеристика:  . До сопрягающей частоты
. До сопрягающей частоты 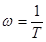 прямая с отрицательным наклоном (–20Дб/декаду). При
прямая с отрицательным наклоном (–20Дб/декаду). При  прямая с отрицательным наклоном (–40Дб/декаду). Характерный параметр – наклоны (–20;–40), сопрягающая частота
прямая с отрицательным наклоном (–40Дб/декаду). Характерный параметр – наклоны (–20;–40), сопрягающая частота 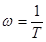
Логарифмическая фазовая частотная характеристика  (сумма сдвигов фаз идеального и апериодического звеньев).
(сумма сдвигов фаз идеального и апериодического звеньев).
Изодромное звено (ПИ-закон управления)
Уравнение  , где y (t), u (t) – соответственно выход и вход звена, K, K 1 –коэффициенты усиления при интегрально й и пропорциональной составляющих звена.
, где y (t), u (t) – соответственно выход и вход звена, K, K 1 –коэффициенты усиления при интегрально й и пропорциональной составляющих звена.
Передаточная функция (ПФ)  (здесь K,
(здесь K,  – коэффициент усиления и постоянная времени) сути – параллельное соединение идеального интегрирующего звена и усилительного (безынерционного) звена 1-го порядка.
– коэффициент усиления и постоянная времени) сути – параллельное соединение идеального интегрирующего звена и усилительного (безынерционного) звена 1-го порядка.
Частотная ПФ 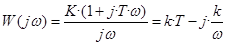
Амплитудно-частотная характеристика (то же самое, что модуль частотной ПФ) определяется формулой 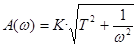
Фазовая частотная характеристика 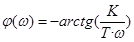 . При w=0 начинается с (–90°), при увеличении частоты плавно стремится к нулю.
. При w=0 начинается с (–90°), при увеличении частоты плавно стремится к нулю.
Логарифмическая амплитудная частотная характеристика (асимптотическая):  . До сопрягающей частоты
. До сопрягающей частоты 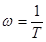 прямая с отрицательным наклоном (–20Дб/декаду). При
прямая с отрицательным наклоном (–20Дб/декаду). При  прямая, параллельная оси абсцисс. Характерный параметр – наклоны (–20;0), сопрягающая частота
прямая, параллельная оси абсцисс. Характерный параметр – наклоны (–20;0), сопрягающая частота 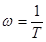
Логарифмическая фазовая частотная характеристика 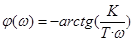 (при w=0 начинается с (–90°), при увеличении частоты плавно стремится к нулю).
(при w=0 начинается с (–90°), при увеличении частоты плавно стремится к нулю).
Дифференцирующее звено (идеальное)
Уравнение  , где y (t), u (t) – соответственно выход и вход звена, K –коэффициент усиления.
, где y (t), u (t) – соответственно выход и вход звена, K –коэффициент усиления.
Передаточная функция (ПФ)  (здесь K – коэффициент усиления)
(здесь K – коэффициент усиления)
Частотная ПФ 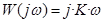
Амплитудно-частотная характеристика (то же самое, что модуль частотной ПФ) определяется формулой  (при w=0 находится в начале координат, при увеличении w проходит через первый квадрант системы координат по прямой под углом, зависящим от значения K. При K = 1– под углом 45°)
(при w=0 находится в начале координат, при увеличении w проходит через первый квадрант системы координат по прямой под углом, зависящим от значения K. При K = 1– под углом 45°)
Фазовая частотная характеристика 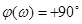 (параллельна оси абсцисс, физический эффект – опережение фазы выхода по отношению ко входу)
(параллельна оси абсцисс, физический эффект – опережение фазы выхода по отношению ко входу)
Логарифмическая амплитудная характеристика (асимптотическая):  : прямая с положительным наклоном (+20Дб/декаду). Характерный параметр – наклон (+20).
: прямая с положительным наклоном (+20Дб/декаду). Характерный параметр – наклон (+20).
Логарифмическая фазовая частотная характеристика 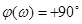 (параллельна оси абсцисс).
(параллельна оси абсцисс).
Дифференцирующее звено с замедлением (реальное дифференцирующее звено)
Уравнение  , где y (t), u (t) – соответственно выход и вход звена; K, Т – соответственно коэффициент усиления и постоянная времени
, где y (t), u (t) – соответственно выход и вход звена; K, Т – соответственно коэффициент усиления и постоянная времени
Передаточная функция (ПФ) 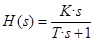 (здесь K,Т – коэффициент усиления и постоянная времени)
(здесь K,Т – коэффициент усиления и постоянная времени)
Частотная ПФ 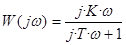
Амплитудно-частотная характеристика (то же самое, что модуль частотной ПФ) определяется формулой  (при w=0 находится в начале координат, при увеличении w проходит через первый квадрант системы координат по плавной кривой с насыщением (т.е. стремится к прямой, параллельной оси абсцисс)
(при w=0 находится в начале координат, при увеличении w проходит через первый квадрант системы координат по плавной кривой с насыщением (т.е. стремится к прямой, параллельной оси абсцисс)
Фазовая частотная характеристика  (при w=0 равна 90°, затем по мере увеличения w плавно спадает до нуля, оставаясь в первом квадранте).
(при w=0 равна 90°, затем по мере увеличения w плавно спадает до нуля, оставаясь в первом квадранте).
Логарифмическая амплитудная характеристика (асимптотическая):  : при малых частотах w – прямая с положительным наклоном (+20Дб/декаду), при
: при малых частотах w – прямая с положительным наклоном (+20Дб/декаду), при  – прямая, параллельная абсциссе. Характерные параметры – наклон (+20;0), сопрягающая частота
– прямая, параллельная абсциссе. Характерные параметры – наклон (+20;0), сопрягающая частота  .
.
Логарифмическая фазовая частотная характеристика  .
.

 , где y(t), u(t) – соответственно выход и вход звена, K, Т – соответственно коэффициент усиления и постоянная времени.
, где y(t), u(t) – соответственно выход и вход звена, K, Т – соответственно коэффициент усиления и постоянная времени.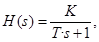
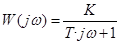
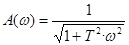
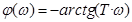
 , аппроксимируется прямой, параллельной абсциссе (значение 20×lg(K), при K= 1 равно 0, т.е. совпадает с абсциссой). При
, аппроксимируется прямой, параллельной абсциссе (значение 20×lg(K), при K= 1 равно 0, т.е. совпадает с абсциссой). При  аппроксимируется прямой с отрицательным наклоном (– 20 Дб/декаду). Т.е. характерными параметрами ЛАЧХ при К =0 являются (0; –20)
аппроксимируется прямой с отрицательным наклоном (– 20 Дб/декаду). Т.е. характерными параметрами ЛАЧХ при К =0 являются (0; –20) , где y (t), u (t) – соответственно выход и вход звена, K, Т 1, Т 2 – соответственно коэффициент усиления и постоянные времени.
, где y (t), u (t) – соответственно выход и вход звена, K, Т 1, Т 2 – соответственно коэффициент усиления и постоянные времени.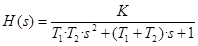
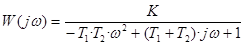
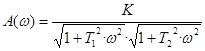
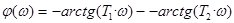
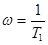 , аппроксимируется прямой, параллельной абсциссе (значение 20×lg(K), при K= 1 равно 0, т.е. совпадает с абсциссой). При
, аппроксимируется прямой, параллельной абсциссе (значение 20×lg(K), при K= 1 равно 0, т.е. совпадает с абсциссой). При  аппроксимируется прямой с отрицательным наклоном (– 20 Дб/декаду). При
аппроксимируется прямой с отрицательным наклоном (– 20 Дб/декаду). При 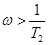 аппроксимируется прямой с отрицательным наклоном (–40 Дб/декаду). Т.е. характерными параметрами ЛАЧХ при К =1 являются наклоны (0; –20; –40), сопрягающие частоты
аппроксимируется прямой с отрицательным наклоном (–40 Дб/декаду). Т.е. характерными параметрами ЛАЧХ при К =1 являются наклоны (0; –20; –40), сопрягающие частоты 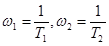
 , где y (t), u (t) – соответственно выход и вход звена, K, Т,x – соответственно коэффициент усиления, постоянная времени и коэффициент затухания.
, где y (t), u (t) – соответственно выход и вход звена, K, Т,x – соответственно коэффициент усиления, постоянная времени и коэффициент затухания.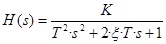
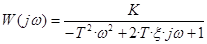
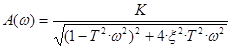
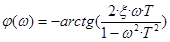
 – параллельна оси абсцисс, равна 20×lg(K). Имеет резонансный пик при
– параллельна оси абсцисс, равна 20×lg(K). Имеет резонансный пик при 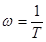 . При
. При  аппроксимируется прямой с отрицательным наклоном (– 40 Дб/декаду). Характерные параметры при K =1: наклоны (0; – 40), изменение наклона на сопрягающей частоте
аппроксимируется прямой с отрицательным наклоном (– 40 Дб/декаду). Характерные параметры при K =1: наклоны (0; – 40), изменение наклона на сопрягающей частоте  , где y(t), u(t) – соответственно выход и вход звена, K, Т – соответственно коэффициент усиления и постоянная времени.
, где y(t), u(t) – соответственно выход и вход звена, K, Т – соответственно коэффициент усиления и постоянная времени.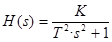
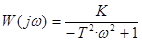
 ; имеет разрыв на резонансной частоте
; имеет разрыв на резонансной частоте  .
. (ступенчатое изменение при
(ступенчатое изменение при  аппроксимируется прямой с отрицательным наклоном (– 40 Дб/декаду).
аппроксимируется прямой с отрицательным наклоном (– 40 Дб/декаду).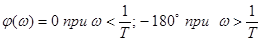
 , где y(t), u(t) – соответственно выход и вход звена, K –коэффициент усиления.
, где y(t), u(t) – соответственно выход и вход звена, K –коэффициент усиления. (здесь K – коэффициент усиления)
(здесь K – коэффициент усиления)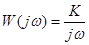
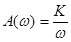 (при w=0 бесконечна, уравнение гиперболы)
(при w=0 бесконечна, уравнение гиперболы) (параллельна оси абсцисс)
(параллельна оси абсцисс) : до сопрягающей частоты прямая с отрицательным наклоном (–20Дб/декаду). Характерный параметр – наклон (–20).
: до сопрягающей частоты прямая с отрицательным наклоном (–20Дб/декаду). Характерный параметр – наклон (–20). , где y (t), u (t) – соответственно выход и вход звена, K –коэффициент усиления.
, где y (t), u (t) – соответственно выход и вход звена, K –коэффициент усиления. (здесь K, Т – коэффициент усиления и постоянная времени) сути – последовательное соединение идеального интегрирующего звена и апериодического звена 1-го порядка.
(здесь K, Т – коэффициент усиления и постоянная времени) сути – последовательное соединение идеального интегрирующего звена и апериодического звена 1-го порядка.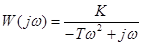
 (при w=0 бесконечна)
(при w=0 бесконечна)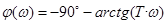
 . До сопрягающей частоты
. До сопрягающей частоты  прямая с отрицательным наклоном (–40Дб/декаду). Характерный параметр – наклоны (–20;–40), сопрягающая частота
прямая с отрицательным наклоном (–40Дб/декаду). Характерный параметр – наклоны (–20;–40), сопрягающая частота  (сумма сдвигов фаз идеального и апериодического звеньев).
(сумма сдвигов фаз идеального и апериодического звеньев). , где y (t), u (t) – соответственно выход и вход звена, K, K 1 –коэффициенты усиления при интегрально й и пропорциональной составляющих звена.
, где y (t), u (t) – соответственно выход и вход звена, K, K 1 –коэффициенты усиления при интегрально й и пропорциональной составляющих звена. (здесь K,
(здесь K,  – коэффициент усиления и постоянная времени) сути – параллельное соединение идеального интегрирующего звена и усилительного (безынерционного) звена 1-го порядка.
– коэффициент усиления и постоянная времени) сути – параллельное соединение идеального интегрирующего звена и усилительного (безынерционного) звена 1-го порядка.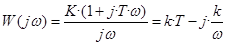
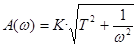
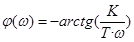 . При w=0 начинается с (–90°), при увеличении частоты плавно стремится к нулю.
. При w=0 начинается с (–90°), при увеличении частоты плавно стремится к нулю. . До сопрягающей частоты
. До сопрягающей частоты 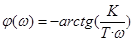 (при w=0 начинается с (–90°), при увеличении частоты плавно стремится к нулю).
(при w=0 начинается с (–90°), при увеличении частоты плавно стремится к нулю). , где y (t), u (t) – соответственно выход и вход звена, K –коэффициент усиления.
, где y (t), u (t) – соответственно выход и вход звена, K –коэффициент усиления. (здесь K – коэффициент усиления)
(здесь K – коэффициент усиления)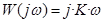
 (при w=0 находится в начале координат, при увеличении w проходит через первый квадрант системы координат по прямой под углом, зависящим от значения K. При K = 1– под углом 45°)
(при w=0 находится в начале координат, при увеличении w проходит через первый квадрант системы координат по прямой под углом, зависящим от значения K. При K = 1– под углом 45°)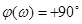 (параллельна оси абсцисс, физический эффект – опережение фазы выхода по отношению ко входу)
(параллельна оси абсцисс, физический эффект – опережение фазы выхода по отношению ко входу) : прямая с положительным наклоном (+20Дб/декаду). Характерный параметр – наклон (+20).
: прямая с положительным наклоном (+20Дб/декаду). Характерный параметр – наклон (+20). , где y (t), u (t) – соответственно выход и вход звена; K, Т – соответственно коэффициент усиления и постоянная времени
, где y (t), u (t) – соответственно выход и вход звена; K, Т – соответственно коэффициент усиления и постоянная времени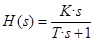 (здесь K,Т – коэффициент усиления и постоянная времени)
(здесь K,Т – коэффициент усиления и постоянная времени)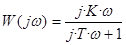
 (при w=0 находится в начале координат, при увеличении w проходит через первый квадрант системы координат по плавной кривой с насыщением (т.е. стремится к прямой, параллельной оси абсцисс)
(при w=0 находится в начале координат, при увеличении w проходит через первый квадрант системы координат по плавной кривой с насыщением (т.е. стремится к прямой, параллельной оси абсцисс) (при w=0 равна 90°, затем по мере увеличения w плавно спадает до нуля, оставаясь в первом квадранте).
(при w=0 равна 90°, затем по мере увеличения w плавно спадает до нуля, оставаясь в первом квадранте). : при малых частотах w – прямая с положительным наклоном (+20Дб/декаду), при
: при малых частотах w – прямая с положительным наклоном (+20Дб/декаду), при  – прямая, параллельная абсциссе. Характерные параметры – наклон (+20;0), сопрягающая частота
– прямая, параллельная абсциссе. Характерные параметры – наклон (+20;0), сопрягающая частота  .
.


