Качество управления
Определение: показатели качества управления – это субъективные характеристики процессов в САУ, зависящие от требований Заказчика и от опыта проектировщика САУ (в отличие от объективных характеристик – например, устойчивости). Группы показателей качества – характеризующие: 1) точность; 2) быстродействие; 3) степень устойчивости; 4) комплексно – все три вида показателей. Способы определения: 1) – непосредственно по обработке данных о реакциях САУ на типовые воздействия (прямые показатели качества); 2) по косвенным данным (по частотным характеристикам, расположению корней <знаменатель ПФ=0>; по корневым годографам…)
Прямые показатели (оцениваются непосредственно по графику изменения выхода во времени) На рис. – типичный переходный процесс отработки ненулевых начальных условий при внешних воздействиях = 0.
А) Показатели, характеризующие свободную составляющую процесса на выходе САУ 1) Время переходного процесса
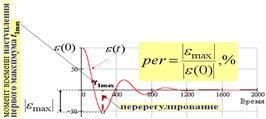
2) Перерегулирование и наступление 1-го максимума
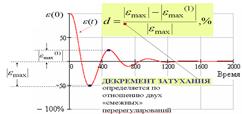
3) Декремент затухания
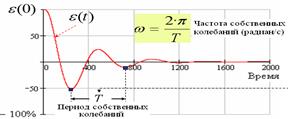
4) Частота и период собственных колебаний
5) Число полных колебаний
Б) Показатели, характеризующие вынужденную составляющую процесса на выходе САУ 1) Статическая ошибка
2 ) Динамическая ошибка
3) Астатизм, порядок астатизма Определение: САУ, замкнутая обратной связью, обладает астатизмом k- го порядка, если в прямой цепи соответствующей ей разомкнутой САУ содержится сомножитель pk (иными словами, в структуре разомкнутой САУ имеется цепь из k интегрирующих звеньев, включенных последовательно). Частные случаи: а) при астатизме 1-го порядка постоянные задающие воздействия воспроизводятся без ошибки (отсутствует статическая ошибка). При переменных задающих воздействиях имеется ненулевая динамическая ошибка. б) При астатизме 2-го порядка постоянные и линейно зависящие от времени задающие воздействия воспроизводятся без ошибки. При задающих воздействиях, зависимость от времени которых отличается от линейной, имеется ненулевая динамическая ошибка. в). При астатизме 3-го порядка постоянные, линейно и квадратично зависящие от времени задающие воздействия воспроизводятся без ошибки. При задающих воздействиях, зависимость от времени которых более сложна, чем квадратичная, имеется динамическая ошибка.
Здесь С 0, С 1,…, Сm – коэффициенты ошибок, вычисляются по передаточной функции (ПФ) по каналу «задающее воздействие g (t) – рассогласование e (t) между задающим воздействием и выходом САУ» и по производным этой ПФ при s =0 (это соответствует t ®¥):
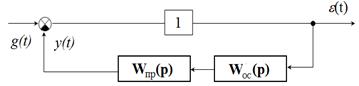
ПФ по каналу «задающее воздействие g (t) – рассогласование e (t)» вычисляется по формуле:
Здесь W пр(s), WОС (s) – соответственно ПФ прямой цепи и цепи обратной связи.
Вычисления проиллюстрируем примером. Пусть задающее воздействие линейно зависит от времени:
Требуется найти установившееся значение ошибки e уст(t) при этом задающем воздействии. Задана передаточная функция разомкнутой САУ (ПФ прямой цепи), она равна Шаг 1. Рассчитываем передаточную функцию САУ по каналу «задающее воздействие – рассогласование».
Соответствующая ПФ равна:
В примере W ОС(s) =1, Шаг 2. Рассчитываем коэффициенты ошибок. Для рассматриваемого примера нужна только первая производная ПФ Wge(s) при s=0: старшие производные не потребуются, т.к. все производные задающего воздействия в примере выше первой равны нулю. После вычисления полагаем s = 0. Получим коэффициенты ошибок:
Шаг 3. Рассчитываем первую производную задающего воздействия:
Шаг 4. Пользуясь формулой с коэффициентами ошибок, находим: установившееся значение рассогласования e (t) между задающим воздействием и выходом задающим воздействием и выходом задающим воздействием и выходом задающим воздействием и выходом равно:
Косвенные показатели качества А) Показатели, оцениваемые по распределению корней характеристического уравнения <знаменатель передаточной функции замкнутой САУ = 0>: Время переходного процесса, Колебательность, Затухание – см. рис. ниже
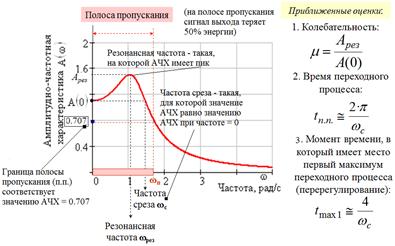
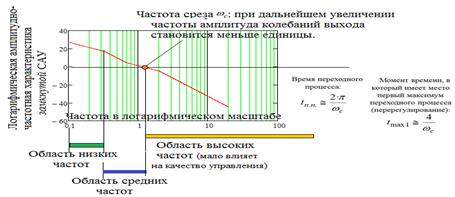
Б) Показатели, оцениваемые по амплитудно-частотной характеристике замкнутой САУ: Частота среза, Полоса пропускания, Резонансная частота, Колебательность, Время переходного процесса, Момент времени наступления первого максимума – см. рисунок ниже
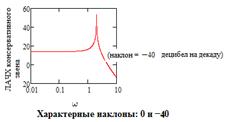
В) Показатели, оцениваемые по логарифмической амплитудно-частотной характеристике разомкнутой САУ: частота среза; время переходного процесса; момент времени, при котором наступает перерегулирование.
Примеры с ЛАЧХ, включенные в тест Минобразования: 1)Среднечастотная часть логарифмической амплитудно-частотной характеристики определяет… (из формулы, показанной на рисунке выше, ясен ответ: время переходного процесса и перерегулирование) 2)
Передаточные функции (ПФ)
Относительной степенью передаточной функции называется РАЗНОСТЬ СТЕПЕНЕЙ ЗНАМЕНАТЕЛЯ И ЧИСЛИТЕЛЯ передаточной функции Построение передаточной функции по дифференциальному уравнению, пример. Задание: построить ПФ по уравнению Решение: ПФ имеет форму дроби (в лекциях обозначали W, в тестах обозначена H), используется оператор Лапласа (в лекциях обозначали p, в тестах обозначение s). По определению ПФ есть отношение изображения (по Лапласу) выхода объекта к изображению входа. Построение ПФ: в числителе – многочлен s правой части уравнения, степени элементов многочлена соответствуют порядку производной. В примере числитель: s + 5. В знаменателе – аналогичный многочлен левой части. В примере: s2 + 2. ВНИМАНИЕ: не записывайте s0 при элементах уравнения, не являющихся производными. Ответ в примере: Частотные характеристики (амплитудно-частотная, логарифмическая) Построение: Шаг 1. Получить частотную передаточную функцию по обычной передаточной функции. Частотная передаточная функция строится по передаточной функции H(s) путем замены оператора s на комплексный аргумент (jw) (здесь Амплитудно-частотная характеристика (АЧХ) – это зависимость амплитуды выхода САУ от частоты w единичного синусоидального сигнала, поступающего на вход. Для построения АЧХ необходимо найти модуль частотной передаточной функции (для чего нужно разделить частотную ПФ на действительную и мнимую части и найти зависимость корня квадратного от суммы квадратов этих частей от частоты). Пример: Если Фазовая частотная характеристика (ФЧХ) – это зависимость сдвига фазы выхода САУ по отношению к входу САУ от частоты w единичного синусоидального сигнала, поступающего на вход. Для построения ФЧХ необходимо разделить частотную ПФ на действительную и мнимую части и вычислить арктангенс отношения мнимой части к действительной. Пример: Если Логарифмическая амплитудно-частотная характеристика (ЛАЧХ). Определение: ЛАЧХ – это зависимость десятичного логарифма амплитудно-частотной характеристики A(w) от частоты w (измеряется в децибелах, Дб, шкала ординаты 20Дб). Из соображений масштаба формулу записывают так: Построение ЛАЧХ. Используется аппроксимация ЛАЧХ асимптотическими прямыми линиями. Пример: пусть разомкнутая САУ состоит из последовательного соединения звеньев:
Расположение звеньев – в порядке убывания постоянных времени (только для удобства объяснения; порядок звеньев в последовательной цепи безразличен). Пусть Поскольку амплитудно-частотная характеристика (АЧХ) последовательно соединенных звеньев = произведению АЧХ каждого звена, логарифмическая АЧХ (ЛАЧХ) будет равна сумме ЛАЧХ каждого звена. Асимптотические ЛАЧХ всех звеньев описаны в разделе «Звенья САУ». Строим асимптотические ЛАЧХ каждого звена и суммируем. Масштаб по оси абсцисс – логарифмический, по оси ординат 0 обычный.
ЛАЧХ цепи в целом представляет собой отрезки, соединяющиеся по сопрягающим частотам: Характерные элементы ЛАЧХ (см. также логарифмические характеристики элементарных звеньев): 1) Пересекает ось ординат в точке 20×lg(K), где K – коэффициент усиления САУ (его можно найти по передаточной функции, полагая в частотной передаточной функции частоту w =0 или в обычной ПР полагая s = 0). 2) Апериодическое звено 1-го порядка (ПФ
3) Интегрирующее звено (ПФ
4) Дифференцирующее звено (ПФ
5) Консервативное звено (ПФ
|





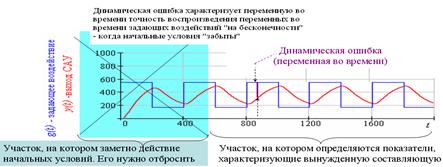
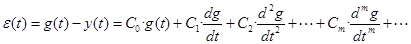 4) Коэффициенты ошибок. Позволяют получить значение рассогласования между гладким (т.е. дифференцируемым сколько угодно раз и поэтому допускающим разложение по степеням) задающим воздействием и выходом САУ «на бесконечности» (т.е. когда САУ «забыла» начальные условия). Общая формула:
4) Коэффициенты ошибок. Позволяют получить значение рассогласования между гладким (т.е. дифференцируемым сколько угодно раз и поэтому допускающим разложение по степеням) задающим воздействием и выходом САУ «на бесконечности» (т.е. когда САУ «забыла» начальные условия). Общая формула: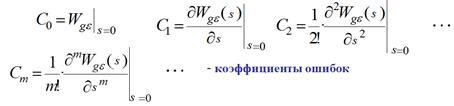
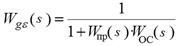
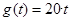
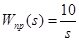 .
.
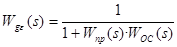
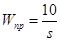 ,
, 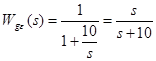 .
.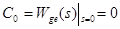 (это означает, что если бы задающее воздействие содержало константу, то она была бы воспроизведена выходом САУ без ошибки: статическая ошибка отсутствует).
(это означает, что если бы задающее воздействие содержало константу, то она была бы воспроизведена выходом САУ без ошибки: статическая ошибка отсутствует). 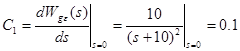
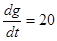
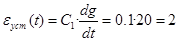 Это и будет решением данного примера.
Это и будет решением данного примера.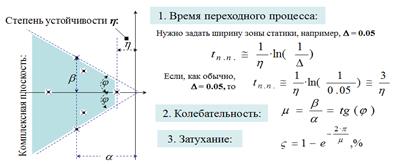
 …
…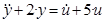 . Здесь обозначено: y(t) – выход, u(t) – вход системы управления в функции времени t.
. Здесь обозначено: y(t) – выход, u(t) – вход системы управления в функции времени t.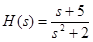
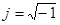 – мнимая единица, w – частота). Пример: пусть передаточная функция САУ равна
– мнимая единица, w – частота). Пример: пусть передаточная функция САУ равна 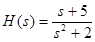 В. Заменяем:
В. Заменяем: 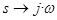 . Получим частотную передаточную функцию
. Получим частотную передаточную функцию 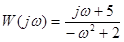 . Шаг 2. Получить действительную и мнимую частотные характеристики (ЧХ). Разделяем W(jw) на сумму действительной и мнимой части. Если в знаменателе есть комплексное слагаемое – нужно умножить и числитель, и знаменатель на выражение, комплексно-сопряженное к знаменателю. В примере знаменатель не содержит комплексного слагаемого. Получим:
. Шаг 2. Получить действительную и мнимую частотные характеристики (ЧХ). Разделяем W(jw) на сумму действительной и мнимой части. Если в знаменателе есть комплексное слагаемое – нужно умножить и числитель, и знаменатель на выражение, комплексно-сопряженное к знаменателю. В примере знаменатель не содержит комплексного слагаемого. Получим: 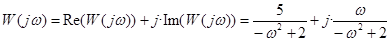 , здесь Re(…) Im(…) – соответственно действительная и мнимая ЧХ. Шаг 3. Получить амплитудно-частотную и фазовую частотную ЧХ. Для этого используется формула Эйлера, позволяющая получить: вместо
, здесь Re(…) Im(…) – соответственно действительная и мнимая ЧХ. Шаг 3. Получить амплитудно-частотную и фазовую частотную ЧХ. Для этого используется формула Эйлера, позволяющая получить: вместо 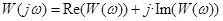 эквивалентное выражение
эквивалентное выражение 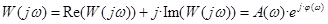 . Здесь
. Здесь 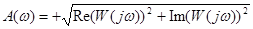 - амплитудно-частотная характеристика. В примере
- амплитудно-частотная характеристика. В примере 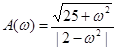 .
. 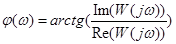 - фазовая частотная характеристика. В примере
- фазовая частотная характеристика. В примере 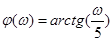 .
. , то вычисляем:
, то вычисляем:  . АФХ равна:
. АФХ равна: 
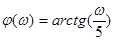
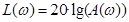 . Ось абсцисс – в логарифмическом масштабе, поэтому ось ординат нельзя провести для w = 0 (нуль не имеет логарифма). Эту ось проводят произвольно. ЛАХ принято аппроксимировать отрезками прямых линий.
. Ось абсцисс – в логарифмическом масштабе, поэтому ось ординат нельзя провести для w = 0 (нуль не имеет логарифма). Эту ось проводят произвольно. ЛАХ принято аппроксимировать отрезками прямых линий.
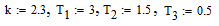


 . Общая идея: пока частота меньше сопрягающей, значением частоты можно пренебречь; если частота больше сопрягающей, то можно пренебречь единицей по сравнению со слагаемым, содержащим частоту в качестве сомножителей.
. Общая идея: пока частота меньше сопрягающей, значением частоты можно пренебречь; если частота больше сопрягающей, то можно пренебречь единицей по сравнению со слагаемым, содержащим частоту в качестве сомножителей. , где K,T – соответственно коэффициент усиления и постоянная времени) имеет асимптотическую ЛАЧХ с наклонами (0 и –20 Дб/декаду)
, где K,T – соответственно коэффициент усиления и постоянная времени) имеет асимптотическую ЛАЧХ с наклонами (0 и –20 Дб/декаду)
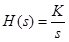 ) имеет ЛАЧХ в виде нисходящей прямой линии с наклоном (– 20 Дб/декаду)
) имеет ЛАЧХ в виде нисходящей прямой линии с наклоном (– 20 Дб/декаду)
 ) имеет ЛАЧХ в виде восходящей прямой линии с наклоном (+ 20 Дб/декаду)
) имеет ЛАЧХ в виде восходящей прямой линии с наклоном (+ 20 Дб/декаду)
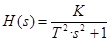 ) имеет ЛАЧХ с разрывом на частоте w=1/T. Характерные наклоны: 0 до частоты разрыва и (–40 Дб/декаду) после частоты разрыва:
) имеет ЛАЧХ с разрывом на частоте w=1/T. Характерные наклоны: 0 до частоты разрыва и (–40 Дб/декаду) после частоты разрыва: