Устойчивость дискретной системы
Шаг 1. Нужно записать уравнение дискретной САУ в форме
Граница устойчивости нейтрального типа имеет место, если все корни характеристического уравнения – внутри единичного круга, кроме единственного, находящегося на действительной оси комплексной плоскости в точке пересечения с окружностью единичного радиуса. В системе, находящейся на границе устойчивости нейтрального типа, выход объекта после снятия внешнего воздействия не возвращается в нуль, но и не уходит в бесконечность.
Граница устойчивости колебательного типа имеет место, если все корни характеристического уравнения – внутри единичного круга, кроме пары корней, лежащих на окружности единичного радиуса (не в точке пересечения с действительной осью). В системе, находящейся на границе устойчивости колебательного типа, выход объекта после снятия внешнего воздействия периодически изменяет знак дискретного сигнала (аналог незатухающих колебаний в непрерывных системах).
К примерам из тестов Минвуза об устойчивости дискретных систем
Пример: уравнение динамики САУ Пример из тестов Минвуза: В замкнутой системе, описываемой разностным уравнением Установившееся значение выхода дискретной САУ при постоянном входном воздействии. Задача имеет смысл только для устойчивой системы. Для расчета нужно положить
|

 (можно принять внешнее воздействие = 0, т.к. факт устойчивости – внутреннее свойство системы, от внешнего воздействия не зависит). Шаг 2. Найти корни характеристического уравнения
(можно принять внешнее воздействие = 0, т.к. факт устойчивости – внутреннее свойство системы, от внешнего воздействия не зависит). Шаг 2. Найти корни характеристического уравнения (корни могут быть действительными и/или попарно комплексно-сопряженными, общее число корней k). Шаг 3. Установить факт устойчивости по теореме: в устойчивой дискретной САУ все корни должны лежать внутри круга единичного радиуса на комплексной плоскости: т.е. для всех qi, i = 1,…, k
(корни могут быть действительными и/или попарно комплексно-сопряженными, общее число корней k). Шаг 3. Установить факт устойчивости по теореме: в устойчивой дискретной САУ все корни должны лежать внутри круга единичного радиуса на комплексной плоскости: т.е. для всех qi, i = 1,…, k  . Здесь Re(…), Im(…) – соответственно действительная и мнимая часть корня. Если хотя бы для одного корня
. Здесь Re(…), Im(…) – соответственно действительная и мнимая часть корня. Если хотя бы для одного корня  , САУ неустойчива. ВНИМАНИЕ: в отличие от систем с непрерывным временем анализ устойчивости НЕ ориентируется на знак вещественной части корней!
, САУ неустойчива. ВНИМАНИЕ: в отличие от систем с непрерывным временем анализ устойчивости НЕ ориентируется на знак вещественной части корней!



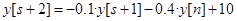 , в нем внешнее воздействие (=10) при анализе устойчивости не учитывается. Характеристическое уравнение:
, в нем внешнее воздействие (=10) при анализе устойчивости не учитывается. Характеристическое уравнение:  . Корни
. Корни  система устойчива.
система устойчива. , где Т – период квантования, n= 0,1,… – дискретное время, g(…) –входная переменная, y(…) – выходная переменная, найти корень характеристического уравнения. Решение: корень находится из уравнения q – 0.2 = 0, т.е. q = 0.2.
, где Т – период квантования, n= 0,1,… – дискретное время, g(…) –входная переменная, y(…) – выходная переменная, найти корень характеристического уравнения. Решение: корень находится из уравнения q – 0.2 = 0, т.е. q = 0.2. и решить соответствующее алгебраическое уравнение относительно установившегося значение выхода y уст. Пример: уравнение динамики САУ
и решить соответствующее алгебраическое уравнение относительно установившегося значение выхода y уст. Пример: уравнение динамики САУ  , получим
, получим  , отсюда
, отсюда 



