Дискретные системы
Модели дискретных линейных систем класса «скалярный вход u [ n ] – скалярный выход y [ n ]» задаются обычно в форме разностных уравнений, связывающих значение выхода объекта на некотором такте со значениями выхода объекта в предшествующих тактах (инерционность) и входа в этом же такте и нескольких предшествующих тактах. Продолжительность такта T – постоянна, такт с номером n соответствует моменту времени (nT). В промежутках между тактами значения входа и выхода не рассматриваются. Пример 1 модели в общем виде (определение текущего значения выхода по предыстории). В примере видно, что значение выхода y [ n ] зависит от предшествующих значений выхода в тактах [ n– 1], [ n– 2],…, [ n–M ] и от управляющих воздействий в тактах [ n– 1], [ n– 2],…, [ n–R ]. Параметрами модели являются коэффициенты ai, i =1,…, M и bk, k = 1,.., R. Обычно R<M, гораздо реже R=M, почти никогда R>M Порядок модели дискретной системы определяется значением M. Модель 1-го порядка: Модель 2-го порядка: Пример 2 модели в общем виде (расчет будущего значения выхода по текущему значению)
Модель 1-го порядка: Модель 2-го порядка: Пример из теста Минвуза: определить порядок разностного уравнения
|
.
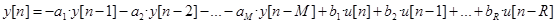Порядок модели дискретной системы определяется значением M.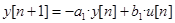
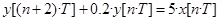, где T – период квантования, n = 0,1,… – дискретное время (такты). Ответ: порядок равен 2.
