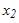Состоятельность оценок параметров регрессии означает, что …

|
|
| точность оценок выборки увеличивается с увеличением объема выборки
|
|
|
|
| математическое ожидание остатков равно нулю
|
|
|
|
| дисперсия остатков минимальная
|
|
|
|
| дисперсия остатков не зависит от величины 
|
Решение:
Состоятельность оценок параметров регрессии означает, что точность оценок выборки увеличивается с увеличением объема выборки.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 60.
 ЗАДАНИЕ N 2 сообщить об ошибке
ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Оценка параметров линейных уравнений регрессии
При методе наименьших квадратов параметры уравнения парной линейной регрессии  определяются из условия ______ остатков
определяются из условия ______ остатков  .
.

|
|
| минимизации суммы квадратов
|
|
|
|
| равенства нулю суммы квадратов
|
|
|
|
| минимизации модулей
|
|
|
|
| равенства нулю
|
Решение:
При методе наименьших квадратов параметры уравнения парной линейной регрессии  определяются из условия минимизации суммы квадратов остатков
определяются из условия минимизации суммы квадратов остатков  .
.
Эконометрика. Краткий курс: учеб. пособие / С.А. Айвазян, С.С. Иванова. – М.: Маркет ДС, 2007. – С.59–61.
 ЗАДАНИЕ N 3 сообщить об ошибке
ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Предпосылки МНК, методы их проверки
Известно, что коэффициент автокорреляции остатков первого порядка равен –0,3. Также даны критические значения статистики Дарбина – Уотсона для заданного количества параметров при неизвестном и количестве наблюдений  ,
,  . По данным характеристикам можно сделать вывод о том, что …
. По данным характеристикам можно сделать вывод о том, что …

|
|
| автокорреляция остатков отсутствует
|
|
|
|
| статистика Дарбина – Уотсона попадает в зону неопределенности
|
|
|
|
| есть положительная автокорреляция остатков
|
|
|
|
| есть отрицательная автокорреляция остатков
|
Решение:
Дано, что коэффициент автокорреляции остатков первого порядка равен –0,3,  . Рассчитаем статистику Дарбина – Уотсона по формуле
. Рассчитаем статистику Дарбина – Уотсона по формуле  . Нам известны критические значения статистики Дарбина – Уотсона для заданного количества параметров при неизвестном и количестве наблюдений
. Нам известны критические значения статистики Дарбина – Уотсона для заданного количества параметров при неизвестном и количестве наблюдений  ,
,  , которые разбивают отрезок от 0 до 4 на пять частей.
, которые разбивают отрезок от 0 до 4 на пять частей.
В интервале [0; 0,82] есть положительная автокорреляция остатков;
в интервале (0,82; 1,32] – зона неопределенности;
в интервале (1,32; 2,68] нет автокорреляции остатков;
в интервале (2,68; 3,12] – зона неопределенности;
в интервале (3,12; 4] есть отрицательная автокорреляция остатков.
В нашем случае значение статистики Дарбина–Уотсона d=2,6 попадает в интервал (1,32; 2,68]. Значит, можно сделать вывод, что нет автокорреляции остатков.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С.438-442, 186-197.
Бывшев В.А. Эконометрика: учеб. пособие / В.А. Бывшев. – М.: Финансы и статистика, 2008. – С.268–301.
 ЗАДАНИЕ N 4 сообщить об ошибке
ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Обобщенный метод наименьших квадратов (ОМНК)
Для оценки параметров регрессионной модели с коррелированными остатками используется _______ метод наименьших квадратов.

|
|
| обобщенный
|
|
|
|
| традиционный
|
|
|
|
| двухшаговый
|
|
|
|
| косвенный
|
Решение:
Метод наименьших квадратов (МНК) позволяет рассчитать такие оценки параметров линейной модели регрессии, для которых сумма квадратов отклонений фактических значений зависимой переменной y от ее модельных (теоретических) значений  минимальна. Отклонение
минимальна. Отклонение  , посчитанное для i -го наблюдения, является ошибкой модели. При применении МНК относительно остатков регрессионной модели выдвигаются определенные предпосылки: случайный характер остатков, нулевая средняя величина, отсутствие автокорреляции в остатках, постоянная дисперсия (гомоскедастичность) остатков, подчинение нормальному закону распределения. Если остатки не удовлетворяют предпосылкам МНК, то применение обычного (традиционного) МНК нецелесообразно. Если остатки автокоррелированны и/или гетероскедастичны, то проводят преобразование переменных и расчет оценок параметров осуществляют с использованием обобщенного метода наименьших квадратов (ОМНК). Верным вариантом является «обобщенный».
, посчитанное для i -го наблюдения, является ошибкой модели. При применении МНК относительно остатков регрессионной модели выдвигаются определенные предпосылки: случайный характер остатков, нулевая средняя величина, отсутствие автокорреляции в остатках, постоянная дисперсия (гомоскедастичность) остатков, подчинение нормальному закону распределения. Если остатки не удовлетворяют предпосылкам МНК, то применение обычного (традиционного) МНК нецелесообразно. Если остатки автокоррелированны и/или гетероскедастичны, то проводят преобразование переменных и расчет оценок параметров осуществляют с использованием обобщенного метода наименьших квадратов (ОМНК). Верным вариантом является «обобщенный».
 ЗАДАНИЕ N 5 сообщить об ошибке
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Проверка статистической значимости эконометрической модели
При оценке статистической значимости построенной эконометрической модели выдвигают ______ гипотезы.

|
|
| статистические
|
|
|
|
| математические
|
|
|
|
| информационные
|
|
|
|
| коллективные
|
Решение:
Эконометрическая модель дает количественное выражение некоторой исследуемой зависимости между социально-экономическими показателями. При этом оценка параметров модели осуществляется по некоторой статистической выборке, отражающей данную зависимость для генеральной совокупности однородных объектов. Поэтому при проверке статистической значимости модели выдвигаются статистические гипотезы: нулевую H0 и альтернативную Н1.
 ЗАДАНИЕ N 6 сообщить об ошибке
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Оценка тесноты связи
Коэффициент корреляции  парной линейной регрессии
парной линейной регрессии  нельзя рассчитать по формуле …
нельзя рассчитать по формуле …
 ЗАДАНИЕ N 7 сообщить об ошибке
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Оценка качества подбора уравнения
Если общая сумма квадратов отклонений  , и остаточная сумма квадратов отклонений
, и остаточная сумма квадратов отклонений  , то сумма квадратов отклонений, объясненная регрессией, равна …
, то сумма квадратов отклонений, объясненная регрессией, равна …

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0,25
|
 ЗАДАНИЕ N 8 сообщить об ошибке
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Оценка значимости параметров эконометрической модели
Если параметр эконометрической модели не является статистически значимым, то соответствующая независимая переменная …

|
|
| не оказывает влияния на моделируемый показатель (зависимую переменную)
|
|
|
|
| оказывает статистически значимое влияние на моделируемый показатель (зависимую переменную)
|
|
|
|
| тесно связан с зависимой переменной
|
|
|
|
| оказывает основное (доминирующее) влияние на зависимую переменную
|
 ЗАДАНИЕ N 9 сообщить об ошибке
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Фиктивные переменные
При исследовании зависимости потребления мяса от уровня дохода и пола потребителя можно рекомендовать …

|
|
| использовать фиктивную переменную – пол потребителя
|

|
|
| разделить совокупность на две: для потребителей женского пола и для потребителей мужского пола
|
|
|
|
| использовать фиктивную переменную – уровень дохода
|
|
|
|
| исключить из рассмотрения пол потребителя, так как данный фактор нельзя измерить количественным образом
|
Решение:
При построении регрессионной модели может возникнуть ситуация, когда необходимо включить в уравнение помимо количественных переменных переменные, отражающие некоторые атрибутивные признаки (пол, образование, регион и т.п.). Такого рода качественные переменные называются «фиктивными» (dummy) переменными. Они отражают неоднородность исследуемой статистической совокупности и используются для более качественного моделирования зависимостей в таких неоднородных объектах наблюдения. При моделировании отдельных зависимостей по неоднородным данным можно также воспользоваться способом разделения всей совокупности неоднородных данных на несколько отдельных совокупностей, количество которых равно количеству состояний dummy-переменной. Таким образом правильными вариантами ответов являются: «использовать фиктивную переменную – пол потребителя» и «разделить совокупность на две: для потребителей женского пола и для потребителей мужского пола».
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С. 121–127.
 ЗАДАНИЕ N 10 сообщить об ошибке
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Спецификация эконометрической модели
Эконометрическая модель уравнения регрессии может включать одну или несколько независимых переменных. По данному классификационному признаку различают _______ регрессию.

|
|
| простую и множественную
|
|
|
|
| линейную и нелинейную
|
|
|
|
| множественную и многофакторную
|
|
|
|
| простую и парную
|
Решение:
Эконометрическая модель уравнения регрессии может быть представлена выражением  , где y – зависимая переменная, xj – независимая переменная (j = 1,…, k; k – количество независимых переменных), f – тип функциональной зависимости (математическая функция),
, где y – зависимая переменная, xj – независимая переменная (j = 1,…, k; k – количество независимых переменных), f – тип функциональной зависимости (математическая функция),  – случайные факторы. Спецификация эконометрической модели уравнения регрессии определяется видом функции f, а также числом независимых переменных (факторов или регрессоров). Парная и множественная регрессия характеризуют количество независимых переменных хj в уравнении регрессии (парная – одна независимая переменная; множественная – не меньше двух независимых переменных). Поэтому верным вариантом является «простую и множественную» регрессии. Вариант ответа «линейную и нелинейную» – неверный, так как это характеризует вид зависимости (математической функции) f. Варианты «множественную и многофакторную» и «простую и парную» отражают один из классификационных признаков и не описывают всей совокупности эконометрических моделей регрессии.
– случайные факторы. Спецификация эконометрической модели уравнения регрессии определяется видом функции f, а также числом независимых переменных (факторов или регрессоров). Парная и множественная регрессия характеризуют количество независимых переменных хj в уравнении регрессии (парная – одна независимая переменная; множественная – не меньше двух независимых переменных). Поэтому верным вариантом является «простую и множественную» регрессии. Вариант ответа «линейную и нелинейную» – неверный, так как это характеризует вид зависимости (математической функции) f. Варианты «множественную и многофакторную» и «простую и парную» отражают один из классификационных признаков и не описывают всей совокупности эконометрических моделей регрессии.
 ЗАДАНИЕ N 11 сообщить об ошибке
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Линейное уравнение множественной регрессии
В эконометрической модели линейного уравнения множественной регрессии  величина параметра а характеризует среднее по совокупности значение зависимой переменной, при значениях ___, равных 0.
величина параметра а характеризует среднее по совокупности значение зависимой переменной, при значениях ___, равных 0.

|
|
| xj
|
|
|
|
| 
|
|
|
|
| y
|
|
|
|
| a
|
Решение:
Эконометрическая модель линейного уравнения регрессии имеет вид:  , где y – зависимая переменная, xj – независимая переменная (
, где y – зависимая переменная, xj – независимая переменная ( – номер независимой переменной в модели, k – общее количество независимых переменных в модели); a, bj – параметры уравнения;
– номер независимой переменной в модели, k – общее количество независимых переменных в модели); a, bj – параметры уравнения;  – ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Значение зависимой переменной y равно величине параметра а, если все значения независимых переменных xj = 0. Поэтому верным ответом является «хj».
– ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Значение зависимой переменной y равно величине параметра а, если все значения независимых переменных xj = 0. Поэтому верным ответом является «хj».
 ЗАДАНИЕ N 12 сообщить об ошибке
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Отбор факторов, включаемых в модель множественной регрессии
Строится эконометрическая модель уравнения множественной регрессии для зависимости y от пяти факторов х(1), х(2), х(3), х(4), х(5). Получена матрица парных коэффициентов линейной корреляции (y – зависимая переменная):
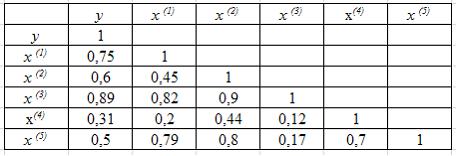
Требование отсутствия коллинеарных независимых переменных выполняется в модели …
Решение:
При построении модели множественной регрессии необходимо исключить возможность существования тесной линейной зависимости между независимыми (объясняющими) переменными, что ведет к проблеме мультиколлинеарности. При этом осуществляют проверку коэффициентов линейной корреляции для каждой пары объясняющих переменных. Эти значения отражены в матрице парных коэффициентов линейной корреляции. Считается, что наличие значений коэффициентов парной корреляции между объясняющими переменными, превышающих по абсолютной величине 0,7, отражает тесную связь между этими переменными (теснота связи с переменной y в данном случае не рассматривается). Такие объясняющие переменные называются коллинеарными, они не должны включаться в одно уравнение. Верным вариантом ответа является « ». Другие варианты ответов являются неверными, так как включают в одно уравнение коллинеарные объясняющие переменные.
». Другие варианты ответов являются неверными, так как включают в одно уравнение коллинеарные объясняющие переменные.
 ЗАДАНИЕ N 13 сообщить об ошибке
ЗАДАНИЕ N 13 сообщить об ошибке
Тема: Виды нелинейных уравнений регрессии
Уравнением нелинейной регрессии, линейной по параметрам является …
Решение:
Рассмотрим каждую из моделей. Уравнение  является нелинейным как по параметрам, так и по переменным. Уравнение
является нелинейным как по параметрам, так и по переменным. Уравнение  является нелинейным по переменной х, но линейным по параметрам. Уравнения
является нелинейным по переменной х, но линейным по параметрам. Уравнения  и
и  также являются нелинейными по переменной х, но линейными по параметрам. Поэтому правильный вариант ответа – «
также являются нелинейными по переменной х, но линейными по параметрам. Поэтому правильный вариант ответа – « ». Другие модели не удовлетворяют поставленному условию.
». Другие модели не удовлетворяют поставленному условию.
 ЗАДАНИЕ N 14 сообщить об ошибке
ЗАДАНИЕ N 14 сообщить об ошибке
Тема: Нелинейные зависимости в экономике
Уравнением нелинейной регрессии, отражающей полиномиальную зависимость y от x, является …
 ЗАДАНИЕ N 15 сообщить об ошибке
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Линеаризация нелинейных моделей регрессии
При линеаризации нелинейных регрессионных моделей как один из видов преобразований используется логарифмирование уравнения. Указанным способом не может быть линеаризовано уравнение …
 ЗАДАНИЕ N 16 сообщить об ошибке
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Оценка качества нелинейных уравнений регрессии
Для нелинейного уравнения регрессии рассчитано значение индекса детерминации 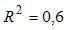 . Следовательно, доля объясненной дисперсии в общей дисперсии зависимой переменной для данного уравнения составляет …
. Следовательно, доля объясненной дисперсии в общей дисперсии зависимой переменной для данного уравнения составляет …

|
|
| 0,6
|
|
|
|
| 0,6%
|
|
|
|
| 0,4
|
|
|
|
| 0,4%
|
Решение:
Уравнение регрессии строится для моделирования зависимой переменной. При этом общая дисперсия зависимой переменной принимается как целое, то есть за 1. Она (1 – общая дисперсия) раскладывается на две части: объясненная уравнением часть и не объясненная уравнением (остаточная) часть. Для каждой части рассчитывается ее доля в общей дисперсии, то есть в 1. Доля объясненной дисперсии в общей есть не что иное как индекс детерминации (для нелинейных уравнений) или коэффициент детерминации (для линейных уравнений), обозначается R2. Доля остаточной дисперсии в общей рассчитывается как разность (1– R2). Доля каждой из частей всегда не больше 1; доля есть часть, поэтому не имеет единицы измерения. Можно рассчитать также процент, тогда долю нужно умножить на 100%, это значение будет показывать, сколько процентов занимает та или иная часть дисперсии (объясненная или остаточная) в общей дисперсии, то есть в 100%. В нашем случае 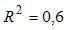 , следовательно, доля объясненной дисперсии зависимой переменной в ее общей дисперсии составляет 0,6 (это правильный вариант ответа); доля остаточной дисперсии зависимой переменной в общей составляет 0,4. В процентном соотношении получаем: доля объясненной дисперсии зависимой переменной в ее общей дисперсии составляет 60%; доля остаточной дисперсии зависимой переменной в общей составляет 40%.
, следовательно, доля объясненной дисперсии зависимой переменной в ее общей дисперсии составляет 0,6 (это правильный вариант ответа); доля остаточной дисперсии зависимой переменной в общей составляет 0,4. В процентном соотношении получаем: доля объясненной дисперсии зависимой переменной в ее общей дисперсии составляет 60%; доля остаточной дисперсии зависимой переменной в общей составляет 40%.
Поэтому правильный вариант ответа «0,6».
 ЗАДАНИЕ N 17 сообщить об ошибке
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Методы оценки параметров систем одновременных уравнений: косвенный метод наименьших квадратов (КМНК) и двухшаговый метод наименьших квадратов (ДМНК)
При проверке счетного правила выяснилось, что для всех уравнений системы одновременных уравнений выполняется необходимое условие идентификации и все уравнения по счетному правилу точно идентифицируемы. Чтобы получить структурные коэффициенты системы, действия нужно выполнить в следующем порядке:
|
|
|
| для каждого уравнения проверить условие неравенства нулю определителя матрицы коэффициентов, присутствующих в других уравнениях, но отсутствующих в данном уравнении
|
|
|
|
| преобразовать структурную форму модели в приведенную форму модели
|
|
|
|
| для каждого уравнения приведенной формы модели обычным методом наименьших квадратов оценить приведенные коэффициенты
|
|
|
|
| коэффициенты приведенной формы модели преобразовать в параметры структурной модели
|
Решение:
Так как выполнение счетного правила является только необходимым, но не достаточным условием идентификации, то сначала нужно проверить выполнение достаточного условия идентификации.
Другими словами, сначала для каждого уравнения нужно проверить условие неравенства нулю определителя матрицы коэффициентов, присутствующих в других уравнениях, но отсутствующих в данном уравнении.
После проверки выполнения достаточного условия идентификации можно применять косвенный метод наименьших квадратов. Применяем косвенный метод наименьших квадратов, поскольку все уравнения системы являются точно идентифицируемыми. Второе действие – преобразование структурной формы модели в приведенную форму модели.
Третье действие – нахождение для каждого уравнения приведенной формы модели обычным методом наименьших квадратов приведенных коэффициентов.
И, наконец, четвертое действие – преобразование коэффициентов приведенной формы модели в параметры структурной модели.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 260–266.
Кремер, Н.Ш. Эконометрика: учеб. для студентов вузов / Н. Ш. Кремер, Б. А. Путко; ред. Н. Ш. Кремер. - М.: ЮНИТИ, 2002. С.182–200.
Магнус, Ян Р. Эконометрика: нач. курс: [учеб. для студентов вузов по экон. специальностям] / Я. Р. Магнус, П. К. Катышев, А. А. Пересецкий; Акад. нар. хоз-ва при Правительстве РФ. - М.: Дело, 2005. С.197–215.
 ЗАДАНИЕ N 18 сообщить об ошибке
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Классификация систем уравнений
Установите соответствие между видом и классом системы эконометрических уравнений:
(1) 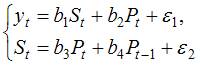
(2) 
|
|
|
| система одновременных уравнений с лаговыми переменными
|
|
|
|
| система независимых уравнений
|
|
|
|
| система одновременных уравнений без лаговых переменных
|
Решение:
Рассмотрим каждую из систем эконометрических уравнений.
В системе (1) в правой части первого уравнения стоит переменная St, которая во втором уравнении находится в левой части, следовательно, система является системой одновременных уравнений. Во втором уравнении системы (1) одновременно с переменной Pt находится лаговая переменная Pt-1, поэтому система (1) является системой одновременных уравнений с лаговыми переменными.
В системе (2) в левой части представлены переменные yt и wt, которые не входят в правую часть уравнений системы, поэтому система (2) является системой независимых уравнений.
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С. 341–345.
Эконометрика: учеб. / под ред. И.И. Елисеевой. – М.: Проспект, 2009. – С. 230–233.
 ЗАДАНИЕ N 19 сообщить об ошибке
ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Идентификация систем эконометрических уравнений
Даны структурная и приведенная формы модели системы одновременных уравнений:  и
и 
Установите соответствие между наименованием обозначения и его видом:
(1) приведенный коэффициент
(2) структурный коэффициент
(3) переменная модели
Решение:
Рассмотрим каждое из наименований обозначений.
(1) – приведенный коэффициент (коэффициент приведенной формы модели), являющийся нелинейной комбинацией структурных коэффициентов (коэффициентов структурной формы модели), из предложенных вариантов ему соответствует обозначение  .
.
(2) – структурный коэффициент  , или коэффициент структурной формы модели, которая отражает структуру связей между переменными.
, или коэффициент структурной формы модели, которая отражает структуру связей между переменными.
(3) – переменная модели, может быть зависимой или независимой, из предложенных вариантов данному понятию соответствует обозначение 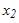 .
.
Вариант ответа « » не соответствует ни одному из наименований, так как это ошибка уравнения системы, неправильный вариант ответа.
» не соответствует ни одному из наименований, так как это ошибка уравнения системы, неправильный вариант ответа.
 ЗАДАНИЕ N 20 сообщить об ошибке
ЗАДАНИЕ N 20 сообщить об ошибке
Тема: Общие понятия о системах уравнений, используемых в эконометрике
Система эконометрических уравнений не может состоять из …

|
|
| одного уравнения регрессии
|

|
|
| совокупности неравенств
|
|
|
|
| трех уравнений регрессии
|
|
|
|
| пяти уравнений регрессии
|
 ЗАДАНИЕ N 21 сообщить об ошибке
ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Модели стационарных и нестационарных временных рядов и их идентификация
Для стационарных временных рядов y1, у2, … yt, …, yn (t = 1, …, n) автокорреляция зависит только от величины …

|
|
| лага
|
|
|
|
| количества уровней ряда
|
|
|
|
| математического ожидания значений уровня ряда
|
|
|
|
| начального значения процесса
|
 ЗАДАНИЕ N 22 сообщить об ошибке
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Структура временного ряда
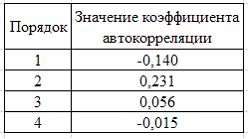
Данная таблица значений автокорреляционной функции соответствует структуре временного ряда …
 ЗАДАНИЕ N 23 сообщить об ошибке
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Аддитивная и мультипликативная модели временных рядов
Уровень временного ряда (yt) формируется под воздействием различных факторов – компонент: Т (тенденция), S (циклические и/или сезонные колебания), Е (случайные факторы). Мультипликативную модель временного ряда не формируют следующие значения компонент уровня временного ряда …

|
|
| yt = 7; T = -3,5; S = -2; E = -1
|
|
|
|
| yt = 7; T = 7; S = 1; E = 1
|
|
|
|
| yt = 7; T = 3,5; S = 2; E = 1
|
|
|
|
| yt = 7; T = 3,5; S = -2; E = -1
|
 ЗАДАНИЕ N 24 сообщить об ошибке
ЗАДАНИЕ N 24 сообщить об ошибке
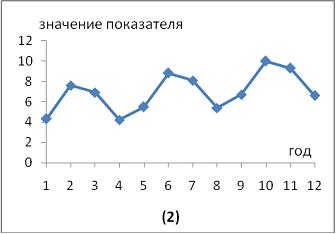
Тема: Временные ряды данных: характеристики и общие понятия
Изображенный на рисунке временной ряд содержит следующие компоненты:


|
|
| убывающую тенденцию и случайную компоненту
|
|
|
|
| возрастающую тенденцию и случайную компоненту
|
|
|
|
| убывающую сезонную компоненту и случайную компоненту
|
|
|
|
| сезонную компоненту и убывающую случайную компоненту
|



 ЗАДАНИЕ N 2 сообщить об ошибке
ЗАДАНИЕ N 2 сообщить об ошибке определяются из условия ______ остатков
определяются из условия ______ остатков  .
. ,
,  . По данным характеристикам можно сделать вывод о том, что …
. По данным характеристикам можно сделать вывод о том, что … . Рассчитаем статистику Дарбина – Уотсона по формуле
. Рассчитаем статистику Дарбина – Уотсона по формуле  . Нам известны критические значения статистики Дарбина – Уотсона для заданного количества параметров при неизвестном и количестве наблюдений
. Нам известны критические значения статистики Дарбина – Уотсона для заданного количества параметров при неизвестном и количестве наблюдений  минимальна. Отклонение
минимальна. Отклонение  , посчитанное для i -го наблюдения, является ошибкой модели. При применении МНК относительно остатков регрессионной модели выдвигаются определенные предпосылки: случайный характер остатков, нулевая средняя величина, отсутствие автокорреляции в остатках, постоянная дисперсия (гомоскедастичность) остатков, подчинение нормальному закону распределения. Если остатки не удовлетворяют предпосылкам МНК, то применение обычного (традиционного) МНК нецелесообразно. Если остатки автокоррелированны и/или гетероскедастичны, то проводят преобразование переменных и расчет оценок параметров осуществляют с использованием обобщенного метода наименьших квадратов (ОМНК). Верным вариантом является «обобщенный».
, посчитанное для i -го наблюдения, является ошибкой модели. При применении МНК относительно остатков регрессионной модели выдвигаются определенные предпосылки: случайный характер остатков, нулевая средняя величина, отсутствие автокорреляции в остатках, постоянная дисперсия (гомоскедастичность) остатков, подчинение нормальному закону распределения. Если остатки не удовлетворяют предпосылкам МНК, то применение обычного (традиционного) МНК нецелесообразно. Если остатки автокоррелированны и/или гетероскедастичны, то проводят преобразование переменных и расчет оценок параметров осуществляют с использованием обобщенного метода наименьших квадратов (ОМНК). Верным вариантом является «обобщенный». парной линейной регрессии
парной линейной регрессии  нельзя рассчитать по формуле …
нельзя рассчитать по формуле …


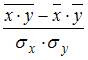
 , и остаточная сумма квадратов отклонений
, и остаточная сумма квадратов отклонений  , то сумма квадратов отклонений, объясненная регрессией, равна …
, то сумма квадратов отклонений, объясненная регрессией, равна … , где y – зависимая переменная, xj – независимая переменная (j = 1,…, k; k – количество независимых переменных), f – тип функциональной зависимости (математическая функция),
, где y – зависимая переменная, xj – независимая переменная (j = 1,…, k; k – количество независимых переменных), f – тип функциональной зависимости (математическая функция),  – случайные факторы. Спецификация эконометрической модели уравнения регрессии определяется видом функции f, а также числом независимых переменных (факторов или регрессоров). Парная и множественная регрессия характеризуют количество независимых переменных хj в уравнении регрессии (парная – одна независимая переменная; множественная – не меньше двух независимых переменных). Поэтому верным вариантом является «простую и множественную» регрессии. Вариант ответа «линейную и нелинейную» – неверный, так как это характеризует вид зависимости (математической функции) f. Варианты «множественную и многофакторную» и «простую и парную» отражают один из классификационных признаков и не описывают всей совокупности эконометрических моделей регрессии.
– случайные факторы. Спецификация эконометрической модели уравнения регрессии определяется видом функции f, а также числом независимых переменных (факторов или регрессоров). Парная и множественная регрессия характеризуют количество независимых переменных хj в уравнении регрессии (парная – одна независимая переменная; множественная – не меньше двух независимых переменных). Поэтому верным вариантом является «простую и множественную» регрессии. Вариант ответа «линейную и нелинейную» – неверный, так как это характеризует вид зависимости (математической функции) f. Варианты «множественную и многофакторную» и «простую и парную» отражают один из классификационных признаков и не описывают всей совокупности эконометрических моделей регрессии. величина параметра а характеризует среднее по совокупности значение зависимой переменной, при значениях ___, равных 0.
величина параметра а характеризует среднее по совокупности значение зависимой переменной, при значениях ___, равных 0. – номер независимой переменной в модели, k – общее количество независимых переменных в модели); a, bj – параметры уравнения;
– номер независимой переменной в модели, k – общее количество независимых переменных в модели); a, bj – параметры уравнения; 

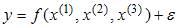


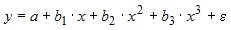

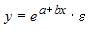

 является нелинейным по переменной х, но линейным по параметрам. Уравнения
является нелинейным по переменной х, но линейным по параметрам. Уравнения  и
и  также являются нелинейными по переменной х, но линейными по параметрам. Поэтому правильный вариант ответа – «
также являются нелинейными по переменной х, но линейными по параметрам. Поэтому правильный вариант ответа – «



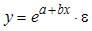
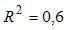 . Следовательно, доля объясненной дисперсии в общей дисперсии зависимой переменной для данного уравнения составляет …
. Следовательно, доля объясненной дисперсии в общей дисперсии зависимой переменной для данного уравнения составляет …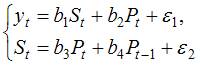

 и
и