При методе наименьших квадратов параметры уравнения парной линейной регрессии  определяются из условия ______ остатков
определяются из условия ______ остатков  .
.

|
|
| минимизации суммы квадратов
|
|
|
|
| равенства нулю суммы квадратов
|
|
|
|
| минимизации модулей
|
|
|
|
| равенства нулю
|
Решение:
При методе наименьших квадратов параметры уравнения парной линейной регрессии  определяются из условия минимизации суммы квадратов остатков
определяются из условия минимизации суммы квадратов остатков  .
.
Эконометрика. Краткий курс: учеб. пособие / С.А. Айвазян, С.С. Иванова. – М.: Маркет ДС, 2007. – С.59–61.
 ЗАДАНИЕ N 2 сообщить об ошибке
ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Обобщенный метод наименьших квадратов (ОМНК)
Для оценки параметров регрессионной модели с коррелированными остатками используется _______ метод наименьших квадратов.

|
|
| обобщенный
|
|
|
|
| традиционный
|
|
|
|
| двухшаговый
|
|
|
|
| косвенный
|
Решение:
Метод наименьших квадратов (МНК) позволяет рассчитать такие оценки параметров линейной модели регрессии, для которых сумма квадратов отклонений фактических значений зависимой переменной y от ее модельных (теоретических) значений  минимальна. Отклонение
минимальна. Отклонение  , посчитанное для i -го наблюдения, является ошибкой модели. При применении МНК относительно остатков регрессионной модели выдвигаются определенные предпосылки: случайный характер остатков, нулевая средняя величина, отсутствие автокорреляции в остатках, постоянная дисперсия (гомоскедастичность) остатков, подчинение нормальному закону распределения. Если остатки не удовлетворяют предпосылкам МНК, то применение обычного (традиционного) МНК нецелесообразно. Если остатки автокоррелированны и/или гетероскедастичны, то проводят преобразование переменных и расчет оценок параметров осуществляют с использованием обобщенного метода наименьших квадратов (ОМНК). Верным вариантом является «обобщенный».
, посчитанное для i -го наблюдения, является ошибкой модели. При применении МНК относительно остатков регрессионной модели выдвигаются определенные предпосылки: случайный характер остатков, нулевая средняя величина, отсутствие автокорреляции в остатках, постоянная дисперсия (гомоскедастичность) остатков, подчинение нормальному закону распределения. Если остатки не удовлетворяют предпосылкам МНК, то применение обычного (традиционного) МНК нецелесообразно. Если остатки автокоррелированны и/или гетероскедастичны, то проводят преобразование переменных и расчет оценок параметров осуществляют с использованием обобщенного метода наименьших квадратов (ОМНК). Верным вариантом является «обобщенный».
 ЗАДАНИЕ N 3 сообщить об ошибке
ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Свойства оценок параметров эконометрической модели, получаемых при помощи МНК
Если оценка параметра является смещенной, то нарушается предпосылка метода наибольших квадратов о _____ остатков.

|
|
| нулевой средней величине
|
|
|
|
| нормальном законе распределения
|
|
|
|
| случайном характере
|
|
|
|
| гомоскедастичности
|
 ЗАДАНИЕ N 4 сообщить об ошибке
ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Предпосылки МНК, методы их проверки
Из перечисленного условием выполнения предпосылок метода наименьших квадратов не является ____ остатков.

|
|
| гетероскедатичность
|
|
|
|
| случайный характер
|
|
|
|
| нулевая средняя величина
|
|
|
|
| отсутствие автокорреляции
|
Решение:
Условия, необходимые для несмещенных, состоятельных и эффективных оценок, представляют собой предпосылки МНК.
Исследования остатков предполагают проверку наличия следующих пяти предпосылок МНК:
– случайный характер остатков;
– нулевая средняя величина остатков, не зависящая от  ;
;
– гомоскедастичность остатков;
– отсутствие автокорреляции остатков;
– подчинение остатков нормальному закону распределения.
Гетероскедатичность остатков не является предпосылкой МНК.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С.184–186.
Бывшев В.А. Эконометрика: учеб. пособие / В.А. Бывшев. – М.: Финансы и статистика, 2008. – С.268–301.
 ЗАДАНИЕ N 5 сообщить об ошибке
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Виды нелинейных уравнений регрессии
Среди предложенных нелинейных зависимостей внутренне линейной является …
Решение:
Среди предложенных нелинейных зависимостей зависимость  является внутренне линейной, хотя она и нелинейна по переменным, поскольку с помощью логарифмирования ее можно привести к линейному виду. Остальные функции внутренне нелинейны: они не могут быть приведены к линейному виду.
является внутренне линейной, хотя она и нелинейна по переменным, поскольку с помощью логарифмирования ее можно привести к линейному виду. Остальные функции внутренне нелинейны: они не могут быть приведены к линейному виду.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 86–90.
Бывшев В.А. Эконометрика: учеб. пособие / В.А. Бывшев. – М.: Финансы и статистика, 2008. – С.331–346.
 ЗАДАНИЕ N 6 сообщить об ошибке
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Оценка качества нелинейных уравнений регрессии
Для нелинейной регрессионной модели зависимости рассчитано значение индекса детерминации R2 = 0,9. Тогда значение индекса корреляции составит …
 ЗАДАНИЕ N 7 сообщить об ошибке
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Нелинейные зависимости в экономике
Нелинейным уравнением парной регрессии является …
Решение:
Рассмотрим каждую из моделей:  – линейное уравнение множественной регрессии;
– линейное уравнение множественной регрессии;  – нелинейное уравнение множественной регрессии;
– нелинейное уравнение множественной регрессии;  – линейное уравнение парной регрессии, которое можно переписать в виде
– линейное уравнение парной регрессии, которое можно переписать в виде  ;
;  – нелинейное уравнение парной регрессии – модель, которая является правильным вариантом ответа. Остальные модели не подходят под спецификацию уравнения регрессии, заданную в постановке вопроса, поэтому не являются правильными вариантами ответов.
– нелинейное уравнение парной регрессии – модель, которая является правильным вариантом ответа. Остальные модели не подходят под спецификацию уравнения регрессии, заданную в постановке вопроса, поэтому не являются правильными вариантами ответов.
 ЗАДАНИЕ N 8 сообщить об ошибке
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Линеаризация нелинейных моделей регрессии
Для линеаризации нелинейной функции  может быть применен метод ______ и замены переменных.
может быть применен метод ______ и замены переменных.

|
|
| обращения
|
|
|
|
| потенцирования
|
|
|
|
| логарифмирования
|
|
|
|
| разложения функции в ряд Тейлора
|
Решение:
Обратив обе части равенства, получим линейную форму для переменной  :
:  . Коэффициенты данной модели могут быть найдены стандартным методом наименьших квадратов.
. Коэффициенты данной модели могут быть найдены стандартным методом наименьших квадратов.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 96–99.
Бывшев В.А. Эконометрика: учеб. пособие / В.А. Бывшев. – М.: Финансы и статистика, 2008. – С.331–346.
 ЗАДАНИЕ N 9 сообщить об ошибке
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Оценка значимости параметров эконометрической модели
Если параметр эконометрической модели является статистически значимым, то его значение признается …

|
|
| отличным от 0
|
|
|
|
| равным 0
|
|
|
|
| равным 1
|
|
|
|
| равным коэффициенту парной корреляции
|
Решение:
Эконометрическая модель дает количественное выражение исследуемой зависимости между социально-экономическими показателями. При этом оценка параметров модели осуществляется по некоторой статистической выборке, отражающей данную зависимость для генеральной совокупности однородных объектов. При проверке статистической значимости параметра проверяется статистическая гипотеза о том, что значение параметра модели равно 0 и соответствующая независимая переменная не оказывает влияния на моделируемый показатель (зависимую переменную). Если анализ показал, что параметр значим, то гипотеза о равенстве 0 его значения отвергается, таким образом, значение параметра признается отличным от 0, и влияние соответствующей независимой переменной на моделируемый показатель (зависимую переменную) признается значимым. Правильный вариант ответа – «отличным от 0». Или полный ответ: «Если параметр эконометрической модели является статистически значимым, то его значение признается отличным от 0».
 ЗАДАНИЕ N 10 сообщить об ошибке
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Проверка статистической значимости эконометрической модели
По результатам 50 статистических наблюдений построено уравнение множественной регрессии  Число степеней свободы остаточной суммы квадратов отклонений для этого уравнения равно …
Число степеней свободы остаточной суммы квадратов отклонений для этого уравнения равно …
 ЗАДАНИЕ N 11 сообщить об ошибке
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Оценка качества подбора уравнения
Для регрессионной модели вида  , где
, где 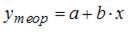 рассчитаны дисперсии:
рассчитаны дисперсии:  ;
;  ;
; 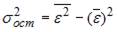 . Тогда величина
. Тогда величина 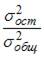 характеризует долю …
характеризует долю …

|
|
| остаточной дисперсии
|
|
|
|
| коэффициента детерминации
|
|
|
|
| коэффициента корреляции
|
|
|
|
| объясненной дисперсии
|
Решение:
Значение коэффициента детерминации  характеризует долю дисперсии зависимой переменной, объясненную построенным уравнением регрессии, в общей дисперсии зависимой переменной. Разность
характеризует долю дисперсии зависимой переменной, объясненную построенным уравнением регрессии, в общей дисперсии зависимой переменной. Разность  характеризует долю остаточной дисперсии, которая может быть рассчитана также по формуле
характеризует долю остаточной дисперсии, которая может быть рассчитана также по формуле 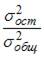 . Поэтому отношение
. Поэтому отношение 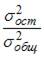 характеризует долю остаточной дисперсии.
характеризует долю остаточной дисперсии.
 ЗАДАНИЕ N 12 сообщить об ошибке
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Оценка тесноты связи
Для регрессионной модели вида  построена на координатной плоскости совокупность точек с координатами
построена на координатной плоскости совокупность точек с координатами  , данное графическое отображение зависимости называется …
, данное графическое отображение зависимости называется …

|
|
| полем корреляции
|
|
|
|
| параметрами уравнения
|
|
|
|
| случайными факторами
|
|
|
|
| множественной регрессией
|
 ЗАДАНИЕ N 13 сообщить об ошибке
ЗАДАНИЕ N 13 сообщить об ошибке
Тема: Линейное уравнение множественной регрессии
Известно, что доля остаточной дисперсии зависимой переменной в ее общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …
Решение:
Коэффициент детерминации 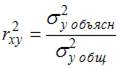 равен доле дисперсии, объясненной регрессией, в общей дисперсии. Величина (
равен доле дисперсии, объясненной регрессией, в общей дисперсии. Величина ( ) показывает долю остаточной дисперсии в общей или дисперсию, вызванную влиянием остальных, не учтенных в модели факторов.
) показывает долю остаточной дисперсии в общей или дисперсию, вызванную влиянием остальных, не учтенных в модели факторов.
 . Значит,
. Значит, 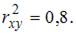
Магнус, Ян Р. Эконометрика: нач. курс: [учеб. для студентов вузов по экон. специальностям] / Я. Р. Магнус, П. К. Катышев, А. А. Пересецкий; Акад. нар. хоз-ва при Правительстве РФ. – М.: Дело, 2005. С.46–50.
 ЗАДАНИЕ N 14 сообщить об ошибке
ЗАДАНИЕ N 14 сообщить об ошибке
Тема: Фиктивные переменные
При исследовании зависимости потребления мяса от уровня дохода и пола потребителя можно рекомендовать …

|
|
| использовать фиктивную переменную – пол потребителя
|

|
|
| разделить совокупность на две: для потребителей женского пола и для потребителей мужского пола
|
|
|
|
| использовать фиктивную переменную – уровень дохода
|
|
|
|
| исключить из рассмотрения пол потребителя, так как данный фактор нельзя измерить количественным образом
|
Решение:
При построении регрессионной модели может возникнуть ситуация, когда необходимо включить в уравнение помимо количественных переменных переменные, отражающие некоторые атрибутивные признаки (пол, образование, регион и т.п.). Такого рода качественные переменные называются «фиктивными» (dummy) переменными. Они отражают неоднородность исследуемой статистической совокупности и используются для более качественного моделирования зависимостей в таких неоднородных объектах наблюдения. При моделировании отдельных зависимостей по неоднородным данным можно также воспользоваться способом разделения всей совокупности неоднородных данных на несколько отдельных совокупностей, количество которых равно количеству состояний dummy-переменной. Таким образом правильными вариантами ответов являются: «использовать фиктивную переменную – пол потребителя» и «разделить совокупность на две: для потребителей женского пола и для потребителей мужского пола».
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С. 121–127.
 ЗАДАНИЕ N 15 сообщить об ошибке
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Спецификация эконометрической модели
Особенность эконометрики как прикладной науки заключается в ____ существующих взаимосвязей социально-экономических показателей и систем.

|
|
| количественном измерении
|
|
|
|
| качественном описании
|
|
|
|
| формулировании теорий
|
|
|
|
| схематическом описании
|
 ЗАДАНИЕ N 16 сообщить об ошибке
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Отбор факторов, включаемых в модель множественной регрессии
Для эконометрической модели линейного уравнения множественной регрессии вида  построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х(1), х(2), х(3) – независимые переменные):
построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х(1), х(2), х(3) – независимые переменные):

Количество пар коллинеарных независимых переменных в данной модели равно …

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
При построении модели множественной регрессии необходимо исключить возможность существования тесной линейной зависимости между объясняющими переменными, что ведет к проблеме мультиколлинеарности. При этом осуществляют проверку коэффициентов линейной корреляции для каждой пары объясняющих переменных. Эти значения отражены в матрице парных коэффициентов линейной корреляции. Считается, что наличие значений коэффициентов парной корреляции между объясняющими переменными, превышающих по абсолютной величине 0,7, отражает тесную связь между этими переменными. Такие объясняющие переменные называются коллинеарными. В матрице значения двух парных коэффициентов линейной корреляции по абсолютной величине превышают 0,7 ( ;
;  ). Верным вариантом ответа является «2». Другие варианты ответов являются неверными. Теснота связи с переменной y в данном случае не рассматривается, так как переменная y не является объясняющей переменной. Поэтому другие значения в матрице, превышающие 0,7, не отражают пары коллинеарных объясняющих переменных.
). Верным вариантом ответа является «2». Другие варианты ответов являются неверными. Теснота связи с переменной y в данном случае не рассматривается, так как переменная y не является объясняющей переменной. Поэтому другие значения в матрице, превышающие 0,7, не отражают пары коллинеарных объясняющих переменных.
 ЗАДАНИЕ N 17 сообщить об ошибке
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Модели стационарных и нестационарных временных рядов и их идентификация
Для стационарных временных рядов y1, у2, … yt, …, yn (t = 1, …, n) автоковариация зависит только от величины …

|
|
| лага
|
|
|
|
| количества уровней ряда
|
|
|
|
| математического ожидания значений уровня ряда.
|
|
|
|
| начального значения процесса
|
Решение:
Стохастический процесс (процесс, развивающийся в соответствии с законами теории вероятности) является стационарным, если выполняется ряд условий: неизменные постоянные величины среднего значения и дисперсии временного ряда; постоянные автокорреляция и автоковариация временного ряда, зависящие только от величины лага. Поэтому правильный вариант ответа – зависит только от величины «лага».
 ЗАДАНИЕ N 18 сообщить об ошибке
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Временные ряды данных: характеристики и общие понятия
Выраженную положительную тенденцию содержит ряд …
Решение:
Ряд имеет выраженную положительную тенденцию, если уровни ряда увеличиваются с увеличением периода времени t.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 297.
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С.284–290.
 ЗАДАНИЕ N 19 сообщить об ошибке
ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Структура временного ряда
Значение коэффициента автокорреляции второго порядка равно (-0,6), следовательно, ряд содержит …

|
|
| тенденцию
|
|
|
|
| убывающую тенденцию
|
|
|
|
| затухающую сезонную волну периодичностью 2 момента времени
|
|
|
|
| полиномиальную тенденцию с точкой минимума
|
Решение:
Структура временного ряда определяется по значениям коэффициента автокорреляции, рассчитанным для разных порядков. Коэффициент автокорреляции характеризует тесноту связи между уровнями исходного ряда и уровнями этого же ряда, сдвинутыми на значение порядка коэффициента автокорреляции. Если временной ряд содержит тенденцию, то наиболее высокое (максимальное или чуть меньше, чем максимальное) значение наблюдается у коэффициента автокорреляции первого и/или второго порядка. Однако, по знаку коэффициента автокорреляции нельзя делать вывод о направленности тенденции. Поэтому вариант «ряд содержит убывающую тенденцию» является ошибочным, так как ряд при данном значении коэффициента автокорреляции может содержать и положительную тенденцию. Правильный вариант – «ряд содержит тенденцию».
Эконометрика: учеб. / под ред. И.И. Елисеевой. – М.: Проспект, 2009. – С. 132–138.
 ЗАДАНИЕ N 20 сообщить об ошибке
ЗАДАНИЕ N 20 сообщить об ошибке
Тема: Аддитивная и мультипликативная модели временных рядов
Для аддитивной модели временного ряда Y = T + S + E лаг модели равен 4 и известны значения трех скорректированных сезонных компонент:  ,
,  ,
,  .
. 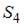 равна …
равна …
 ЗАДАНИЕ N 21 сообщить об ошибке
ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Общие понятия о системах уравнений, используемых в эконометрике
Для системы одновременных уравнений
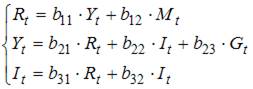 , где
, где
 – процентная ставка,
– процентная ставка,
 – реальный ВВП,
– реальный ВВП,
 – объем денежной массы,
– объем денежной массы,
 – внутренние инвестиции,
– внутренние инвестиции,
 – реальные государственные расходы,
– реальные государственные расходы,
эндогенными являются переменные …
Решение:
Эндогенными называются зависимые переменные, которые стоят в левых частях уравнений, число эндогенных переменных равно числу уравнений системы. В данном случае эндогенными являются  ,
,  и
и  .
.
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С.341–355.
 ЗАДАНИЕ N 22 сообщить об ошибке
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Методы оценки параметров систем одновременных уравнений: косвенный метод наименьших квадратов (КМНК) и двухшаговый метод наименьших квадратов (ДМНК)
Дана система одновременных эконометрических уравнений:

Система является точно идентифицируемой. Определите последовательность этапов алгоритма оценки ее параметров.
|
|
|
| преобразование структурной формы модели в приведенную форму вида 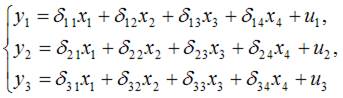
|
|
|
|
| оценивание параметров приведенной формы модели (приведенных коэффициентов)  для каждого уравнения приведенной формы модели обычным МНК оцениваются для каждого уравнения приведенной формы модели обычным МНК оцениваются
|
|
|
|
| трансформация коэффициентов приведенной формы модели в параметры структурной формы модели  и и 
|
|
|
|
| подстановка найденных значений коэффициентов в структурную форму системы эконометрических уравнений
|
Решение:
В случае точно идентифицируемой структурной формы модели для оценки ее параметров применяют косвенный метод наименьших квадратов (КМНК). При этом соблюдают следующую последовательность этапов КМНК:
1) структурная форма модели преобразовывается в приведенную форму модели; так как в системе 4 экзогенных переменных – (х1, х2, х3 и х4),то у правой части приведенной формы модели записывается сумма четырех произведений соответствующих коэффициентов приведенной формы и экзогенных переменных; для данной системы приведенная форма будет иметь вид

2) для каждого уравнения приведенной формы модели обычным МНК оцениваются параметры приведенной формы модели – приведенные коэффициенты  ;
;
3) коэффициенты приведенной формы модели трансформируются в параметры структурной формы модели  и
и  ;
;
4) найденные значения коэффициентов подставляются в структурную форму системы эконометрических уравнений.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 265–266.
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С. 347–353.
 ЗАДАНИЕ N 23 сообщить об ошибке
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Классификация систем уравнений
Установите соответствие между видом и классом системы эконометрических уравнений:
(1) 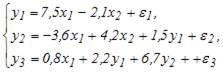
(2) 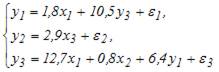
|
|
|
| система рекурсивных уравнений
|
|
|
|
| система взаимозависимых (одновременных) уравнений
|
|
|
|
| система независимых уравнений
|
Решение:
Рассмотрим каждую из систем эконометрических уравнений.
В системе (1) в правой части уравнений стоят как зависимые переменные y других уравнений, так и независимые переменные х, при этом каждое последующее уравнение в правой части включает зависимые переменные у только предыдущих уравнений системы. Поэтому система (1) является системой рекурсивных уравнений.
В системе (2) в правой части уравнений стоят как зависимые переменные y других уравнений, так и независимые переменные х. Порядок следования зависимых переменных у в правой части уравнений не зависит от количества предыдущих уравнений. Поэтому система (2) является системой взаимозависимых (одновременных) уравнений.
Вариант ответа «система независимых уравнений» не подходит ни к одной из предложенных систем, т.к. в такой системе в правой части уравнений должны стоять только независимые переменные х, это неправильный вариант ответа.
 ЗАДАНИЕ N 24 сообщить об ошибке
ЗАДАНИЕ N 24 сообщить об ошибке
Тема: Идентификация систем эконометрических уравнений
Дана структурная форма модели системы одновременных уравнений: 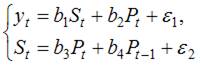
Установите соответствие между обозначением и его наименованием:
(1) 
(2) 
(3) 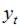
|
|
|
| ошибка модели
|
|
|
|
| лаговая переменная
|
|
|
|
| эндогенная переменная
|
|
|
|
| структурный коэффициент
|
Решение:
Рассмотрим каждое из обозначений.
(1)  – ошибка модели, учитывает влияние факторов случайного характера на зависимую переменную первого уравнения.
– ошибка модели, учитывает влияние факторов случайного характера на зависимую переменную первого уравнения.
(2)  – лаговая переменная, характеризующая значение переменной
– лаговая переменная, характеризующая значение переменной  в предыдущий период.
в предыдущий период.
(3) 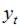 – зависимая переменная, то есть эндогенная переменная, входящая в левую часть первого уравнения системы.
– зависимая переменная, то есть эндогенная переменная, входящая в левую часть первого уравнения системы.
Вариант ответа «структурный коэффициент» не является наименованием ни одного из обозначений; структурными коэффициентами в данной системе являются коэффициенты  .
.

 определяются из условия ______ остатков
определяются из условия ______ остатков  .
.
 ЗАДАНИЕ N 2 сообщить об ошибке
ЗАДАНИЕ N 2 сообщить об ошибке минимальна. Отклонение
минимальна. Отклонение  , посчитанное для i -го наблюдения, является ошибкой модели. При применении МНК относительно остатков регрессионной модели выдвигаются определенные предпосылки: случайный характер остатков, нулевая средняя величина, отсутствие автокорреляции в остатках, постоянная дисперсия (гомоскедастичность) остатков, подчинение нормальному закону распределения. Если остатки не удовлетворяют предпосылкам МНК, то применение обычного (традиционного) МНК нецелесообразно. Если остатки автокоррелированны и/или гетероскедастичны, то проводят преобразование переменных и расчет оценок параметров осуществляют с использованием обобщенного метода наименьших квадратов (ОМНК). Верным вариантом является «обобщенный».
, посчитанное для i -го наблюдения, является ошибкой модели. При применении МНК относительно остатков регрессионной модели выдвигаются определенные предпосылки: случайный характер остатков, нулевая средняя величина, отсутствие автокорреляции в остатках, постоянная дисперсия (гомоскедастичность) остатков, подчинение нормальному закону распределения. Если остатки не удовлетворяют предпосылкам МНК, то применение обычного (традиционного) МНК нецелесообразно. Если остатки автокоррелированны и/или гетероскедастичны, то проводят преобразование переменных и расчет оценок параметров осуществляют с использованием обобщенного метода наименьших квадратов (ОМНК). Верным вариантом является «обобщенный». ;
;





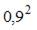
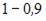




 ;
;  может быть применен метод ______ и замены переменных.
может быть применен метод ______ и замены переменных. :
:  . Коэффициенты данной модели могут быть найдены стандартным методом наименьших квадратов.
. Коэффициенты данной модели могут быть найдены стандартным методом наименьших квадратов. Число степеней свободы остаточной суммы квадратов отклонений для этого уравнения равно …
Число степеней свободы остаточной суммы квадратов отклонений для этого уравнения равно … , где
, где 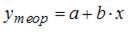 рассчитаны дисперсии:
рассчитаны дисперсии:  ;
;  ;
; 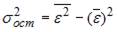 . Тогда величина
. Тогда величина 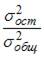 характеризует долю …
характеризует долю … характеризует долю дисперсии зависимой переменной, объясненную построенным уравнением регрессии, в общей дисперсии зависимой переменной. Разность
характеризует долю дисперсии зависимой переменной, объясненную построенным уравнением регрессии, в общей дисперсии зависимой переменной. Разность  характеризует долю остаточной дисперсии, которая может быть рассчитана также по формуле
характеризует долю остаточной дисперсии, которая может быть рассчитана также по формуле  построена на координатной плоскости совокупность точек с координатами
построена на координатной плоскости совокупность точек с координатами  , данное графическое отображение зависимости называется …
, данное графическое отображение зависимости называется …

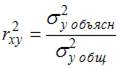 равен доле дисперсии, объясненной регрессией, в общей дисперсии. Величина (
равен доле дисперсии, объясненной регрессией, в общей дисперсии. Величина ( ) показывает долю остаточной дисперсии в общей или дисперсию, вызванную влиянием остальных, не учтенных в модели факторов.
) показывает долю остаточной дисперсии в общей или дисперсию, вызванную влиянием остальных, не учтенных в модели факторов.  . Значит,
. Значит, 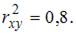
 построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х(1), х(2), х(3) – независимые переменные):
построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х(1), х(2), х(3) – независимые переменные):
 ;
;  ). Верным вариантом ответа является «2». Другие варианты ответов являются неверными. Теснота связи с переменной y в данном случае не рассматривается, так как переменная y не является объясняющей переменной. Поэтому другие значения в матрице, превышающие 0,7, не отражают пары коллинеарных объясняющих переменных.
). Верным вариантом ответа является «2». Другие варианты ответов являются неверными. Теснота связи с переменной y в данном случае не рассматривается, так как переменная y не является объясняющей переменной. Поэтому другие значения в матрице, превышающие 0,7, не отражают пары коллинеарных объясняющих переменных.



 ,
,  ,
,  .
. 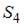 равна …
равна …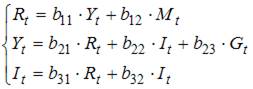 , где
, где – процентная ставка,
– процентная ставка, – реальный ВВП,
– реальный ВВП, – объем денежной массы,
– объем денежной массы, – внутренние инвестиции,
– внутренние инвестиции, – реальные государственные расходы,
– реальные государственные расходы,
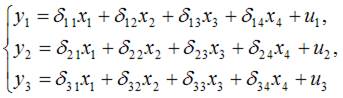
 для каждого уравнения приведенной формы модели обычным МНК оцениваются
для каждого уравнения приведенной формы модели обычным МНК оцениваются
 и
и 

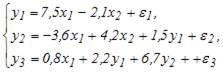
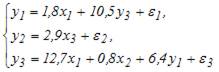
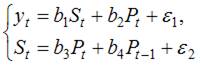


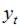
 в предыдущий период.
в предыдущий период. .
.


