
А22 Однородная балка длиной L =6 м лежит серединой на опоре. Слева к балке прикреплен груз на расстоянии b =1 м от конца массой M =30 кг. Какую силу нужно приложить к балке справа, чтобы она находилась в равновесии?
| 1) 200 Н
| 2) 300 Н
| 3) 400 Н
| 4) 600 Н
|
А23 В батарею водяного отопления вода поступает при температуре 70° С по трубе площадью поперечного сечения 500 мм2 со скоростью 1,2 см/с, а выходит из батареи, имея более низкую температуру. На сколько градусов температура на выходе ниже, чем на входе, если отапливаемое помещение в течение суток получает 11 МДж теплоты? Ответ округлить до целых.
| 1) 3° С
| 2) 4° С
| 3) 5° С
| 4) 6° С
|
А24 Чему равна масса шарика зарядом 2 нКл, если он в однородном электрическом поле напряженностью 80 В/см за три минуты прошел путь 81 см? Ответ привести в граммах, округлить до целых.
| 1) 32 г
| 2) 80 г
| 3) 160 г
| 4) 320 г
|
А25 У пружинного маятника циклическая частота была 5 рад/с, а после смены пружины стала 3 рад/с. Жесткость пружины была уменьшена на 144 Н/м. Определите массу груза.
| 1) 7 кг
| 2) 8 кг
| 3) 9 кг
| 4) 10 кг
|
Не забудьте перенести все ответы в бланк ответов № 1
| Полное решение задач С1–С6 необходимо записать в бланке ответов № 2. При оформлении решения в бланке ответов № 2 запишите сначала номер задания (С1, С2 и т.д.), а затем решение соответствующей задачи. Ответы записывайте четко и разборчиво.
|
С1 При движении велосипедиста по закруглению ему приходится наклоняться. Объясните, почему это происходит, и получите соотношение между углом наклона, скоростью движения и радиусом кривизны закругления.
Полное правильное решение каждой из задач С2–С6 должно содержать законы и формулы, применение которых необходимо и достаточно для решения задачи, а также математические преобразования, расчеты с численным ответом и при необходимости рисунок, поясняющий решение.
С2 На гладкой горизонтальной поверхности лежит доска массы M =6 кг, а на ней брусок массы m =1 кг. Доску начинают тянуть с горизонтальной силой F =10 Н. Коэффициент трения между бруском и доской m=0,2. Какой будет скорость у доски, когда брусок соскользнет с нее, если брусок находится на расстоянии l =1 м от края доски? Какую работу совершит при этом сила F?
С3 Теплоизолированный цилиндр разделён подвижным теплопроводящим поршнем на две части. В одной части цилиндра находится гелий, а в другой – аргон. В начальный момент температура гелия равна 900 К, а аргона – 300 К, объёмы, занимаемые газами, одинаковы, а поршень находится в равновесии. Во сколько раз изменится объём, занимаемый гелием, после установления теплового равновесия, если поршень перемещается без трения? Теплоёмкостью цилиндра и поршня пренебречь.
С4 Между обкладками плоского конденсатора помещена параллельно им стеклянная пластинка, толщина которой составляет h=0,50 расстояния между обкладками. Емкость конденсатора в отсутствие пластинки C =10 нФ. Конденсатор подключен к источнику постоянного напряжения U =100 В. Пластинку медленно извлекли из зазора. Диэлектрическая проницаемость стекла равна 5. Найти изменение энергии конденсатора.

С5 Медный провод сечением 2,5 мм2, согнутый в виде трех сторон квадрата, может поворачиваться вокруг горизонтальной оси OO '. Провод находится в однородном вертикально направленном магнитном поле с индукцией 10 мТл. На какой угол отклонится провод, если пропускать по нему ток 16 А?
С6 Уровни энергии электрона в атоме водорода задаются формулой  эВ, где
эВ, где  . При переходе из некоторого состояния
. При переходе из некоторого состояния  на уровень энергии E 2 атом испускает фотон с длиной волны
на уровень энергии E 2 атом испускает фотон с длиной волны  нм. Какой номер имеет состояние n, из которого перешел атом? Какую длину имела бы волна при переходе атома в состояние E 1?
нм. Какой номер имеет состояние n, из которого перешел атом? Какую длину имела бы волна при переходе атома в состояние E 1?
ЗАДАНИЕ N 1 сообщить об ошибке Тема: Нелинейные зависимости в экономике
Если с увеличением масштабов производства удельный расход сырья сокращается, то моделирование целесообразно проводить на основе …

|
|
| равносторонней гиперболы
|
|
|
|
| степенной функции
|
|
|
|
| параболы второй степени
|
|
|
|
| экспоненциальной функции
|
 ЗАДАНИЕ N 2 сообщить об ошибке
ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Виды нелинейных уравнений регрессии
Уравнением нелинейной регрессии, линейной по параметрам является …
Решение:
Рассмотрим каждую из моделей. Уравнение  является нелинейным как по параметрам, так и по переменным. Уравнение
является нелинейным как по параметрам, так и по переменным. Уравнение  является нелинейным по переменной х, но линейным по параметрам. Уравнения
является нелинейным по переменной х, но линейным по параметрам. Уравнения  и
и  также являются нелинейными по переменной х, но линейными по параметрам. Поэтому правильный вариант ответа – «
также являются нелинейными по переменной х, но линейными по параметрам. Поэтому правильный вариант ответа – « ». Другие модели не удовлетворяют поставленному условию.
». Другие модели не удовлетворяют поставленному условию.
 ЗАДАНИЕ N 3 сообщить об ошибке
ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Линеаризация нелинейных моделей регрессии
Для линеаризации нелинейной функции  может быть применен метод …
может быть применен метод …

|
|
| логарифмирования и замены переменных
|
|
|
|
| разложения функции в ряд Тейлора
|
|
|
|
| потенцирования и замены переменных
|
|
|
|
| обращения и замены переменных
|
 ЗАДАНИЕ N 4 сообщить об ошибке
ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Оценка качества нелинейных уравнений регрессии
Для регрессионной модели зависимости потребления материала на единицу продукции от объема выпуска продукции построено нелинейное уравнение (см. рис.).

Значение индекса детерминации для данного уравнения составляет R2 =0,904.
Следовательно, …

|
|
| объемом выпуска продукции объяснено 90,4% дисперсии потребления материалов на единицу продукции
|
|
|
|
| потреблением материалов на единицу продукции объяснено 90,4% дисперсии объема выпуска продукции
|
|
|
|
| объемом выпуска продукции объяснено 9,6% дисперсии потребления материалов на единицу продукции
|
|
|
|
| потреблением материалов на единицу продукции объяснено 9,6% дисперсии объема выпуска продукции
|
Решение:
Значение индекса детерминации R2 характеризует долю дисперсии зависимой переменной, объясненную независимой переменной (построенным нелинейным уравнением регрессии). В данной модели зависимой переменной является потребление материала на единицу продукции, независимой – объем выпуска продукции. Так как значение индекса детерминации R2 = 0,904, то доля дисперсии зависимой переменной, объясненная независимой переменной, составляет 0,904 или 90,4%. Таким образом, объемом выпуска продукции (независимой переменной) объяснено 90,4% дисперсии потребления материалов на единицу продукции (зависимой переменной).
 ЗАДАНИЕ N 5 сообщить об ошибке
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Оценка качества подбора уравнения
Для регрессионной модели парной регрессии рассчитано значение коэффициента детерминации  (см. рис.).
(см. рис.).

На остаточную дисперсию зависимой переменной приходится _____ общей дисперсии зависимой переменной.

|
|
| 16,9 %
|
|
|
|
| 83,1 %
|
|
|
|
| 0,831 %
|
|
|
|
| 0,169 %
|
 ЗАДАНИЕ N 6 сообщить об ошибке
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Оценка тесноты связи
Самым коротким интервалом изменения коэффициента корреляции для уравнения парной линейной регрессии  является …
является …

|
|
| [–1; 0]
|
|
|
|
| [0; 1]
|
|
|
|
| [–1; 1]
|
|
|
|
| [–2; 2]
|
Решение:
Коэффициент корреляции для парной линейной регрессии в общем случае изменяется в пределах [–1, 1]. Однако так как значение коэффициента регрессии отрицательное, то и значение коэффициента корреляции для уравнения тоже будет отрицательным, значит, самым коротким интервалом изменения коэффициента корреляции для уравнения парной линейной регрессии  будет [–1; 0].
будет [–1; 0].
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 59.
 ЗАДАНИЕ N 7 сообщить об ошибке
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Оценка значимости параметров эконометрической модели
Если параметр эконометрической модели является статистически значимым, то отвергается статистическая гипотеза о том, что его значение …

|
|
| равно 0
|
|
|
|
| отлично от 0
|
|
|
|
| равно 1
|
|
|
|
| равно коэффициенту парной корреляции
|
 ЗАДАНИЕ N 8 сообщить об ошибке
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Проверка статистической значимости эконометрической модели
При оценке статистической значимости построенной эконометрической модели выдвигают ______ гипотезы.

|
|
| статистические
|
|
|
|
| математические
|
|
|
|
| информационные
|
|
|
|
| коллективные
|
 ЗАДАНИЕ N 9 сообщить об ошибке
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Общие понятия о системах уравнений, используемых в эконометрике
Модель равенства спроса и предложения, где предложение  и спрос
и спрос 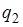 являются линейными функциями цены p, состоит из уравнений …
являются линейными функциями цены p, состоит из уравнений …
 ЗАДАНИЕ N 10 сообщить об ошибке
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Классификация систем уравнений
Установите соответствие между классом и видом системы эконометрических уравнений:
(1) система независимых уравнений
(2) система взаимозависимых (одновременных) уравнений
(3) система рекурсивных уравнений
Решение:
Рассмотрим каждую из систем эконометрических уравнений.
(1) – система независимых уравнений, в такой системе в правой части уравнений стоят только независимые переменные х. Поэтому для системы (1) правильным вариантом ответа является система 
(2) – система взаимозависимых (одновременных) уравнений, в правой части уравнений такой системы стоят как зависимые переменные y других уравнений, так и независимые переменные х. Порядок следования зависимых переменных y в правой части уравнений не зависит от количества предыдущих уравнений. Поэтому для системы (2) правильным вариантом ответа является система 
(3) – является системой рекурсивных уравнений. В такой системе в правой части уравнений стоят как зависимые переменные y, так и независимые переменные х, при этом каждое последующее уравнение в правой части включает зависимые переменные y только предыдущих уравнений системы. Поэтому для системы (3) правильным вариантом ответа является система 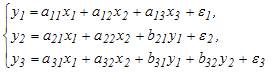
Система  содержит ошибку, так как в правой части всех уравнений системы стоит переменная у1. Поэтому данная система не может быть отнесена ни к одному из классов систем эконометрических уравнений, это неправильный вариант ответа.
содержит ошибку, так как в правой части всех уравнений системы стоит переменная у1. Поэтому данная система не может быть отнесена ни к одному из классов систем эконометрических уравнений, это неправильный вариант ответа.
 ЗАДАНИЕ N 11 сообщить об ошибке
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Идентификация систем эконометрических уравнений
Модель мультипликатора-акселератора Кейнса

где C – личное потребление в постоянных ценах,
y – национальный доход в постоянных ценах,
I – инвестиции в постоянных ценах,
 – случайная составляющая,
– случайная составляющая,
Установите соответствие:
(1) эндогенная переменная
(2) экзогенные переменная.
|
|
|
| y – национальный доход в постоянных ценах
|
|
|
|
| I – инвестиции в постоянных ценах
|
|
|
|
|  – случайная составляющая – случайная составляющая
|
Решение:
В модели мультипликатора-акселератора Кейнса эндогенными переменные являются переменные C (личное потребление в постоянных ценах) и y (национальный доход в постоянных ценах). А экзогенными переменными является только переменная I (инвестиции в постоянных ценах). И  является случайной составляющей.
является случайной составляющей.
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С.341–355.
 ЗАДАНИЕ N 12 сообщить об ошибке
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Методы оценки параметров систем одновременных уравнений: косвенный метод наименьших квадратов (КМНК) и двухшаговый метод наименьших квадратов (ДМНК)
Система независимых эконометрических уравнений может быть идентифицирована с помощью обычного метода наименьших квадратов. Определите последовательность этапов алгоритма оценки параметров для такой модели.
|
|
|
| оценка возможности идентификации модели как системы независимых уравнений
|
|
|
|
| разделение системы независимых уравнений на отдельные уравнения регрессии
|
|
|
|
| построение общего вида системы нормальных уравнений для каждого уравнения системы и расчет необходимых значений сумм
|
|
|
|
| решение системы нормальных уравнений для каждого уравнения системы
|
|
|
|
| подстановка найденных значений оценок параметров в уравнения системы
|
 ЗАДАНИЕ N 13 сообщить об ошибке
ЗАДАНИЕ N 13 сообщить об ошибке
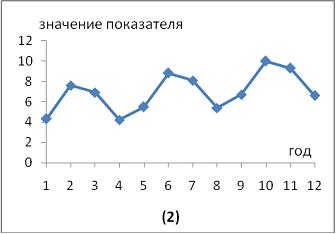
Тема: Временные ряды данных: характеристики и общие понятия
Изображенный на рисунке временной ряд содержит следующие компоненты:


|
|
| возрастающую тенденцию и сезонную компоненту
|
|
|
|
| тенденцию и возрастающую сезонную компоненту
|
|
|
|
| убывающую тенденцию и возрастающую сезонную компоненту
|
|
|
|
| возрастающую тенденцию и возрастающую сезонную компоненту
|
 ЗАДАНИЕ N 14 сообщить об ошибке
ЗАДАНИЕ N 14 сообщить об ошибке
Тема: Аддитивная и мультипликативная модели временных рядов
Уровень временного ряда (yt) формируется под воздействием различных факторов – компонент: Т (тенденция), S (циклические и/или сезонные колебания), Е (случайные факторы). Мультипликативную модель временного ряда не формируют следующие значения компонент уровня временного ряда …

|
|
| yt = 7; T = -3,5; S = -2; E = -1
|
|
|
|
| yt = 7; T = 7; S = 1; E = 1
|
|
|
|
| yt = 7; T = 3,5; S = 2; E = 1
|
|
|
|
| yt = 7; T = 3,5; S = -2; E = -1
|
 ЗАДАНИЕ N 15 сообщить об ошибке
ЗАДАНИЕ N 15 сообщить об ошибке
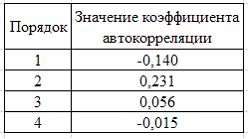
Тема: Структура временного ряда
Данная таблица значений автокорреляционной функции соответствует структуре временного ряда …
 ЗАДАНИЕ N 16 сообщить об ошибке
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Модели стационарных и нестационарных временных рядов и их идентификация
Для временного ряда известны характеристики:  – среднее и
– среднее и 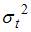 – дисперсия. Если временной ряд является стационарным, то …
– дисперсия. Если временной ряд является стационарным, то …
 ЗАДАНИЕ N 17 сообщить об ошибке
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Оценка параметров линейных уравнений регрессии
Для построения эконометрической модели линейного уравнения регрессии используется таблица статистических данных.

При помощи метода наименьших квадратов (МНК) рассчитываются оценки параметров модели вида  . Для выборочного i -го наблюдения модель имеет вид
. Для выборочного i -го наблюдения модель имеет вид  . При применении метода наименьших квадратов рассчитывается …
. При применении метода наименьших квадратов рассчитывается …
 ЗАДАНИЕ N 18 сообщить об ошибке
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Обобщенный метод наименьших квадратов (ОМНК)
Пусть y – издержки производства, 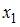 – объем продукции,
– объем продукции, 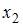 – основные производственные фонды,
– основные производственные фонды,  – численность работников. Известно, что в уравнении
– численность работников. Известно, что в уравнении  дисперсии остатков пропорциональны квадрату объема продукции
дисперсии остатков пропорциональны квадрату объема продукции  .
.
Применим обобщенный метод наименьших квадратов, поделив обе части уравнения на  После применения обобщенного метода наименьших квадратов новая модель приняла вид
После применения обобщенного метода наименьших квадратов новая модель приняла вид  . Тогда параметр
. Тогда параметр  в новом уравнении характеризует среднее изменение затрат на единицу продукции при увеличении …
в новом уравнении характеризует среднее изменение затрат на единицу продукции при увеличении …

|
|
| фондоемкости продукции при неизменном уровне трудоемкости продукции
|
|
|
|
| трудоемкости продукции при неизменном уровне фондоемкости продукции
|
|
|
|
| производительности труда при неизменном уровне фондовооруженности труда
|
|
|
|
| фондовооруженности труда при неизменном уровне производительности труда
|
Решение:
Пусть y – издержки производства, 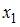 – объем продукции,
– объем продукции, 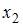 – основные производственные фонды,
– основные производственные фонды,  – численность работников. Известно, что в уравнении
– численность работников. Известно, что в уравнении  дисперсии остатков пропорциональны квадрату объема продукции
дисперсии остатков пропорциональны квадрату объема продукции  .
.
После применения обобщенного метода наименьших квадратов новая модель приняла вид  . Новая модель имеет дело с новыми переменными
. Новая модель имеет дело с новыми переменными 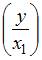 – затраты на единицу продукции,
– затраты на единицу продукции,  – фондоемкость продукции,
– фондоемкость продукции,  – трудоемкость продукции. В новой модели параметр
– трудоемкость продукции. В новой модели параметр  показывает среднее изменение затрат на единицу продукции
показывает среднее изменение затрат на единицу продукции 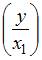 с увеличением на единицу фондоемкости продукции
с увеличением на единицу фондоемкости продукции  при неизменном уровне трудоемкости продукции
при неизменном уровне трудоемкости продукции  .
.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 206.
 ЗАДАНИЕ N 19 сообщить об ошибке
ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Предпосылки МНК, методы их проверки
Из перечисленного условием выполнения предпосылок метода наименьших квадратов не является ____ остатков.

|
|
| гетероскедатичность
|
|
|
|
| случайный характер
|
|
|
|
| нулевая средняя величина
|
|
|
|
| отсутствие автокорреляции
|
Решение:
Условия, необходимые для несмещенных, состоятельных и эффективных оценок, представляют собой предпосылки МНК.
Исследования остатков предполагают проверку наличия следующих пяти предпосылок МНК:
– случайный характер остатков;
– нулевая средняя величина остатков, не зависящая от  ;
;
– гомоскедастичность остатков;
– отсутствие автокорреляции остатков;
– подчинение остатков нормальному закону распределения.
Гетероскедатичность остатков не является предпосылкой МНК.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С.184–186.
Бывшев В.А. Эконометрика: учеб. пособие / В.А. Бывшев. – М.: Финансы и статистика, 2008. – С.268–301.
 ЗАДАНИЕ N 20 сообщить об ошибке
ЗАДАНИЕ N 20 сообщить об ошибке
Тема: Свойства оценок параметров эконометрической модели, получаемых при помощи МНК
Пусть  – оценка параметра
– оценка параметра  регрессионной модели, полученная с помощью метода наименьших квадратов;
регрессионной модели, полученная с помощью метода наименьших квадратов;  – математическое ожидание оценки
– математическое ожидание оценки  . В том случае если
. В том случае если  , то оценка обладает свойством …
, то оценка обладает свойством …

|
|
| несмещенности
|
|
|
|
| состоятельности
|
|
|
|
| эффективности
|
|
|
|
| смещенности
|
 ЗАДАНИЕ N 21 сообщить об ошибке
ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Фиктивные переменные
Эконометрическое моделирование зависимости по неоднородной совокупности данных может осуществляться на основе …

|
|
| использования фиктивных переменных
|

|
|
| разделения неоднородной совокупности данных на однородные
|
|
|
|
| использования стандартизованных переменных
|
|
|
|
| неоднородных статистических гипотез
|
Решение:
Одним из типов эконометрических моделей является уравнение регрессии, которое может быть записано в виде математического выражения  , где y – зависимая переменная, xj – независимая переменная (j = 1,…, k; k – количество независимых переменных), f – тип функциональной зависимости (математическая функция),
, где y – зависимая переменная, xj – независимая переменная (j = 1,…, k; k – количество независимых переменных), f – тип функциональной зависимости (математическая функция),  – случайные факторы. Данное уравнение является наглядным примером количественного выражения взаимосвязей социально-экономических показателей.
– случайные факторы. Данное уравнение является наглядным примером количественного выражения взаимосвязей социально-экономических показателей.
При построении регрессионной модели может возникнуть ситуация, когда необходимо включить в уравнение помимо количественных переменных переменные, отражающие некоторые атрибутивные признаки (пол, образование, регион и т.п.). Такого рода качественные переменные называются «фиктивными» (dummy) переменными. Они отражают неоднородность исследуемой статистической совокупности и используются для более качественного моделирования зависимостей в таких неоднородных объектах наблюдения. Однако, в некоторых случаях можно рекомендовать разделить неоднородную совокупность данных на однородные и применять методы моделирования к отдельным однородным совокупностям данных. Поэтому правильными вариантами являются ответы: «использования фиктивных переменных» и «разделения неоднородной совокупности на однородные». Вариант «использование стандартизованных переменных» не является верным, так как стандартизованные переменные используются для приведения уравнения в естественном масштабе к стандартизованному уравнению регрессии с бета-коэффициентами (стандартизованными коэффициентами регрессии). Вариант ответа «неоднородных статистических гипотез» не несет в себе смысловой нагрузки, поэтому тоже не является правильным.
 ЗАДАНИЕ N 22 сообщить об ошибке
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Спецификация эконометрической модели
В модели вида  количество объясняющих переменных равно …
количество объясняющих переменных равно …
 ЗАДАНИЕ N 23 сообщить об ошибке
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Отбор факторов, включаемых в модель множественной регрессии
Для эконометрической модели линейного уравнения множественной регрессии вида  построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х(1), х(2), х(3) – независимые переменные):
построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х(1), х(2), х(3) – независимые переменные):

Коллинеарными (тесносвязанными) независимыми (объясняющими) переменными являются …

|
|
| x(1) и x(2)
|
|
|
|
| y и x(3)
|
|
|
|
| x(1) и x(3)
|
|
|
|
| x(2) и x(3)
|
 ЗАДАНИЕ N 24 сообщить об ошибке
ЗАДАНИЕ N 24 сообщить об ошибке
Тема: Линейное уравнение множественной регрессии
Известно, что доля остаточной дисперсии зависимой переменной в ее общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …



 эВ, где
эВ, где  . При переходе из некоторого состояния
. При переходе из некоторого состояния  на уровень энергии E 2 атом испускает фотон с длиной волны
на уровень энергии E 2 атом испускает фотон с длиной волны  нм. Какой номер имеет состояние n, из которого перешел атом? Какую длину имела бы волна при переходе атома в состояние E 1?
нм. Какой номер имеет состояние n, из которого перешел атом? Какую длину имела бы волна при переходе атома в состояние E 1?
 ЗАДАНИЕ N 2 сообщить об ошибке
ЗАДАНИЕ N 2 сообщить об ошибке



 является нелинейным по переменной х, но линейным по параметрам. Уравнения
является нелинейным по переменной х, но линейным по параметрам. Уравнения  и
и  также являются нелинейными по переменной х, но линейными по параметрам. Поэтому правильный вариант ответа – «
также являются нелинейными по переменной х, но линейными по параметрам. Поэтому правильный вариант ответа – « может быть применен метод …
может быть применен метод …
 (см. рис.).
(см. рис.).
 является …
является … будет [–1; 0].
будет [–1; 0]. и спрос
и спрос 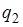 являются линейными функциями цены p, состоит из уравнений …
являются линейными функциями цены p, состоит из уравнений …
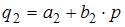


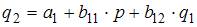


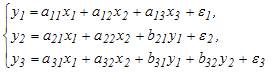


 содержит ошибку, так как в правой части всех уравнений системы стоит переменная у1. Поэтому данная система не может быть отнесена ни к одному из классов систем эконометрических уравнений, это неправильный вариант ответа.
содержит ошибку, так как в правой части всех уравнений системы стоит переменная у1. Поэтому данная система не может быть отнесена ни к одному из классов систем эконометрических уравнений, это неправильный вариант ответа.
 – случайная составляющая,
– случайная составляющая,




 – среднее и
– среднее и 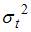 – дисперсия. Если временной ряд является стационарным, то …
– дисперсия. Если временной ряд является стационарным, то …
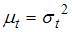

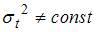

 . Для выборочного i -го наблюдения модель имеет вид
. Для выборочного i -го наблюдения модель имеет вид  . При применении метода наименьших квадратов рассчитывается …
. При применении метода наименьших квадратов рассчитывается …

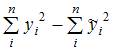

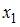 – объем продукции,
– объем продукции, 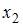 – основные производственные фонды,
– основные производственные фонды,  – численность работников. Известно, что в уравнении
– численность работников. Известно, что в уравнении  дисперсии остатков пропорциональны квадрату объема продукции
дисперсии остатков пропорциональны квадрату объема продукции  .
. После применения обобщенного метода наименьших квадратов новая модель приняла вид
После применения обобщенного метода наименьших квадратов новая модель приняла вид  . Тогда параметр
. Тогда параметр  в новом уравнении характеризует среднее изменение затрат на единицу продукции при увеличении …
в новом уравнении характеризует среднее изменение затрат на единицу продукции при увеличении …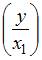 – затраты на единицу продукции,
– затраты на единицу продукции,  – фондоемкость продукции,
– фондоемкость продукции,  – трудоемкость продукции. В новой модели параметр
– трудоемкость продукции. В новой модели параметр  показывает среднее изменение затрат на единицу продукции
показывает среднее изменение затрат на единицу продукции  ;
; – оценка параметра
– оценка параметра  регрессионной модели, полученная с помощью метода наименьших квадратов;
регрессионной модели, полученная с помощью метода наименьших квадратов;  – математическое ожидание оценки
– математическое ожидание оценки  , то оценка обладает свойством …
, то оценка обладает свойством … , где y – зависимая переменная, xj – независимая переменная (j = 1,…, k; k – количество независимых переменных), f – тип функциональной зависимости (математическая функция),
, где y – зависимая переменная, xj – независимая переменная (j = 1,…, k; k – количество независимых переменных), f – тип функциональной зависимости (математическая функция),  – случайные факторы. Данное уравнение является наглядным примером количественного выражения взаимосвязей социально-экономических показателей.
– случайные факторы. Данное уравнение является наглядным примером количественного выражения взаимосвязей социально-экономических показателей. количество объясняющих переменных равно …
количество объясняющих переменных равно … построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х(1), х(2), х(3) – независимые переменные):
построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х(1), х(2), х(3) – независимые переменные): 





