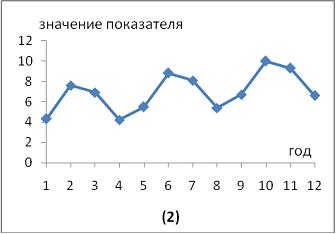
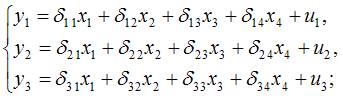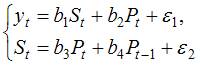Ряд, уровни которого образуются как сумма среднего уровня ряда и некоторой случайной компоненты, изображен на графике …
Решение:
График ряда, уровни которого образуются как сумма среднего уровня ряда и некоторой случайной компоненты, будет колебаться относительно своего среднего значения.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 296–300.
Эконометрика: учеб. / под ред. Д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С.284–290.
 ЗАДАНИЕ N 2 сообщить об ошибке
ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Структура временного ряда
Данная таблица значений автокорреляционной функции соответствует структуре временного ряда …

 ЗАДАНИЕ N 3 сообщить об ошибке
ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Аддитивная и мультипликативная модели временных рядов
Уровень временного ряда (yt) формируется под воздействием различных факторов – компонент: Т (тенденция), S (циклические и/или сезонные колебания), Е (случайные факторы). Для аддитивной модели временного ряда для уровня y3 получено уравнение тренда T = 3,14 + 2,07t. Известны значения компонент: S3 = 1,6; E3 = –0,3. Тогда значение уровня временного ряда y3 будет равно …

|
|
| 10,65
|
|
|
|
| 9,35
|
|
|
|
| 1,3
|
|
|
|
| 6,51
|
Решение:
Аддитивная модель временного ряда записывается в виде выражения  и предполагает, что сумма компонент ряда T, S и Е равна значению уровня ряда yt. Расчет компоненты Т осуществим по формуле T = 3,14 + 2,07t, где t = 3, так как необходимо рассчитать значение уровня y3.
и предполагает, что сумма компонент ряда T, S и Е равна значению уровня ряда yt. Расчет компоненты Т осуществим по формуле T = 3,14 + 2,07t, где t = 3, так как необходимо рассчитать значение уровня y3.
Получаем: y3 = 3,14 + 2,07 * 3 +1,6 + (–0,3) = 10,65.
Бывшев, В.А. Эконометрика: учеб. пособие / В.А. Бывшев. – М.: Финансы и статистика, 2008. – С. 236 –237.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 311 –313.
 ЗАДАНИЕ N 4 сообщить об ошибке
ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Модели стационарных и нестационарных временных рядов и их идентификация
Процесс «белый шум» является _______ временным рядом.

|
|
| стационарным
|
|
|
|
| нестационарным
|
|
|
|
| детерминированным
|
|
|
|
| неслучайным
|
 ЗАДАНИЕ N 5 сообщить об ошибке
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Оценка качества нелинейных уравнений регрессии
Для нелинейного уравнения регрессии рассчитано значение индекса детерминации  . Следовательно, доля объясненной дисперсии в общей дисперсии зависимой переменной для данного уравнения составляет …
. Следовательно, доля объясненной дисперсии в общей дисперсии зависимой переменной для данного уравнения составляет …

|
|
| 0,6
|
|
|
|
| 0,6%
|
|
|
|
| 0,4
|
|
|
|
| 0,4%
|
Решение:
Уравнение регрессии строится для моделирования зависимой переменной. При этом общая дисперсия зависимой переменной принимается как целое, то есть за 1. Она (1 – общая дисперсия) раскладывается на две части: объясненная уравнением часть и не объясненная уравнением (остаточная) часть. Для каждой части рассчитывается ее доля в общей дисперсии, то есть в 1. Доля объясненной дисперсии в общей есть не что иное как индекс детерминации (для нелинейных уравнений) или коэффициент детерминации (для линейных уравнений), обозначается R2. Доля остаточной дисперсии в общей рассчитывается как разность (1– R2). Доля каждой из частей всегда не больше 1; доля есть часть, поэтому не имеет единицы измерения. Можно рассчитать также процент, тогда долю нужно умножить на 100%, это значение будет показывать, сколько процентов занимает та или иная часть дисперсии (объясненная или остаточная) в общей дисперсии, то есть в 100%. В нашем случае  , следовательно, доля объясненной дисперсии зависимой переменной в ее общей дисперсии составляет 0,6 (это правильный вариант ответа); доля остаточной дисперсии зависимой переменной в общей составляет 0,4. В процентном соотношении получаем: доля объясненной дисперсии зависимой переменной в ее общей дисперсии составляет 60%; доля остаточной дисперсии зависимой переменной в общей составляет 40%.
, следовательно, доля объясненной дисперсии зависимой переменной в ее общей дисперсии составляет 0,6 (это правильный вариант ответа); доля остаточной дисперсии зависимой переменной в общей составляет 0,4. В процентном соотношении получаем: доля объясненной дисперсии зависимой переменной в ее общей дисперсии составляет 60%; доля остаточной дисперсии зависимой переменной в общей составляет 40%.
Поэтому правильный вариант ответа «0,6».
 ЗАДАНИЕ N 6 сообщить об ошибке
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Линеаризация нелинейных моделей регрессии
Для линеаризации нелинейной регрессионной модели 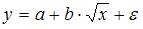 используется замена …
используется замена …
Решение:
Линеаризация – процедура приведения нелинейной регрессионной модели к линейному виду путем различных математических преобразований. Это необходимо для обеспечения возможности использования метода наименьших квадратов, позволяющего оценить параметры линейных уравнений регрессии. В качестве одного из способов линеаризации используется замена переменных. Уравнение 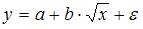 может быть линеаризовано заменой
может быть линеаризовано заменой  , в результате получаем модель линейного уравнения парной регрессии
, в результате получаем модель линейного уравнения парной регрессии 
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 85.
 ЗАДАНИЕ N 7 сообщить об ошибке
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Нелинейные зависимости в экономике
Нелинейное уравнение парной регрессии вида  является _____ моделью.
является _____ моделью.

|
|
| гиперболической
|
|
|
|
| полиномиальной
|
|
|
|
| степенной
|
|
|
|
| показательной
|
 ЗАДАНИЕ N 8 сообщить об ошибке
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Виды нелинейных уравнений регрессии
Среди предложенных нелинейных зависимостей нелинейной по параметрам является …
Решение:
Среди предложенных нелинейных зависимостей зависимость 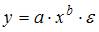 является нелинейной по параметрам, но внутренне линейной, поскольку с помощью логарифмирования ее можно привести к линейному виду. Остальные функции линейны по параметрам, но нелинейны относительно переменных и к линейному виду могут быть приведены с помощью замены переменных.
является нелинейной по параметрам, но внутренне линейной, поскольку с помощью логарифмирования ее можно привести к линейному виду. Остальные функции линейны по параметрам, но нелинейны относительно переменных и к линейному виду могут быть приведены с помощью замены переменных.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 96–99.
Бывшев В.А. Эконометрика: учеб. пособие / В.А. Бывшев. – М.: Финансы и статистика, 2008. – С.331–346.
 ЗАДАНИЕ N 9 сообщить об ошибке
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Отбор факторов, включаемых в модель множественной регрессии
Для эконометрической модели линейного уравнения множественной регрессии вида  построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х(1), х(2), х(3), x(4) – независимые переменные):
построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х(1), х(2), х(3), x(4) – независимые переменные):

Коллинеарными (тесно связанными) независимыми (объясняющими) переменными не являются …

|
|
| x(2) и x(3)
|
|
|
|
| x(1) и x(3)
|
|
|
|
| x(1) и x(4)
|
|
|
|
| x(2) и x(4)
|
Решение:
При построении модели множественной регрессии необходимо исключить возможность существования тесной линейной зависимости между независимыми (объясняющими) переменными, которая ведет к проблеме мультиколлинеарности. При этом осуществляют проверку коэффициентов линейной корреляции для каждой пары независимых (объясняющих) переменных. Эти значения отражены в матрице парных коэффициентов линейной корреляции. Считается, что наличие значений коэффициентов парной корреляции между объясняющими переменными, превышающих по абсолютной величине 0,7, отражает тесную связь между этими переменными (теснота связи с переменной y в данном случае не рассматривается). Такие независимые переменные называются коллинеарными. Если значение коэффициента парной корреляции между объясняющими переменными не превышает по абсолютной величине 0,7, то такие объясняющие переменные не являются коллинеарными. Рассмотрим значения парных коэффициентов межфакторной корреляции: между x(1) и x(2) значение равно 0,45; между x(1) и x(3) – равно 0,82; между x(1) и x(4) – равно 0,94; между x(2) и x(3) – равно 0,3; между x(2) и x(4) – равно 0,7; между x(3) и x(4) – равно 0,12. Таким образом, не превышают 0,7 значения 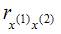 ,
,  ,
,  . Следовательно, коллинеарными не являются факторы x(1) и x(2), x(2) и x(3), x(3) и x(4). Из последних перечисленных пар в вариантах ответов присутствует пара x(2) и x(3) – это верный вариант ответа. Для остальных пар: x(1 и x(3), x(1) и x(4), x(2) и x(4) – значения парных коэффициентов межфакторной корреляции превышают 0,7, и эти факторы являются коллинеарными.
. Следовательно, коллинеарными не являются факторы x(1) и x(2), x(2) и x(3), x(3) и x(4). Из последних перечисленных пар в вариантах ответов присутствует пара x(2) и x(3) – это верный вариант ответа. Для остальных пар: x(1 и x(3), x(1) и x(4), x(2) и x(4) – значения парных коэффициентов межфакторной корреляции превышают 0,7, и эти факторы являются коллинеарными.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 110–119.
Эконометрика: учеб. / под ред. И.И. Елисеевой. – М.: Проспект, 2009. – С. 35–41.
 ЗАДАНИЕ N 10 сообщить об ошибке
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Спецификация эконометрической модели
Эконометрическая модель уравнения регрессии может включать одну или несколько независимых переменных. По данному классификационному признаку различают _______ регрессию.

|
|
| простую и множественную
|
|
|
|
| линейную и нелинейную
|
|
|
|
| множественную и многофакторную
|
|
|
|
| простую и парную
|
Решение:
Эконометрическая модель уравнения регрессии может быть представлена выражением 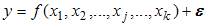 , где y – зависимая переменная, xj – независимая переменная (j = 1,…, k; k – количество независимых переменных), f – тип функциональной зависимости (математическая функция),
, где y – зависимая переменная, xj – независимая переменная (j = 1,…, k; k – количество независимых переменных), f – тип функциональной зависимости (математическая функция),  – случайные факторы. Спецификация эконометрической модели уравнения регрессии определяется видом функции f, а также числом независимых переменных (факторов или регрессоров). Парная и множественная регрессия характеризуют количество независимых переменных хj в уравнении регрессии (парная – одна независимая переменная; множественная – не меньше двух независимых переменных). Поэтому верным вариантом является «простую и множественную» регрессии. Вариант ответа «линейную и нелинейную» – неверный, так как это характеризует вид зависимости (математической функции) f. Варианты «множественную и многофакторную» и «простую и парную» отражают один из классификационных признаков и не описывают всей совокупности эконометрических моделей регрессии.
– случайные факторы. Спецификация эконометрической модели уравнения регрессии определяется видом функции f, а также числом независимых переменных (факторов или регрессоров). Парная и множественная регрессия характеризуют количество независимых переменных хj в уравнении регрессии (парная – одна независимая переменная; множественная – не меньше двух независимых переменных). Поэтому верным вариантом является «простую и множественную» регрессии. Вариант ответа «линейную и нелинейную» – неверный, так как это характеризует вид зависимости (математической функции) f. Варианты «множественную и многофакторную» и «простую и парную» отражают один из классификационных признаков и не описывают всей совокупности эконометрических моделей регрессии.
 ЗАДАНИЕ N 11 сообщить об ошибке
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Линейное уравнение множественной регрессии
В эконометрической модели линейного уравнения регрессии  переменной(-ыми) является(-ются) …
переменной(-ыми) является(-ются) …

|
|
| y, xj
|
|
|
|
| a
|
|
|
|
| bj
|
|
|
|
| 
|
Решение:
Эконометрическая модель линейного уравнения регрессии имеет вид  , где y – зависимая переменная, xj – независимая переменная (
, где y – зависимая переменная, xj – независимая переменная ( – номер независимой переменной в модели, k – общее количество независимых переменных в модели); a, bj – параметры уравнения;
– номер независимой переменной в модели, k – общее количество независимых переменных в модели); a, bj – параметры уравнения; 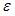 – ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Таким образом, верным ответом является «y, xj».
– ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Таким образом, верным ответом является «y, xj».
 ЗАДАНИЕ N 12 сообщить об ошибке
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Фиктивные переменные
Дана таблица исходных данных для построения эконометрической регрессионной модели:

Фиктивными переменными не являются …

|
|
| стаж работы
|

|
|
| производительность труда
|
|
|
|
| уровень образования
|
|
|
|
| уровень квалификации работника
|
 ЗАДАНИЕ N 13 сообщить об ошибке
ЗАДАНИЕ N 13 сообщить об ошибке
Тема: Свойства оценок параметров эконометрической модели, получаемых при помощи МНК
Если оценка параметра является смещенной, то нарушается предпосылка метода наибольших квадратов о _____ остатков.

|
|
| нулевой средней величине
|
|
|
|
| нормальном законе распределения
|
|
|
|
| случайном характере
|
|
|
|
| гомоскедастичности
|
Решение:
Оценка называется несмещенной, если математическое ожидание остатков равно нулю. Если оценка параметров регрессии является смещенной, то математическое ожидание остатков отличается от нуля, и при большом количестве выборочных оцениваний остатки будут накапливаться.
Нарушается предпосылка о нулевой средней величине остатков.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 60.
 ЗАДАНИЕ N 14 сообщить об ошибке
ЗАДАНИЕ N 14 сообщить об ошибке
Тема: Обобщенный метод наименьших квадратов (ОМНК)
Обобщенный метод наименьших квадратов не может применяться для оценки параметров линейных регрессионных моделей в случае, если …

|
|
| средняя величина остатков не равна нулю
|
|
|
|
| остатки гетероскедастичны
|
|
|
|
| остатки автокоррелированны
|
|
|
|
| дисперсия остатков не является постоянной величиной
|
 ЗАДАНИЕ N 15 сообщить об ошибке
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Предпосылки МНК, методы их проверки
Известно, что коэффициент автокорреляции остатков первого порядка равен –0,3. Также даны критические значения статистики Дарбина – Уотсона для заданного количества параметров при неизвестном и количестве наблюдений  ,
,  . По данным характеристикам можно сделать вывод о том, что …
. По данным характеристикам можно сделать вывод о том, что …

|
|
| автокорреляция остатков отсутствует
|
|
|
|
| статистика Дарбина – Уотсона попадает в зону неопределенности
|
|
|
|
| есть положительная автокорреляция остатков
|
|
|
|
| есть отрицательная автокорреляция остатков
|
Решение:
Дано, что коэффициент автокорреляции остатков первого порядка равен –0,3,  . Рассчитаем статистику Дарбина – Уотсона по формуле
. Рассчитаем статистику Дарбина – Уотсона по формуле  . Нам известны критические значения статистики Дарбина – Уотсона для заданного количества параметров при неизвестном и количестве наблюдений
. Нам известны критические значения статистики Дарбина – Уотсона для заданного количества параметров при неизвестном и количестве наблюдений  ,
,  , которые разбивают отрезок от 0 до 4 на пять частей.
, которые разбивают отрезок от 0 до 4 на пять частей.
В интервале [0; 0,82] есть положительная автокорреляция остатков;
в интервале (0,82; 1,32] – зона неопределенности;
в интервале (1,32; 2,68] нет автокорреляции остатков;
в интервале (2,68; 3,12] – зона неопределенности;
в интервале (3,12; 4] есть отрицательная автокорреляция остатков.
В нашем случае значение статистики Дарбина–Уотсона d=2,6 попадает в интервал (1,32; 2,68]. Значит, можно сделать вывод, что нет автокорреляции остатков.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С.438-442, 186-197.
Бывшев В.А. Эконометрика: учеб. пособие / В.А. Бывшев. – М.: Финансы и статистика, 2008. – С.268–301.
 ЗАДАНИЕ N 16 сообщить об ошибке
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Оценка параметров линейных уравнений регрессии
Метод наименьших квадратов (МНК) может применяться для оценки параметров исходной регрессионной модели в _________ форме.

|
|
| линейной
|
|
|
|
| нелинейной
|
|
|
|
| экспоненциальной
|
|
|
|
| нормальной
|
Решение:
Одним из типов эконометрических моделей является уравнение регрессии, которое может быть записано в виде математического выражения  , где y – зависимая переменная, xj – независимая переменная (j = 1,…, k; k – количество независимых переменных), f – тип функциональной зависимости (математическая функция),
, где y – зависимая переменная, xj – независимая переменная (j = 1,…, k; k – количество независимых переменных), f – тип функциональной зависимости (математическая функция),  – случайные факторы.
– случайные факторы.
Метод наименьших квадратов (МНК) применяется для оценки параметров линейных регрессионных моделей (f – линейная математическая функция). Поэтому правильный вариант ответа – «в линейной форме». При применении МНК к нелинейным уравнениям, в том числе и к экспоненциальным, исходную модель линеаризуют и МНК применяют к линеаризованной модели, к исходной нелинейной модели МНК не применяют. Поэтому варианты ответов – «в нелинейной форме» и в «экспоненциальной форме» неверные. При применении МНК оценки параметров находят на основе системы нормальных уравнений, в которой неизвестными величинами являются искомые значения оценок параметров, но исходная модель должна являться линейной. Вариант ответа «в нормальной форме» не является правильным, а только может ассоциироваться с понятием «система нормальных уравнений МНК».
 ЗАДАНИЕ N 17 сообщить об ошибке
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Оценка значимости параметров эконометрической модели
В уравнении множественной регрессии, построенном на основании 14 наблюдений, 
в скобках указаны значения t -статистик, соответствующие параметрам регрессии. Также известны критические значения Стьюдента для 10 степеней свободы при различных уровнях значимости  ,
,  ,
,  . Для данного уравнения при уровне значимости α=0,01 значимым(-ыми) является(-ются) параметр(-ы) …
. Для данного уравнения при уровне значимости α=0,01 значимым(-ыми) является(-ются) параметр(-ы) …
Решение:
Чтобы оценить значимость параметров регрессии используется t -критерий Стьюдента. Для каждого коэффициента регрессии  формулируется нулевая гипотеза
формулируется нулевая гипотеза  при альтернативной гипотезе
при альтернативной гипотезе  . Затем рассчитывается фактическое значение t -статистики, которое сравнивается с критическим значением Стьюдента
. Затем рассчитывается фактическое значение t -статистики, которое сравнивается с критическим значением Стьюдента  для требуемого числа степеней свободы и уровня значимости. Если
для требуемого числа степеней свободы и уровня значимости. Если  , коэффициент
, коэффициент  значим; если
значим; если  , коэффициент
, коэффициент  незначим. В нашем случае при уровне значимости 0,01 значимым является только параметр
незначим. В нашем случае при уровне значимости 0,01 значимым является только параметр 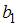 .
.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 160–170.
Кремер, Н.Ш. Эконометрика: учеб. для студентов вузов / Н. Ш. Кремер, Б. А. Путко; ред. Н. Ш. Кремер. – М.: ЮНИТИ, 2002. – С.40–52.
 ЗАДАНИЕ N 18 сообщить об ошибке
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Оценка тесноты связи
Значение коэффициента множественной корреляции рассчитывается по формуле  (
( – коэффициент множественной корреляции;
– коэффициент множественной корреляции;  – коэффициент детерминации для уравнения множественной регрессии). Тогда значение коэффициента множественной корреляции
– коэффициент детерминации для уравнения множественной регрессии). Тогда значение коэффициента множественной корреляции  будет находится в интервале …
будет находится в интервале …

|
|
| [0; 1]
|
|
|
|
| [–1; 1]
|
|
|
|
| [–1; 0]
|
|
|
|
| [0;  ] ]
|
 ЗАДАНИЕ N 19 сообщить об ошибке
ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Оценка качества подбора уравнения
Для регрессионной модели парной регрессии рассчитано значение коэффициента детерминации  . Тогда долю остаточной дисперсии зависимой переменной характеризует величина …
. Тогда долю остаточной дисперсии зависимой переменной характеризует величина …
Решение:
Значение коэффициента детерминации  характеризует долю дисперсии зависимой переменной, объясненную построенным уравнением регрессии, в общей дисперсии зависимой переменной, то есть
характеризует долю дисперсии зависимой переменной, объясненную построенным уравнением регрессии, в общей дисперсии зависимой переменной, то есть  . Разность (1 –
. Разность (1 –  ) характеризует долю остаточной дисперсии. Докажем это. Величина общей дисперсии есть сумма дисперсии зависимой переменной, которая объяснена уравнением и остаточной дисперсией. Тогда
) характеризует долю остаточной дисперсии. Докажем это. Величина общей дисперсии есть сумма дисперсии зависимой переменной, которая объяснена уравнением и остаточной дисперсией. Тогда  , или
, или  . Второе слагаемое, характеризующее долю остаточной дисперсии можно выразить:
. Второе слагаемое, характеризующее долю остаточной дисперсии можно выразить:  . Поэтому верный ответ – «
. Поэтому верный ответ – « ».
».
 ЗАДАНИЕ N 20 сообщить об ошибке
ЗАДАНИЕ N 20 сообщить об ошибке
Тема: Проверка статистической значимости эконометрической модели
Если известно уравнение множественной регрессии  построенное по результатам 50 наблюдений, для которого общая сумма квадратов отклонений равна 153, и остаточная сумма квадратов отклонений равна 3, то значение F-статистики равно …
построенное по результатам 50 наблюдений, для которого общая сумма квадратов отклонений равна 153, и остаточная сумма квадратов отклонений равна 3, то значение F-статистики равно …

|
|
| 766,67
|
|
|
|
|
|
|
|
|
| 877,45
|
|
|
|
|
|
 ЗАДАНИЕ N 21 сообщить об ошибке
ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Идентификация систем эконометрических уравнений
Модель мультипликатора-акселератора Кейнса

где C – личное потребление в постоянных ценах,
y – национальный доход в постоянных ценах,
I – инвестиции в постоянных ценах,
 – случайная составляющая,
– случайная составляющая,
Установите соответствие:
(1) эндогенная переменная
(2) экзогенные переменная.
|
|
|
| y – национальный доход в постоянных ценах
|
|
|
|
| I – инвестиции в постоянных ценах
|
|
|
|
|  – случайная составляющая – случайная составляющая
|
Решение:
В модели мультипликатора-акселератора Кейнса эндогенными переменные являются переменные C (личное потребление в постоянных ценах) и y (национальный доход в постоянных ценах). А экзогенными переменными является только переменная I (инвестиции в постоянных ценах). И  является случайной составляющей.
является случайной составляющей.
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С.341–355.
 ЗАДАНИЕ N 22 сообщить об ошибке
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Методы оценки параметров систем одновременных уравнений: косвенный метод наименьших квадратов (КМНК) и двухшаговый метод наименьших квадратов (ДМНК)
Дана система одновременных эконометрических уравнений:

Система является точно идентифицируемой. Определите последовательность этапов алгоритма оценки ее параметров.
|
|
|
| преобразование структурной формы модели в приведенную форму вида 
|
|
|
|
| оценивание параметров приведенной формы модели (приведенных коэффициентов)  для каждого уравнения приведенной формы модели обычным МНК оцениваются для каждого уравнения приведенной формы модели обычным МНК оцениваются
|
|
|
|
| трансформация коэффициентов приведенной формы модели в параметры структурной формы модели  и и 
|
|
|
|
| подстановка найденных значений коэффициентов в структурную форму системы эконометрических уравнений
|
Решение:
В случае точно идентифицируемой структурной формы модели для оценки ее параметров применяют косвенный метод наименьших квадратов (КМНК). При этом соблюдают следующую последовательность этапов КМНК:
1) структурная форма модели преобразовывается в приведенную форму модели; так как в системе 4 экзогенных переменных – (х1, х2, х3 и х4),то у правой части приведенной формы модели записывается сумма четырех произведений соответствующих коэффициентов приведенной формы и экзогенных переменных; для данной системы приведенная форма будет иметь вид
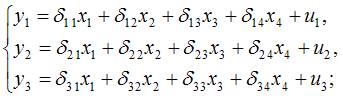
2) для каждого уравнения приведенной формы модели обычным МНК оцениваются параметры приведенной формы модели – приведенные коэффициенты  ;
;
3) коэффициенты приведенной формы модели трансформируются в параметры структурной формы модели  и
и  ;
;
4) найденные значения коэффициентов подставляются в структурную форму системы эконометрических уравнений.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 265–266.
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С. 347–353.
 ЗАДАНИЕ N 23 сообщить об ошибке
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Общие понятия о системах уравнений, используемых в эконометрике
Левая часть системы эконометрических уравнений представлена совокупностью _________ переменных.

|
|
| зависимых
|

|
|
| эндогенных
|
|
|
|
| экзогенных
|
|
|
|
| независимых
|
Решение:
Система эконометрических уравнений включает множество переменных, среди которых выделяют экзогенные и эндогенные переменные. В левой части системы эконометрических уравнений находятся только эндогенные (зависимые) переменные.
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С. 341–345.
Эконометрика: учеб. / под ред. И.И. Елисеевой. – М.: Проспект, 2009. – С. 230–233.
 ЗАДАНИЕ N 24 сообщить об ошибке
ЗАДАНИЕ N 24 сообщить об ошибке
Тема: Классификация систем уравнений
Установите соответствие между видом и классом системы эконометрических уравнений:
(1) 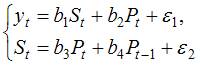
(2) 
|
|
|
| система одновременных уравнений с лаговыми переменными
|
|
|
|
| система независимых уравнений
|
|
|
|
| система одновременных уравнений без лаговых переменных
|
Решение:
Рассмотрим каждую из систем эконометрических уравнений.
В системе (1) в правой части первого уравнения стоит переменная St, которая во втором уравнении находится в левой части, следовательно, система является системой одновременных уравнений. Во втором уравнении системы (1) одновременно с переменной Pt находится лаговая переменная Pt-1, поэтому система (1) является системой одновременных уравнений с лаговыми переменными.
В системе (2) в левой части представлены переменные yt и wt, которые не входят в правую часть уравнений системы, поэтому система (2) является системой независимых уравнений.
ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Методы оценки параметров систем одновременных уравнений: косвенный метод наименьших квадратов (КМНК) и двухшаговый метод наименьших квадратов (ДМНК)
Если записать типы эконометрических моделей в следующем порядке:
1) точно идентифицируемая система одновременных уравнений,
2) сверхидентифицируемая система одновременных уравнений,
3) уравнение множественной регрессии,
4) уравнение множественной









 ЗАДАНИЕ N 3 сообщить об ошибке
ЗАДАНИЕ N 3 сообщить об ошибке и предполагает, что сумма компонент ряда T, S и Е равна значению уровня ряда yt. Расчет компоненты Т осуществим по формуле T = 3,14 + 2,07t, где t = 3, так как необходимо рассчитать значение уровня y3.
и предполагает, что сумма компонент ряда T, S и Е равна значению уровня ряда yt. Расчет компоненты Т осуществим по формуле T = 3,14 + 2,07t, где t = 3, так как необходимо рассчитать значение уровня y3. . Следовательно, доля объясненной дисперсии в общей дисперсии зависимой переменной для данного уравнения составляет …
. Следовательно, доля объясненной дисперсии в общей дисперсии зависимой переменной для данного уравнения составляет …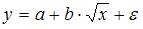 используется замена …
используется замена …




 является _____ моделью.
является _____ моделью.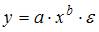



 построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х(1), х(2), х(3), x(4) – независимые переменные):
построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х(1), х(2), х(3), x(4) – независимые переменные):
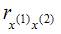 ,
,  ,
,  . Следовательно, коллинеарными не являются факторы x(1) и x(2), x(2) и x(3), x(3) и x(4). Из последних перечисленных пар в вариантах ответов присутствует пара x(2) и x(3) – это верный вариант ответа. Для остальных пар: x(1 и x(3), x(1) и x(4), x(2) и x(4) – значения парных коэффициентов межфакторной корреляции превышают 0,7, и эти факторы являются коллинеарными.
. Следовательно, коллинеарными не являются факторы x(1) и x(2), x(2) и x(3), x(3) и x(4). Из последних перечисленных пар в вариантах ответов присутствует пара x(2) и x(3) – это верный вариант ответа. Для остальных пар: x(1 и x(3), x(1) и x(4), x(2) и x(4) – значения парных коэффициентов межфакторной корреляции превышают 0,7, и эти факторы являются коллинеарными.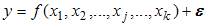 , где y – зависимая переменная, xj – независимая переменная (j = 1,…, k; k – количество независимых переменных), f – тип функциональной зависимости (математическая функция),
, где y – зависимая переменная, xj – независимая переменная (j = 1,…, k; k – количество независимых переменных), f – тип функциональной зависимости (математическая функция),  – случайные факторы. Спецификация эконометрической модели уравнения регрессии определяется видом функции f, а также числом независимых переменных (факторов или регрессоров). Парная и множественная регрессия характеризуют количество независимых переменных хj в уравнении регрессии (парная – одна независимая переменная; множественная – не меньше двух независимых переменных). Поэтому верным вариантом является «простую и множественную» регрессии. Вариант ответа «линейную и нелинейную» – неверный, так как это характеризует вид зависимости (математической функции) f. Варианты «множественную и многофакторную» и «простую и парную» отражают один из классификационных признаков и не описывают всей совокупности эконометрических моделей регрессии.
– случайные факторы. Спецификация эконометрической модели уравнения регрессии определяется видом функции f, а также числом независимых переменных (факторов или регрессоров). Парная и множественная регрессия характеризуют количество независимых переменных хj в уравнении регрессии (парная – одна независимая переменная; множественная – не меньше двух независимых переменных). Поэтому верным вариантом является «простую и множественную» регрессии. Вариант ответа «линейную и нелинейную» – неверный, так как это характеризует вид зависимости (математической функции) f. Варианты «множественную и многофакторную» и «простую и парную» отражают один из классификационных признаков и не описывают всей совокупности эконометрических моделей регрессии. переменной(-ыми) является(-ются) …
переменной(-ыми) является(-ются) … – номер независимой переменной в модели, k – общее количество независимых переменных в модели); a, bj – параметры уравнения;
– номер независимой переменной в модели, k – общее количество независимых переменных в модели); a, bj – параметры уравнения; 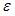 – ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Таким образом, верным ответом является «y, xj».
– ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Таким образом, верным ответом является «y, xj».
 ,
,  . По данным характеристикам можно сделать вывод о том, что …
. По данным характеристикам можно сделать вывод о том, что … . Рассчитаем статистику Дарбина – Уотсона по формуле
. Рассчитаем статистику Дарбина – Уотсона по формуле  . Нам известны критические значения статистики Дарбина – Уотсона для заданного количества параметров при неизвестном и количестве наблюдений
. Нам известны критические значения статистики Дарбина – Уотсона для заданного количества параметров при неизвестном и количестве наблюдений  , где y – зависимая переменная, xj – независимая переменная (j = 1,…, k; k – количество независимых переменных), f – тип функциональной зависимости (математическая функция),
, где y – зависимая переменная, xj – независимая переменная (j = 1,…, k; k – количество независимых переменных), f – тип функциональной зависимости (математическая функция), 
 ,
,  ,
,  . Для данного уравнения при уровне значимости α=0,01 значимым(-ыми) является(-ются) параметр(-ы) …
. Для данного уравнения при уровне значимости α=0,01 значимым(-ыми) является(-ются) параметр(-ы) …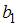



 формулируется нулевая гипотеза
формулируется нулевая гипотеза  при альтернативной гипотезе
при альтернативной гипотезе  . Затем рассчитывается фактическое значение t -статистики, которое сравнивается с критическим значением Стьюдента
. Затем рассчитывается фактическое значение t -статистики, которое сравнивается с критическим значением Стьюдента  для требуемого числа степеней свободы и уровня значимости. Если
для требуемого числа степеней свободы и уровня значимости. Если  , коэффициент
, коэффициент  , коэффициент
, коэффициент  (
( – коэффициент множественной корреляции;
– коэффициент множественной корреляции;  – коэффициент детерминации для уравнения множественной регрессии). Тогда значение коэффициента множественной корреляции
– коэффициент детерминации для уравнения множественной регрессии). Тогда значение коэффициента множественной корреляции  ]
]
 . Тогда долю остаточной дисперсии зависимой переменной характеризует величина …
. Тогда долю остаточной дисперсии зависимой переменной характеризует величина …


 характеризует долю дисперсии зависимой переменной, объясненную построенным уравнением регрессии, в общей дисперсии зависимой переменной, то есть
характеризует долю дисперсии зависимой переменной, объясненную построенным уравнением регрессии, в общей дисперсии зависимой переменной, то есть  . Разность (1 –
. Разность (1 –  , или
, или  . Второе слагаемое, характеризующее долю остаточной дисперсии можно выразить:
. Второе слагаемое, характеризующее долю остаточной дисперсии можно выразить:  . Поэтому верный ответ – «
. Поэтому верный ответ – « ».
». построенное по результатам 50 наблюдений, для которого общая сумма квадратов отклонений равна 153, и остаточная сумма квадратов отклонений равна 3, то значение F-статистики равно …
построенное по результатам 50 наблюдений, для которого общая сумма квадратов отклонений равна 153, и остаточная сумма квадратов отклонений равна 3, то значение F-статистики равно …
 – случайная составляющая,
– случайная составляющая,

 для каждого уравнения приведенной формы модели обычным МНК оцениваются
для каждого уравнения приведенной формы модели обычным МНК оцениваются
 и
и