Для мультипликативной модели временного ряда Y = T · S · E сумма скорректированных сезонных компонент равна …

|
|
| лагу
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| половине лага
|
 ЗАДАНИЕ N 2 сообщить об ошибке
ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Структура временного ряда
Автокорреляционной функцией временного ряда называется последовательность коэффициентов автокорреляции …

|
|
| первого, второго, третьего и последующих порядков
|
|
|
|
| между трендовой, сезонной и случайной компонентами
|
|
|
|
| между несколькими временными рядами
|
|
|
|
| факторов, формирующих уровень ряда
|
Решение:
Автокорреляционной функцией временного ряда называется последовательность коэффициентов автокорреляции первого, второго и последующих порядков.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 302.
 ЗАДАНИЕ N 3 сообщить об ошибке
ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Модели стационарных и нестационарных временных рядов и их идентификация
Для временного ряда известны характеристики:  – среднее и
– среднее и 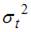 – дисперсия. Если временной ряд является стационарным, то …
– дисперсия. Если временной ряд является стационарным, то …
 ЗАДАНИЕ N 4 сообщить об ошибке
ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Временные ряды данных: характеристики и общие понятия
Изображенный на рисунке временной ряд содержит следующие компоненты:


|
|
| убывающую тенденцию и случайную компоненту
|
|
|
|
| возрастающую тенденцию и случайную компоненту
|
|
|
|
| убывающую сезонную компоненту и случайную компоненту
|
|
|
|
| сезонную компоненту и убывающую случайную компоненту
|
Решение:
Уровень временного ряда формируется под воздействием следующих компонент: тенденция, сезонная волна, циклические колебания и случайная компонента. На графике значения убывают со временем, поэтому он содержит убывающую тенденцию. Значения показателя расположены не на одной прямой линии, а несколько отклоняются, поэтому ряд имеет также случайную компоненту. Выявить сезонные колебания в данном случае нельзя, так как нельзя исследовать поведение ряда внутри каждого года. Циклических колебаний нет, так как анализ поведения ряда по графику не выявляет периодичности изменения его значений. Поэтому правильный ответ – ряд содержит убывающую тенденцию и случайную компоненту.
 ЗАДАНИЕ N 5 сообщить об ошибке
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Спецификация эконометрической модели
При идентификации модели множественной регрессии  количество оцениваемых параметров равно …
количество оцениваемых параметров равно …
Решение:
При оценке модели множественной регрессии  рассчитываются следующие параметры: свободный член a и четыре параметра при независимых переменных х. Итого 5 параметров.
рассчитываются следующие параметры: свободный член a и четыре параметра при независимых переменных х. Итого 5 параметров.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 40–50.
 ЗАДАНИЕ N 6 сообщить об ошибке
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Фиктивные переменные
Изучается зависимость цены квартиры (у) от ее жилой площади (х) и типа дома. В модель включены фиктивные переменные, отражающие рассматриваемые типы домов: монолитный, панельный, кирпичный. Получено уравнение регрессии:  ,
,
где  ,
, 
Частными уравнениями регрессии для кирпичного и монолитного являются …

|
|
|  для типа дома кирпичный для типа дома кирпичный
|

|
|
|  для типа дома монолитный для типа дома монолитный
|
|
|
|
|  для типа дома кирпичный для типа дома кирпичный
|
|
|
|
| 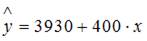 для типа дома монолитный для типа дома монолитный
|
Решение:
Требуется узнать частное уравнение регрессии для кирпичного и монолитного домов. Для кирпичного дома значения фиктивных переменных следующие  ,
,  . Уравнение примет вид:
. Уравнение примет вид:  или
или  для типа дома кирпичный.
для типа дома кирпичный.
Для монолитного дома значения фиктивных переменных следующие  ,
,  . Уравнение примет вид
. Уравнение примет вид 
или  для типа дома монолитный.
для типа дома монолитный.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 167–182.
Магнус, Ян Р. Эконометрика: нач. курс: [учеб. для студентов вузов по экон. специальностям] / Я. Р. Магнус, П. К. Катышев, А. А. Пересецкий; Акад. нар. хоз-ва при Правительстве РФ. – М.: Дело, 2005. С.190–195.
 ЗАДАНИЕ N 7 сообщить об ошибке
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Линейное уравнение множественной регрессии
Для регрессионной модели зависимости среднедушевого денежного дохода населения (руб., у) от объема валового регионального продукта (тыс. р., х1) и уровня безработицы в субъекте (%, х2) получено уравнение  . Величина коэффициента регрессии при переменной х2 свидетельствует о том, что при изменении уровня безработицы на 1% среднедушевой денежный доход ______ рубля при неизменной величине валового регионального продукта.
. Величина коэффициента регрессии при переменной х2 свидетельствует о том, что при изменении уровня безработицы на 1% среднедушевой денежный доход ______ рубля при неизменной величине валового регионального продукта.

|
|
| изменится на (-1,67)
|
|
|
|
| увеличится на 1,67
|
|
|
|
| уменьшится на (-1,67)
|
|
|
|
| изменится на 0,003
|
 ЗАДАНИЕ N 8 сообщить об ошибке
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Отбор факторов, включаемых в модель множественной регрессии
Строится эконометрическая модель линейного уравнения множественной регрессии вида  (y – зависимая переменная; х(j) – независимая переменная; j = 1,…, k; k – количество независимых переменных). При проверке независимых переменных на отсутствие мультиколлинеарности должно выполняться требование: для любых j и l
(y – зависимая переменная; х(j) – независимая переменная; j = 1,…, k; k – количество независимых переменных). При проверке независимых переменных на отсутствие мультиколлинеарности должно выполняться требование: для любых j и l  абсолютное значение парного коэффициента линейной корреляции
абсолютное значение парного коэффициента линейной корреляции  …
…

|
|
| < 0,7
|
|
|
|
| > 0,7
|
|
|
|
| = 0
|
|
|
|
|  0 0
|
Решение:
При построении модели множественной регрессии необходимо исключить возможность существования тесной линейной зависимости между независимыми переменным, что ведет к проблеме мультиколлинеарности. При этом осуществляют проверку коэффициентов линейной корреляции для каждой пары независимых (объясняющих) переменных. Эти значения отражены в матрице парных коэффициентов линейной корреляции. Считается, что наличие значений коэффициентов парной корреляции между объясняющими переменными, превышающих по абсолютной величине 0,7, отражает тесную связь между этими переменными: такие объясняющие переменные называются коллинеарными, они не должны включаться в одну модель. Поэтому верным вариантом ответа является «< 0,7».
 ЗАДАНИЕ N 9 сообщить об ошибке
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Оценка значимости параметров эконометрической модели
В уравнении множественной регрессии, построенном на основании 14 наблюдений,  в скобках указаны значения t -статистики соответствующие параметрам регрессии. Также известны критические значения Стьюдента для 10 степеней свободы для различных уровней значимости
в скобках указаны значения t -статистики соответствующие параметрам регрессии. Также известны критические значения Стьюдента для 10 степеней свободы для различных уровней значимости  ,
,  ,
, 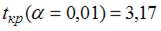 . Для данного уравнения при уровне значимости α=0,05 значимыми являются параметры …
. Для данного уравнения при уровне значимости α=0,05 значимыми являются параметры …
Решение:
Чтобы оценить значимость параметров регрессии используется t -критерий Стьюдента. Для каждого коэффициента регрессии  формулируется нулевая гипотеза
формулируется нулевая гипотеза 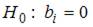 при альтернативной гипотезе
при альтернативной гипотезе  . Затем рассчитывается фактическое значение t -статистики, которое сравнивается с критическим значением Стьюдента
. Затем рассчитывается фактическое значение t -статистики, которое сравнивается с критическим значением Стьюдента  для требуемого числа степеней свободы и уровня значимости. Если
для требуемого числа степеней свободы и уровня значимости. Если  , коэффициент
, коэффициент  значим; если
значим; если  , коэффициент
, коэффициент  незначим. В нашем случае при уровне значимости 0,05 значимыми является параметры
незначим. В нашем случае при уровне значимости 0,05 значимыми является параметры  .
.
Эконометрика. Под ред. Елисеевой И.И., М.: Финансы и статистика, 2005. С.160–165.
Кремер, Н.Ш. Эконометрика: учеб. для студентов вузов / Н. Ш. Кремер, Б. А. Путко; ред. Н. Ш. Кремер. – М.: ЮНИТИ, 2002. – С.40–52.
 ЗАДАНИЕ N 10 сообщить об ошибке
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Оценка качества подбора уравнения
Для регрессионной модели вида  , где
, где 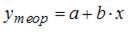 рассчитаны дисперсии:
рассчитаны дисперсии:  ;
;  ;
; 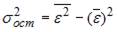 . Тогда величина коэффициента детерминации рассчитывается по формуле …
. Тогда величина коэффициента детерминации рассчитывается по формуле …
Решение:
Значение коэффициента детерминации 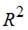 характеризует долю дисперсии зависимой переменной, объясненную построенным уравнением регрессии, в общей дисперсии зависимой переменной, то есть
характеризует долю дисперсии зависимой переменной, объясненную построенным уравнением регрессии, в общей дисперсии зависимой переменной, то есть  .
.
 ЗАДАНИЕ N 11 сообщить об ошибке
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Оценка тесноты связи
Для регрессионной модели вида  показателем тесноты связи является …
показателем тесноты связи является …

|
|
| коэффициент множественной корреляции
|
|
|
|
| парный коэффициент корреляции
|
|
|
|
| коэффициент автокорреляции
|
|
|
|
| F-критерий Фишера
|
Решение:
Заданная регрессионная модель – это линейное уравнение множественной регрессии, для которого показателем тесноты связи является коэффициент множественной корреляции, характеризующий связь между зависимой переменной y и совокупностью независимых переменных  . Верный вариант – «коэффициент множественной корреляции». Вариант «парный коэффициент корреляции» неверный, так как в данном случае рассматривается уравнение множественной регрессии. Вариант «коэффициент автокорреляции» неверный, так как автокорреляция предполагает исследование тесноты связи внутри одного ряда. Вариант «F-критерий Фишера» неверный, так как данный показатель используется для оценки существенности связи и значимости построенного уравнения, но не для оценки тесноты связи.
. Верный вариант – «коэффициент множественной корреляции». Вариант «парный коэффициент корреляции» неверный, так как в данном случае рассматривается уравнение множественной регрессии. Вариант «коэффициент автокорреляции» неверный, так как автокорреляция предполагает исследование тесноты связи внутри одного ряда. Вариант «F-критерий Фишера» неверный, так как данный показатель используется для оценки существенности связи и значимости построенного уравнения, но не для оценки тесноты связи.
 ЗАДАНИЕ N 12 сообщить об ошибке
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Проверка статистической значимости эконометрической модели
Для совокупности из n единиц наблюдений построена модель линейного уравнения множественной регрессии с количеством параметров при независимых переменных, равным k. Тогда при расчете объясненной дисперсии на одну степень свободы величину дисперсии относят к значению …

|
|
| k
|
|
|
|
| k + 1
|
|
|
|
| k – 1
|
|
|
|
| n + k
|
 ЗАДАНИЕ N 13 сообщить об ошибке
ЗАДАНИЕ N 13 сообщить об ошибке
Тема: Линеаризация нелинейных моделей регрессии
При линеаризации нелинейных регрессионных моделей как один из видов преобразований используется логарифмирование уравнения. Указанным способом не может быть линеаризовано уравнение …
Решение:
Линеаризация – это процедура приведения нелинейной регрессионной модели к линейному виду путем различных математических преобразований. Это необходимо для обеспечения возможности использования метода наименьших квадратов, позволяющего оценить параметры линейных уравнений регрессии. В качестве одного из способов линеаризации используется логарифмирование уравнения. Рассмотрим процедуру линеаризации для каждого из предложенных вариантов ответа. Уравнение  ; проведем логарифмирование уравнения, тогда модель примет линейный вид
; проведем логарифмирование уравнения, тогда модель примет линейный вид  . Уравнение
. Уравнение 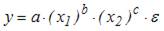 ; проведем логарифмирование уравнения, тогда модель примет линейный вид
; проведем логарифмирование уравнения, тогда модель примет линейный вид  . Уравнение
. Уравнение  ; проведем логарифмирование уравнения, тогда модель примет линейный вид
; проведем логарифмирование уравнения, тогда модель примет линейный вид  . Уравнение
. Уравнение  ; проведем замену переменных: пусть
; проведем замену переменных: пусть  , тогда модель примет линейный вид, то есть данное уравнение линеаризовано не с использованием способа логарифмирования уравнения. Уравнение
, тогда модель примет линейный вид, то есть данное уравнение линеаризовано не с использованием способа логарифмирования уравнения. Уравнение  является правильным вариантом ответа, так как другие регрессионные модели были линеаризованы путем логарифмирования уравнения.
является правильным вариантом ответа, так как другие регрессионные модели были линеаризованы путем логарифмирования уравнения.
 ЗАДАНИЕ N 14 сообщить об ошибке
ЗАДАНИЕ N 14 сообщить об ошибке
Тема: Нелинейные зависимости в экономике
Уравнением нелинейной регрессии, отражающей полиномиальную зависимость y от x, является …
Решение:
Одним из видов нелинейных зависимостей в эконометрике являются полиномиальные зависимости в виде функции  , где k – степень полинома. Так, полином первой степени имеет вид
, где k – степень полинома. Так, полином первой степени имеет вид  (линейная функция – частный вид полинома первой степени), полином второй степени –
(линейная функция – частный вид полинома первой степени), полином второй степени –  , третьей степени –
, третьей степени –  и т.д. до полинома степени k. Из предложенных вариантов ответа полиномом является модель вида
и т.д. до полинома степени k. Из предложенных вариантов ответа полиномом является модель вида  (это правильный вариант ответа). Рассмотрим другие варианты:
(это правильный вариант ответа). Рассмотрим другие варианты:  – линейное уравнение множественной регрессии;
– линейное уравнение множественной регрессии;  и
и 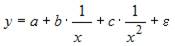 – нелинейные уравнения парной регрессии, отражающие гиперболическую зависимость. Эти три нелинейных зависимости не являются полиномами.
– нелинейные уравнения парной регрессии, отражающие гиперболическую зависимость. Эти три нелинейных зависимости не являются полиномами.
 ЗАДАНИЕ N 15 сообщить об ошибке
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Оценка качества нелинейных уравнений регрессии
По 20 регионам страны изучалась зависимость уровня безработицы y (%) от индекса потребительских цен x (% к предыдущему году) и построено уравнение в логарифмах исходных показателей:  . Коэффициент корреляции между логарифмами исходных показателей составил
. Коэффициент корреляции между логарифмами исходных показателей составил  . Коэффициент детерминации для модели в исходных показателях равен …
. Коэффициент детерминации для модели в исходных показателях равен …
Решение:
Коэффициент детерминации для модели в исходных показателях в данном случае будет равен коэффициенту детерминации для модели в логарифмах исходных показателей, который вычисляется как квадрат коэффициента корреляции, то есть 0,64.
Бывшев В.А. Эконометрика: учеб. пособие / В.А. Бывшев. – М.: Финансы и статистика, 2008. – С.331–346.
 ЗАДАНИЕ N 16 сообщить об ошибке
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Виды нелинейных уравнений регрессии
Уравнением нелинейной регрессии, линейной по параметрам является …
Решение:
Рассмотрим каждую из моделей. Уравнение  является нелинейным как по параметрам, так и по переменным. Уравнение
является нелинейным как по параметрам, так и по переменным. Уравнение  является нелинейным по переменной х, но линейным по параметрам. Уравнения
является нелинейным по переменной х, но линейным по параметрам. Уравнения  и
и 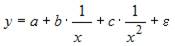 также являются нелинейными по переменной х, но линейными по параметрам. Поэтому правильный вариант ответа – «
также являются нелинейными по переменной х, но линейными по параметрам. Поэтому правильный вариант ответа – «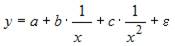 ». Другие модели не удовлетворяют поставленному условию.
». Другие модели не удовлетворяют поставленному условию.
 ЗАДАНИЕ N 17 сообщить об ошибке
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Свойства оценок параметров эконометрической модели, получаемых при помощи МНК
Для регрессионной модели состоятельность оценки параметра означает, что при увеличении выборки значение оценки параметра стремиться к …

|
|
| истинному значению параметра, вычисленному для генеральной совокупности
|
|
|
|
| оцениваемому параметру, рассчитанному по другой выборке, объем которой значительно меньше исходной совокупности данных
|
|
|
|
| свободному члену уравнения регрессии
|
|
|
|
| коэффициенту парной корреляции между зависимой переменной и соответствующей независимой переменной
|
Решение:
Желательными свойствами оценок параметров регрессионной модели являются состоятельность, несмещенность и эффективность. Понятие состоятельности оценки формулируется следующим образом: «Оценка  параметра
параметра  называется состоятельной, если значение оценки параметра сходится по вероятности к значению параметра генеральной совокупности при условии, что объем выборки стремится к бесконечности». Поэтому верным ответом является «истинному значению параметра, вычисленному для генеральной совокупности».
называется состоятельной, если значение оценки параметра сходится по вероятности к значению параметра генеральной совокупности при условии, что объем выборки стремится к бесконечности». Поэтому верным ответом является «истинному значению параметра, вычисленному для генеральной совокупности».
 ЗАДАНИЕ N 18 сообщить об ошибке
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Оценка параметров линейных уравнений регрессии
Метод наименьших квадратов (МНК) может применяться для оценки параметров исходной регрессионной модели в _________ форме.

|
|
| линейной
|
|
|
|
| нелинейной
|
|
|
|
| экспоненциальной
|
|
|
|
| нормальной
|
Решение:
Одним из типов эконометрических моделей является уравнение регрессии, которое может быть записано в виде математического выражения  , где y – зависимая переменная, xj – независимая переменная (j = 1,…, k; k – количество независимых переменных), f – тип функциональной зависимости (математическая функция),
, где y – зависимая переменная, xj – независимая переменная (j = 1,…, k; k – количество независимых переменных), f – тип функциональной зависимости (математическая функция),  – случайные факторы.
– случайные факторы.
Метод наименьших квадратов (МНК) применяется для оценки параметров линейных регрессионных моделей (f – линейная математическая функция). Поэтому правильный вариант ответа – «в линейной форме». При применении МНК к нелинейным уравнениям, в том числе и к экспоненциальным, исходную модель линеаризуют и МНК применяют к линеаризованной модели, к исходной нелинейной модели МНК не применяют. Поэтому варианты ответов – «в нелинейной форме» и в «экспоненциальной форме» неверные. При применении МНК оценки параметров находят на основе системы нормальных уравнений, в которой неизвестными величинами являются искомые значения оценок параметров, но исходная модель должна являться линейной. Вариант ответа «в нормальной форме» не является правильным, а только может ассоциироваться с понятием «система нормальных уравнений МНК».
 ЗАДАНИЕ N 19 сообщить об ошибке
ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Предпосылки МНК, методы их проверки
Значение критерия Дарбина – Уотсона можно приблизительно рассчитать по формуле  , где
, где 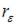 – значение коэффициента автокорреляции остатков модели. Максимальная величина значения
– значение коэффициента автокорреляции остатков модели. Максимальная величина значения  будет наблюдаться при ________ автокорреляции остатков.
будет наблюдаться при ________ автокорреляции остатков.

|
|
| отрицательной
|
|
|
|
| положительной
|
|
|
|
| нулевой
|
|
|
|
| бесконечно малой
|
Решение:
Значение коэффициента автокорреляции остатков модели  рассчитывается по аналогии с парным коэффициентом автокорреляции и изменяется в таких же пределах, то есть от –1 до +1. Подставим эти граничные значения в формулу для расчета значения критерия Дарбина – Уотсона: если
рассчитывается по аналогии с парным коэффициентом автокорреляции и изменяется в таких же пределах, то есть от –1 до +1. Подставим эти граничные значения в формулу для расчета значения критерия Дарбина – Уотсона: если  , то
, то  ; если
; если  , то
, то  . Поэтому значение
. Поэтому значение  меняется от 0 до 4. Максимальное значение
меняется от 0 до 4. Максимальное значение  равно 4 для случая, когда
равно 4 для случая, когда  , то есть для отрицательной автокорреляции остатков.
, то есть для отрицательной автокорреляции остатков.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 436 – 442.
Бывшев, В.А. Эконометрика: учеб. пособие / В.А. Бывшев. – М.: Финансы и статистика, 2008 – С 189 – 194.
 ЗАДАНИЕ N 20 сообщить об ошибке
ЗАДАНИЕ N 20 сообщить об ошибке
Тема: Обобщенный метод наименьших квадратов (ОМНК)
Проводится оценка параметров линейной модели парной регрессии  . Было выявлено, что остатки модели
. Было выявлено, что остатки модели  являются гетероскедастичными и дисперсия остатков
являются гетероскедастичными и дисперсия остатков  пропорциональна величине
пропорциональна величине  (
( , где
, где  – постоянная дисперсия). Оценку параметров предложено провести с помощью обобщенного метода наименьших квадратов, тогда преобразование исходных переменных модели
– постоянная дисперсия). Оценку параметров предложено провести с помощью обобщенного метода наименьших квадратов, тогда преобразование исходных переменных модели  будет иметь вид …
будет иметь вид …
Решение:
Метод наименьших квадратов (МНК) позволяет рассчитать такие оценки параметров линейной модели регрессии, для которых сумма квадратов отклонений фактических значений зависимой переменной y от ее модельных (теоретических) значений  минимальна. Отклонение
минимальна. Отклонение  , посчитанное для i -го наблюдения является ошибкой модели. При применении МНК относительно остатков регрессионной модели выдвигаются определенные предпосылки. Если остатки не удовлетворяют предпосылкам МНК, то применение обычного (традиционного) МНК нецелесообразно. Остатки гетероскедастичны (предпосылка нарушена), поэтому расчет оценок параметров проводят с использованием обобщенного метода наименьших квадратов (ОМНК) на основе преобразования переменных. Так как дисперсия остатков
, посчитанное для i -го наблюдения является ошибкой модели. При применении МНК относительно остатков регрессионной модели выдвигаются определенные предпосылки. Если остатки не удовлетворяют предпосылкам МНК, то применение обычного (традиционного) МНК нецелесообразно. Остатки гетероскедастичны (предпосылка нарушена), поэтому расчет оценок параметров проводят с использованием обобщенного метода наименьших квадратов (ОМНК) на основе преобразования переменных. Так как дисперсия остатков  пропорциональна величине
пропорциональна величине  :
:  , то модель примет вид
, то модель примет вид  . Разделим все выражение на величину
. Разделим все выражение на величину  , получаем
, получаем  . Таким образом, получены новые переменные модели
. Таким образом, получены новые переменные модели  , что и является верным вариантом ответа. Остальные варианты – неверные, так как они не были получены на этапе преобразования.
, что и является верным вариантом ответа. Остальные варианты – неверные, так как они не были получены на этапе преобразования.
Эконометрика: учеб. / И.И. Елисеева [и др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 201-203.
 ЗАДАНИЕ N 21 сообщить об ошибке
ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Общие понятия о системах уравнений, используемых в эконометрике
Система эконометрических уравнений не может состоять из …

|
|
| одного уравнения регрессии
|

|
|
| совокупности неравенств
|
|
|
|
| трех уравнений регрессии
|
|
|
|
| пяти уравнений регрессии
|
 ЗАДАНИЕ N 22 сообщить об ошибке
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Идентификация систем эконометрических уравнений
Дана структурная форма модели системы одновременных уравнений: 
Установите соответствие между обозначением и его наименованием:
(1) 
(2) 
(3) 
|
|
|
| структурный коэффициент
|
|
|
|
| ошибка уравнения системы
|
|
|
|
| эндогенная переменная
|
|
|
|
| приведенный коэффициент
|
Решение:
Рассмотрим каждое из обозначений.
(1) –  – структурный коэффициент или коэффициент структурной формы модели, которая отражает структуру связей между переменными.
– структурный коэффициент или коэффициент структурной формы модели, которая отражает структуру связей между переменными.
(2) –  – ошибка уравнения системы.
– ошибка уравнения системы.
(3) –  – зависимая переменная, то есть эндогенная переменная системы.
– зависимая переменная, то есть эндогенная переменная системы.
Вариант ответа «приведенный коэффициент» не является наименованием ни одного из обозначений (это неправильный вариант ответа); кроме этого, приведенные коэффициенты содержатся в приведенной форме модели, а в постановке задания приведена структурная форма модели.
 ЗАДАНИЕ N 23 сообщить об ошибке
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Методы оценки параметров систем одновременных уравнений: косвенный метод наименьших квадратов (КМНК) и двухшаговый метод наименьших квадратов (ДМНК)
Если записать типы эконометрических моделей в следующем порядке:
1) точно идентифицируемая система одновременных уравнений,
2) сверхидентифицируемая система одновременных уравнений,
3) уравнение множественной регрессии,
4) уравнение множественной регрессии при автокорреляции остатков,
то методы, применяемые для нахождения параметров соответствующих типов эконометрических моделей, будут расположены в следующем порядке
|
|
|
| косвенный метод наименьших квадратов
|
|
|
|
| двухшаговый метод наименьших квадратов
|
|
|
|
| метод наименьших квадратов
|
|
|
|
| обобщенный метод наименьших квадратов
|
Решение:
Для нахождения структурных коэффициентов точно идентифицируемой системы одновременных уравнений применяется косвенный метод наименьших квадратов.
Для нахождения структурных коэффициентов сверхидентифицируемой системы одновременных уравнений применяется двухшаговый метод наименьших квадратов.
Для нахождения параметров уравнения множественной регрессии применяется обычный метод наименьших квадратов.
Для нахождения параметров уравнения множественной регрессии при наличии гетероскедатичности или автокорреляции остатков применяется обобщенный метод наименьших квадратов.
Поэтому порядок методов, соответствующих типам эконометрических моделей будет следующий:
– косвенный метод наименьших квадратов;
– двухшаговый метод наименьших квадратов;
– метод наименьших квадратов;
– обобщенный метод наименьших квадратов.
Магнус, Ян Р. Эконометрика: нач. курс: [учеб. для студентов вузов по экон. специальностям] / Я. Р. Магнус, П. К. Катышев, А. А. Пересецкий; Акад. нар. хоз-ва при Правительстве РФ. – М.: Дело, 2005. – С.197–215.
Кремер, Н.Ш. Эконометрика: учеб. для студентов вузов / Н. Ш. Кремер, Б. А. П


 ЗАДАНИЕ N 2 сообщить об ошибке
ЗАДАНИЕ N 2 сообщить об ошибке – среднее и
– среднее и 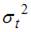 – дисперсия. Если временной ряд является стационарным, то …
– дисперсия. Если временной ряд является стационарным, то …


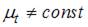

 количество оцениваемых параметров равно …
количество оцениваемых параметров равно … ,
, ,
, 
 для типа дома кирпичный
для типа дома кирпичный
 для типа дома монолитный
для типа дома монолитный
 для типа дома кирпичный
для типа дома кирпичный
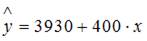 для типа дома монолитный
для типа дома монолитный
 ,
,  . Уравнение примет вид:
. Уравнение примет вид:  или
или  ,
,  . Уравнение примет вид
. Уравнение примет вид 
 . Величина коэффициента регрессии при переменной х2 свидетельствует о том, что при изменении уровня безработицы на 1% среднедушевой денежный доход ______ рубля при неизменной величине валового регионального продукта.
. Величина коэффициента регрессии при переменной х2 свидетельствует о том, что при изменении уровня безработицы на 1% среднедушевой денежный доход ______ рубля при неизменной величине валового регионального продукта. (y – зависимая переменная; х(j) – независимая переменная; j = 1,…, k; k – количество независимых переменных). При проверке независимых переменных на отсутствие мультиколлинеарности должно выполняться требование: для любых j и l
(y – зависимая переменная; х(j) – независимая переменная; j = 1,…, k; k – количество независимых переменных). При проверке независимых переменных на отсутствие мультиколлинеарности должно выполняться требование: для любых j и l  абсолютное значение парного коэффициента линейной корреляции
абсолютное значение парного коэффициента линейной корреляции  …
… 0
0
 в скобках указаны значения t -статистики соответствующие параметрам регрессии. Также известны критические значения Стьюдента для 10 степеней свободы для различных уровней значимости
в скобках указаны значения t -статистики соответствующие параметрам регрессии. Также известны критические значения Стьюдента для 10 степеней свободы для различных уровней значимости  ,
,  ,
, 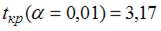 . Для данного уравнения при уровне значимости α=0,05 значимыми являются параметры …
. Для данного уравнения при уровне значимости α=0,05 значимыми являются параметры …



 формулируется нулевая гипотеза
формулируется нулевая гипотеза 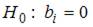 при альтернативной гипотезе
при альтернативной гипотезе  . Затем рассчитывается фактическое значение t -статистики, которое сравнивается с критическим значением Стьюдента
. Затем рассчитывается фактическое значение t -статистики, которое сравнивается с критическим значением Стьюдента  для требуемого числа степеней свободы и уровня значимости. Если
для требуемого числа степеней свободы и уровня значимости. Если  , коэффициент
, коэффициент  , коэффициент
, коэффициент  , где
, где 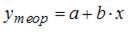 рассчитаны дисперсии:
рассчитаны дисперсии:  ;
;  ;
; 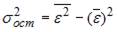 . Тогда величина коэффициента детерминации рассчитывается по формуле …
. Тогда величина коэффициента детерминации рассчитывается по формуле …
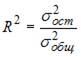


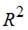 характеризует долю дисперсии зависимой переменной, объясненную построенным уравнением регрессии, в общей дисперсии зависимой переменной, то есть
характеризует долю дисперсии зависимой переменной, объясненную построенным уравнением регрессии, в общей дисперсии зависимой переменной, то есть  .
. показателем тесноты связи является …
показателем тесноты связи является … . Верный вариант – «коэффициент множественной корреляции». Вариант «парный коэффициент корреляции» неверный, так как в данном случае рассматривается уравнение множественной регрессии. Вариант «коэффициент автокорреляции» неверный, так как автокорреляция предполагает исследование тесноты связи внутри одного ряда. Вариант «F-критерий Фишера» неверный, так как данный показатель используется для оценки существенности связи и значимости построенного уравнения, но не для оценки тесноты связи.
. Верный вариант – «коэффициент множественной корреляции». Вариант «парный коэффициент корреляции» неверный, так как в данном случае рассматривается уравнение множественной регрессии. Вариант «коэффициент автокорреляции» неверный, так как автокорреляция предполагает исследование тесноты связи внутри одного ряда. Вариант «F-критерий Фишера» неверный, так как данный показатель используется для оценки существенности связи и значимости построенного уравнения, но не для оценки тесноты связи.
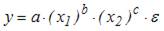


 . Уравнение
. Уравнение  . Уравнение
. Уравнение  . Уравнение
. Уравнение  , тогда модель примет линейный вид, то есть данное уравнение линеаризовано не с использованием способа логарифмирования уравнения. Уравнение
, тогда модель примет линейный вид, то есть данное уравнение линеаризовано не с использованием способа логарифмирования уравнения. Уравнение 

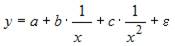
 , где k – степень полинома. Так, полином первой степени имеет вид
, где k – степень полинома. Так, полином первой степени имеет вид  (линейная функция – частный вид полинома первой степени), полином второй степени –
(линейная функция – частный вид полинома первой степени), полином второй степени –  , третьей степени –
, третьей степени –  и т.д. до полинома степени k. Из предложенных вариантов ответа полиномом является модель вида
и т.д. до полинома степени k. Из предложенных вариантов ответа полиномом является модель вида  . Коэффициент корреляции между логарифмами исходных показателей составил
. Коэффициент корреляции между логарифмами исходных показателей составил  . Коэффициент детерминации для модели в исходных показателях равен …
. Коэффициент детерминации для модели в исходных показателях равен …





 параметра
параметра  называется состоятельной, если значение оценки параметра сходится по вероятности к значению параметра генеральной совокупности при условии, что объем выборки стремится к бесконечности». Поэтому верным ответом является «истинному значению параметра, вычисленному для генеральной совокупности».
называется состоятельной, если значение оценки параметра сходится по вероятности к значению параметра генеральной совокупности при условии, что объем выборки стремится к бесконечности». Поэтому верным ответом является «истинному значению параметра, вычисленному для генеральной совокупности». , где y – зависимая переменная, xj – независимая переменная (j = 1,…, k; k – количество независимых переменных), f – тип функциональной зависимости (математическая функция),
, где y – зависимая переменная, xj – независимая переменная (j = 1,…, k; k – количество независимых переменных), f – тип функциональной зависимости (математическая функция),  – случайные факторы.
– случайные факторы. , где
, где 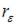 – значение коэффициента автокорреляции остатков модели. Максимальная величина значения
– значение коэффициента автокорреляции остатков модели. Максимальная величина значения  будет наблюдаться при ________ автокорреляции остатков.
будет наблюдаться при ________ автокорреляции остатков. рассчитывается по аналогии с парным коэффициентом автокорреляции и изменяется в таких же пределах, то есть от –1 до +1. Подставим эти граничные значения в формулу для расчета значения критерия Дарбина – Уотсона: если
рассчитывается по аналогии с парным коэффициентом автокорреляции и изменяется в таких же пределах, то есть от –1 до +1. Подставим эти граничные значения в формулу для расчета значения критерия Дарбина – Уотсона: если  , то
, то  ; если
; если  , то
, то  . Поэтому значение
. Поэтому значение  меняется от 0 до 4. Максимальное значение
меняется от 0 до 4. Максимальное значение  , то есть для отрицательной автокорреляции остатков.
, то есть для отрицательной автокорреляции остатков. . Было выявлено, что остатки модели
. Было выявлено, что остатки модели  являются гетероскедастичными и дисперсия остатков
являются гетероскедастичными и дисперсия остатков  пропорциональна величине
пропорциональна величине  (
( , где
, где  – постоянная дисперсия). Оценку параметров предложено провести с помощью обобщенного метода наименьших квадратов, тогда преобразование исходных переменных модели
– постоянная дисперсия). Оценку параметров предложено провести с помощью обобщенного метода наименьших квадратов, тогда преобразование исходных переменных модели  будет иметь вид …
будет иметь вид …
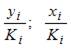


 минимальна. Отклонение
минимальна. Отклонение  , посчитанное для i -го наблюдения является ошибкой модели. При применении МНК относительно остатков регрессионной модели выдвигаются определенные предпосылки. Если остатки не удовлетворяют предпосылкам МНК, то применение обычного (традиционного) МНК нецелесообразно. Остатки гетероскедастичны (предпосылка нарушена), поэтому расчет оценок параметров проводят с использованием обобщенного метода наименьших квадратов (ОМНК) на основе преобразования переменных. Так как дисперсия остатков
, посчитанное для i -го наблюдения является ошибкой модели. При применении МНК относительно остатков регрессионной модели выдвигаются определенные предпосылки. Если остатки не удовлетворяют предпосылкам МНК, то применение обычного (традиционного) МНК нецелесообразно. Остатки гетероскедастичны (предпосылка нарушена), поэтому расчет оценок параметров проводят с использованием обобщенного метода наименьших квадратов (ОМНК) на основе преобразования переменных. Так как дисперсия остатков  . Разделим все выражение на величину
. Разделим все выражение на величину  , получаем
, получаем  . Таким образом, получены новые переменные модели
. Таким образом, получены новые переменные модели  , что и является верным вариантом ответа. Остальные варианты – неверные, так как они не были получены на этапе преобразования.
, что и является верным вариантом ответа. Остальные варианты – неверные, так как они не были получены на этапе преобразования.






