Известно, что доля объясненной дисперсии в общей дисперсии равна 0,2. Тогда значение коэффициента детерминации составляет …
Решение:
Коэффициент детерминации 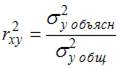 равен доле дисперсии, объясненной регрессией, в общей дисперсии. Следовательно,
равен доле дисперсии, объясненной регрессией, в общей дисперсии. Следовательно, 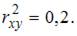
Эконометрика. Краткий курс: учеб. пособие / С.А. Айвазян, С.С. Иванова. – М.: Маркет ДС, 2007. – С.59–61.
 ЗАДАНИЕ N 2 сообщить об ошибке
ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Предпосылки МНК, методы их проверки
Одной из предпосылок метода наименьших квадратов является то, что величина  , равная среднему значению отклонений фактических значений зависимой переменной y от ее модельных (теоретических) значений
, равная среднему значению отклонений фактических значений зависимой переменной y от ее модельных (теоретических) значений  , должна быть равна …
, должна быть равна …
Решение:
Метод наименьших квадратов МНК позволяет рассчитать такие оценки параметров линейной модели регрессии, для которых сумма квадратов отклонений фактических значений зависимой переменной y от ее модельных (теоретических) значений  минимальна. Отклонение
минимальна. Отклонение  является ошибкой модели. Так, если модель регрессии записана в виде выражения
является ошибкой модели. Так, если модель регрессии записана в виде выражения 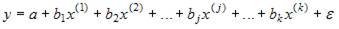 , где
, где  , то разность
, то разность  (
( – ошибка модели).
– ошибка модели).
При применении МНК величина  должна удовлетворять определенным условиям (предпосылкам). Предпосылкой метода наименьших квадратов МНК является
должна удовлетворять определенным условиям (предпосылкам). Предпосылкой метода наименьших квадратов МНК является  , т.е. «величина
, т.е. «величина  , равная среднему значению отклонений фактических значений зависимой переменной y от ее модельных (теоретических) значений
, равная среднему значению отклонений фактических значений зависимой переменной y от ее модельных (теоретических) значений  , должна быть равна 0». Верным ответом является «0». Остальные варианты ответов – неверные.
, должна быть равна 0». Верным ответом является «0». Остальные варианты ответов – неверные.
 ЗАДАНИЕ N 3 сообщить об ошибке
ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Обобщенный метод наименьших квадратов (ОМНК)
Обобщенный метод наименьших квадратов не может применяться для оценки параметров линейных регрессионных моделей в случае, если …

|
|
| средняя величина остатков не равна нулю
|
|
|
|
| остатки гетероскедастичны
|
|
|
|
| остатки автокоррелированны
|
|
|
|
| дисперсия остатков не является постоянной величиной
|
Решение:
Метод наименьших квадратов (МНК) позволяет рассчитать такие оценки параметров линейной модели регрессии, для которых сумма квадратов отклонений фактических значений зависимой переменной y от ее модельных (теоретических) значений  минимальна. Отклонение
минимальна. Отклонение  , посчитанное для i -го наблюдения, является ошибкой модели. Предпосылками МНК являются: случайный характер остатков, нулевая средняя величина, отсутствие автокорреляции в остатках, постоянная дисперсия (гомоскедастичность) остатков, подчинение нормальному закону распределения. Если остатки автокоррелированны и/или гетероскедастичны, то проводят преобразование переменных и расчет оценок параметров осуществляют с использованием обобщенного метода наименьших квадратов (ОМНК). При этом такая предпосылка как нулевая средняя величина остатков сохраняется. Поэтому обобщенный метод наименьших квадратов не может применяться, если средняя величина остатков не равна нулю.
, посчитанное для i -го наблюдения, является ошибкой модели. Предпосылками МНК являются: случайный характер остатков, нулевая средняя величина, отсутствие автокорреляции в остатках, постоянная дисперсия (гомоскедастичность) остатков, подчинение нормальному закону распределения. Если остатки автокоррелированны и/или гетероскедастичны, то проводят преобразование переменных и расчет оценок параметров осуществляют с использованием обобщенного метода наименьших квадратов (ОМНК). При этом такая предпосылка как нулевая средняя величина остатков сохраняется. Поэтому обобщенный метод наименьших квадратов не может применяться, если средняя величина остатков не равна нулю.
Эконометрика: учеб. / под ред. И.И. Елисеевой. – М.: Проспект, 2009. – С. 82–89.
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С. 93–112.
Магнус, Ян Р. Эконометрика: начальный курс: Учебник для студ-ов вузов, обуч. по экон. спец. / Я.Р. Магнус, П.К. Катышев, А.А. Пересецкий; Акад. народ. хоз-ва при Правительстве Рос. Федерации. – М.: Дело, 2000. – С. 130–135.
 ЗАДАНИЕ N 4 сообщить об ошибке
ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Свойства оценок параметров эконометрической модели, получаемых при помощи МНК
Пусть  – оценка параметра
– оценка параметра  регрессионной модели, полученная с помощью метода наименьших квадратов;
регрессионной модели, полученная с помощью метода наименьших квадратов; 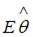 – математическое ожидание оценки
– математическое ожидание оценки  . В том случае если
. В том случае если 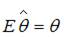 , то оценка обладает свойством …
, то оценка обладает свойством …

|
|
| несмещенности
|
|
|
|
| состоятельности
|
|
|
|
| эффективности
|
|
|
|
| смещенности
|
 ЗАДАНИЕ N 5 сообщить об ошибке
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Виды нелинейных уравнений регрессии
Уравнением нелинейной регрессии, являющейся нелинейной по параметрам является …
Решение:
Рассмотрим каждую из моделей. Уравнение  является нелинейным как по параметрам, так и по переменным. Уравнение
является нелинейным как по параметрам, так и по переменным. Уравнение  является нелинейным по переменной х, но линейным по параметрам. Уравнения
является нелинейным по переменной х, но линейным по параметрам. Уравнения  и
и 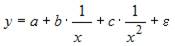 также являются нелинейными по переменной х, но линейными по параметрам. Поэтому правильный вариант ответа – «
также являются нелинейными по переменной х, но линейными по параметрам. Поэтому правильный вариант ответа – « ». Другие модели не удовлетворяют поставленному условию.
». Другие модели не удовлетворяют поставленному условию.
 ЗАДАНИЕ N 6 сообщить об ошибке
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Линеаризация нелинейных моделей регрессии
При линеаризации нелинейных регрессионных моделей как один из видов преобразований используется способ приведения уравнения к обратному виду, то есть к переменной  . Указанным способом может быть линеаризовано уравнение …
. Указанным способом может быть линеаризовано уравнение …
Решение:
Линеаризация – это процедура приведения нелинейной регрессионной модели к линейному виду путем различных математических преобразований. Это необходимо для обеспечения возможности использования метода наименьших квадратов, позволяющего оценить параметры линейных уравнений регрессии. В качестве одного из способов линеаризации используется метод приведения уравнения к обратному виду, то есть к переменной  . Рассмотрим процедуру линеаризации для каждого из предложенных вариантов ответа. Уравнение
. Рассмотрим процедуру линеаризации для каждого из предложенных вариантов ответа. Уравнение  ; проведем замену переменных: пусть
; проведем замену переменных: пусть  , тогда модель примет линейный вид
, тогда модель примет линейный вид  . Уравнение
. Уравнение  ; проведем логарифмирование уравнения, тогда модель примет линейный вид
; проведем логарифмирование уравнения, тогда модель примет линейный вид  . Уравнение
. Уравнение  ; проведем логарифмирование уравнения, тогда модель примет линейный вид
; проведем логарифмирование уравнения, тогда модель примет линейный вид  . Уравнение
. Уравнение 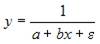 ; обратим уравнение, тогда модель примет линейный вид
; обратим уравнение, тогда модель примет линейный вид  . то есть данное уравнение линеаризовано с использованием способа приведения уравнения к обратному виду, или к переменной
. то есть данное уравнение линеаризовано с использованием способа приведения уравнения к обратному виду, или к переменной  . Уравнение
. Уравнение 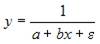 является правильным вариантом ответа, так как линеаризовано указанным в постановке вопроса способом. Другие модели линеаризованы не путем приведения уравнения к обратному виду.
является правильным вариантом ответа, так как линеаризовано указанным в постановке вопроса способом. Другие модели линеаризованы не путем приведения уравнения к обратному виду.
 ЗАДАНИЕ N 7 сообщить об ошибке
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Нелинейные зависимости в экономике
Если с увеличением масштабов производства удельный расход сырья сокращается, то моделирование целесообразно проводить на основе …

|
|
| равносторонней гиперболы
|
|
|
|
| степенной функции
|
|
|
|
| параболы второй степени
|
|
|
|
| экспоненциальной функции
|
Решение:
Равносторонняя гипербола обычно используется в эконометрике для характеристики связи удельных расходов сырья, материалов, топлива с объемом выпускаемой продукции, поскольку она позволяет учесть эффект масштаба, что с увеличением объемов выпускаемой продукции удельные показатели расходов сырья, материалов или топлива обычно падают.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 82.
Бывшев В.А. Эконометрика: учеб. пособие / В.А. Бывшев. – М.: Финансы и статистика, 2008. – С.331–346.
 ЗАДАНИЕ N 8 сообщить об ошибке
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Оценка качества нелинейных уравнений регрессии
Для нелинейной регрессионной модели зависимости рассчитано значение индекса детерминации R2 = 0,9. Тогда значение индекса корреляции составит …
 ЗАДАНИЕ N 9 сообщить об ошибке
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Временные ряды данных: характеристики и общие понятия
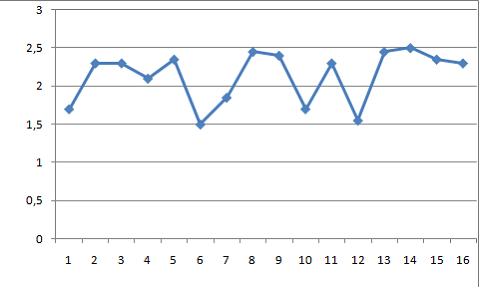
Ряд, уровни которого образуются как сумма среднего уровня ряда и некоторой случайной компоненты, изображен на графике …
Решение:
График ряда, уровни которого образуются как сумма среднего уровня ряда и некоторой случайной компоненты, будет колебаться относительно своего среднего значения.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 296–300.
Эконометрика: учеб. / под ред. Д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С.284–290.
 ЗАДАНИЕ N 10 сообщить об ошибке
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Модели стационарных и нестационарных временных рядов и их идентификация
Для стационарного временного ряда y1, у2, … yt, …, yn типа «белый шум» математическое ожидание E (yt) равно …
Решение:
Процесс «белый шум» является частным случаем стационарного временного ряда y1, у2, … yt, …, yn, для которого математическое ожидание значений уровня этого ряда равно 0, то есть E (yt) = 0 (где t = 1, …, n). Поэтому правильный вариант ответа – «0».
 ЗАДАНИЕ N 11 сообщить об ошибке
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Аддитивная и мультипликативная модели временных рядов
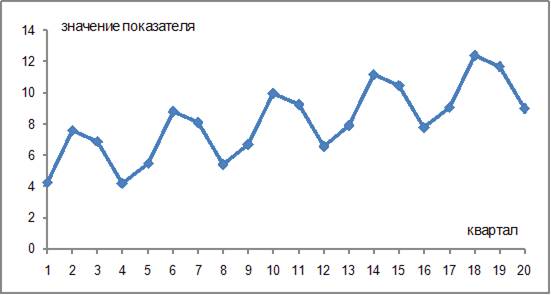
Для временного ряда, отображенного на рисунке одним из методов построения модели ряда является выравнивание ряда по методу скользящей средней. При этом количество слагаемых при расчете значений выровненного ряда будет равно …

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Уровень временного ряда (yt) формируется под воздействием различных факторов – компонент: Т (тенденция), S (циклические и/или сезонные колебания), Е (случайные факторы). При построении модели временного ряда основной задачей является выявление структуры исследуемого ряда (определение, из каких компонент состоит ряд) и вычисление значений компонент для каждого уровня ряда. Анализ структуры ряда (см. рис.) показал, что ряд содержит возрастающую тенденцию – компоненту Т; ряд также содержит сезонные колебания S, периодичность которых равна 4 кварталам. Одним из способов моделирования временного ряда при наличии S компоненты является сглаживание ряда, в этом случае число слагаемых при расчете скользящей средней равно периодичности временного ряда, то есть в нашем случае равно 4. Правильный ответ – «4».
 ЗАДАНИЕ N 12 сообщить об ошибке
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Структура временного ряда
Вывод о присутствии в данном временном ряде сезонной компоненты можно сделать по значению коэффициента автокорреляции ____ порядка.


|
|
| четвертого
|
|
|
|
| первого
|
|
|
|
| второго
|
|
|
|
| восьмого
|
Решение:
Структура временного ряда определяется по значениям коэффициента автокорреляции, рассчитанным для разных порядков коэффициента автокорреляции. Коэффициент автокорреляции характеризует тесноту связи между уровнями исходного ряда и уровнями этого же ряда, сдвинутыми на значение порядка. Если временной ряд содержит тенденцию, то наиболее высокое (максимальное или чуть меньше, чем максимальное) значение наблюдается у коэффициента автокорреляции первого порядка, так как оказываются тесно связанными два соседних уровня временного ряда. Если наблюдаются высокие значения для коэффициента автокорреляции более высоких порядков, то это свидетельствует о наличии во временном ряде периодических колебаний, период колебаний равен порядку соответствующего коэффициента автокорреляции. Так как в задании спрашивается о сезонных колебаниях, то необходимо по графику определить периодичность этих колебаний, в нашем случае она равна 4 кварталам. Поэтому правильный вариант ответа – «четвертого».
 ЗАДАНИЕ N 13 сообщить об ошибке
ЗАДАНИЕ N 13 сообщить об ошибке
Тема: Методы оценки параметров систем одновременных уравнений: косвенный метод наименьших квадратов (КМНК) и двухшаговый метод наименьших квадратов (ДМНК)
При проверке счетного правила выяснилось, что для всех уравнений системы одновременных уравнений выполняется необходимое условие идентификации и все уравнения по счетному правилу точно идентифицируемы. Чтобы получить структурные коэффициенты системы, действия нужно выполнить в следующем порядке:
|
|
|
| для каждого уравнения проверить условие неравенства нулю определителя матрицы коэффициентов, присутствующих в других уравнениях, но отсутствующих в данном уравнении
|
|
|
|
| преобразовать структурную форму модели в приведенную форму модели
|
|
|
|
| для каждого уравнения приведенной формы модели обычным методом наименьших квадратов оценить приведенные коэффициенты
|
|
|
|
| коэффициенты приведенной формы модели преобразовать в параметры структурной модели
|
 ЗАДАНИЕ N 14 сообщить об ошибке
ЗАДАНИЕ N 14 сообщить об ошибке
Тема: Идентификация систем эконометрических уравнений
Установите соответствие между видом системы одновременных (совместных) эконометрических уравнений и формой модели:
(1) 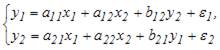
(2) 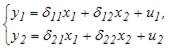
|
|
|
| структурная форма модели
|
|
|
|
| приведенная форма модели
|
|
|
|
| форма нормальных уравнений
|
Решение:
Рассмотрим каждую из систем эконометрических уравнений.
В системе (1) в правой части уравнений стоят как зависимые переменные y других уравнений, так и независимые переменные х. Такая форма модели отражает структуру связей между переменными и называется структурной формой модели.
В системе (2) в правой части уравнений стоят только независимые переменные с приведенными коэффициентами  , такая форма модели называется приведенной формой модели.
, такая форма модели называется приведенной формой модели.
Вариант «форма нормальных уравнений», предложенный в ответе, не является формой системы одновременных уравнений, это неправильный вариант ответа.
 ЗАДАНИЕ N 15 сообщить об ошибке
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Общие понятия о системах уравнений, используемых в эконометрике
Модель равенства спроса и предложения, где предложение  и спрос
и спрос  являются линейными функциями цены p, состоит из уравнений …
являются линейными функциями цены p, состоит из уравнений …
Решение:
В модели предложение  и спрос
и спрос  являются линейными функциями цены p. Значит, уравнение для предложения
являются линейными функциями цены p. Значит, уравнение для предложения  будет иметь вид
будет иметь вид  , а уравнение для спроса
, а уравнение для спроса  –
– 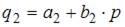 . Так как рассматривается модель равенства спроса и предложения, значит, первые два уравнения должны быть дополнены третьим:
. Так как рассматривается модель равенства спроса и предложения, значит, первые два уравнения должны быть дополнены третьим:  .
.
Модель будет иметь вид
 ,
,
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С.341–355.
 ЗАДАНИЕ N 16 сообщить об ошибке
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Классификация систем уравнений
Установите соответствие между видом и классом системы эконометрических уравнений:
(1) 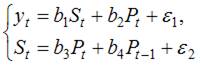
(2) 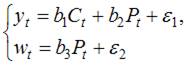
|
|
|
| система одновременных уравнений с лаговыми переменными
|
|
|
|
| система независимых уравнений
|
|
|
|
| система одновременных уравнений без лаговых переменных
|
Решение:
Рассмотрим каждую из систем эконометрических уравнений.
В системе (1) в правой части первого уравнения стоит переменная St, которая во втором уравнении находится в левой части, следовательно, система является системой одновременных уравнений. Во втором уравнении системы (1) одновременно с переменной Pt находится лаговая переменная Pt-1, поэтому система (1) является системой одновременных уравнений с лаговыми переменными.
В системе (2) в левой части представлены переменные yt и wt, которые не входят в правую часть уравнений системы, поэтому система (2) является системой независимых уравнений.
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С. 341–345.
Эконометрика: учеб. / под ред. И.И. Елисеевой. – М.: Проспект, 2009. – С. 230–233.
 ЗАДАНИЕ N 17 сообщить об ошибке
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Оценка значимости параметров эконометрической модели
В уравнения множественной регрессии, построенном на основании 14 наблюдений, 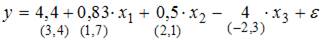 в скобках указаны значения t -статистики, соответствующие параметрам регрессии. Также известны критические значения Стьюдента для 10 степеней свободы для различных уровней значимости
в скобках указаны значения t -статистики, соответствующие параметрам регрессии. Также известны критические значения Стьюдента для 10 степеней свободы для различных уровней значимости  ,
,  ,
,  . При уровне значимости 0,1 значимыми являются параметры …
. При уровне значимости 0,1 значимыми являются параметры …
Решение:
Чтобы оценить значимость параметров регрессии используется t -критерий Стьюдента. Для каждого коэффициента регрессии  формулируется нулевая гипотеза
формулируется нулевая гипотеза 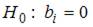 при альтернативной гипотезе
при альтернативной гипотезе  . Затем рассчитывается фактическое значение t -статистики, которое сравнивается с критическим значением Стьюдента
. Затем рассчитывается фактическое значение t -статистики, которое сравнивается с критическим значением Стьюдента  для требуемого числа степеней свободы и уровня значимости. Если
для требуемого числа степеней свободы и уровня значимости. Если  , коэффициент
, коэффициент  значим; если
значим; если  , коэффициент
, коэффициент  незначим. В нашем случае при уровне значимости 0,1 значимым является параметры
незначим. В нашем случае при уровне значимости 0,1 значимым является параметры  .
.
Эконометрика. Под ред. Елисеевой И.И., М.: Финансы и статистика, 2005. С.160–165.
Кремер, Н.Ш. Эконометрика: учеб. для студентов вузов / Н. Ш. Кремер, Б. А. Путко; ред. Н. Ш. Кремер. – М.: ЮНИТИ, 2002. – С.40–52.
 ЗАДАНИЕ N 18 сообщить об ошибке
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Проверка статистической значимости эконометрической модели
Для регрессионной модели известны следующие величины дисперсий:
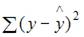 ;
;  ;
;  , где
, где 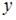 – значение зависимой переменной по исходным данным;
– значение зависимой переменной по исходным данным;  – значение зависимой переменной, вычисленное по регрессионной модели;
– значение зависимой переменной, вычисленное по регрессионной модели; 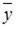 – среднее значение зависимой переменной, определенное по исходным статистическим данным. Для указанных дисперсий справедливо равенство …
– среднее значение зависимой переменной, определенное по исходным статистическим данным. Для указанных дисперсий справедливо равенство …
Решение:
Назовем приведенные дисперсии: 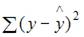 – общая дисперсия;
– общая дисперсия; 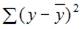 – объясненная дисперсия;
– объясненная дисперсия;  – остаточная дисперсия. При анализе статистической модели величину общей дисперсии рассматривают как сему объясненной и остаточной дисперсий, поэтому справедливо равенство:
– остаточная дисперсия. При анализе статистической модели величину общей дисперсии рассматривают как сему объясненной и остаточной дисперсий, поэтому справедливо равенство:  .
.
Эконометрика: учеб. / И. И. Елисеева [и др.]; под ред. И. И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 63-64.
 ЗАДАНИЕ N 19 сообщить об ошибке
ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Оценка тесноты связи
Значение коэффициента множественной корреляции рассчитывается по формуле  (
(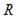 – коэффициент множественной корреляции;
– коэффициент множественной корреляции;  – коэффициент детерминации для уравнения множественной регрессии). Тогда значение коэффициента множественной корреляции
– коэффициент детерминации для уравнения множественной регрессии). Тогда значение коэффициента множественной корреляции 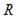 будет находится в интервале …
будет находится в интервале …

|
|
| [0; 1]
|
|
|
|
| [–1; 1]
|
|
|
|
| [–1; 0]
|
|
|
|
| [0;  ] ]
|
 ЗАДАНИЕ N 20 сообщить об ошибке
ЗАДАНИЕ N 20 сообщить об ошибке
Тема: Оценка качества подбора уравнения
Известно, что доля остаточной регрессии в общей составила 0,19. Тогда значение коэффициента корреляции равно …

|
|
| 0,9
|
|
|
|
| 0,19
|
|
|
|
| 0,81
|
|
|
|
| 0,95
|
Решение:
Известно, что доля остаточной регрессии в общей составила 0,19. Значит, 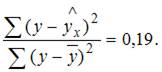 Найдем коэффициент детерминации:
Найдем коэффициент детерминации:  Вычислим коэффициент корреляции:
Вычислим коэффициент корреляции: 
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 137.
 ЗАДАНИЕ N 21 сообщить об ошибке
ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Линейное уравнение множественной регрессии
В эконометрической модели линейного уравнения регрессии 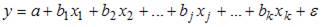 ошибкой модели является …
ошибкой модели является …

|
|
| 
|
|
|
|
| a
|
|
|
|
| bj
|
|
|
|
| xj
|
Решение:
Эконометрическая модель линейного уравнения регрессии имеет вид 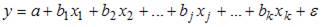 , где y – зависимая переменная, xj – независимая переменная (
, где y – зависимая переменная, xj – независимая переменная ( – номер независимой переменной в модели, k – общее количество независимых переменных в модели); a, bj – параметры уравнения;
– номер независимой переменной в модели, k – общее количество независимых переменных в модели); a, bj – параметры уравнения;  – ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Таким образом, верным ответом является «
– ошибка модели (учитывает влияние на зависимую переменную y прочих факторов, не являющихся в модели независимыми переменными). Таким образом, верным ответом является « ».
».
 ЗАДАНИЕ N 22 сообщить об ошибке
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Спецификация эконометрической модели
В модели вида 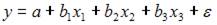 количество объясняющих переменных равно …
количество объясняющих переменных равно …
 ЗАДАНИЕ N 23 сообщить об ошибке
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Отбор факторов, включаемых в модель множественной регрессии
Для эконометрической модели линейного уравнения множественной регрессии вида  построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х(1), х(2), х(3) – независимые переменные):
построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х(1), х(2), х(3) – независимые переменные):

Количество пар коллинеарных независимых переменных в данной модели равно …

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
При построении модели множественной регрессии необходимо исключить возможность существования тесной линейной зависимости между объясняющими переменными, что ведет к проблеме мультиколлинеарности. При этом осуществляют проверку коэффициентов линейной корреляции для каждой пары объясняющих переменных. Эти значения отражены в матрице парных коэффициентов линейной корреляции. Считается, что наличие значений коэффициентов парной корреляции между объясняющими переменными, превышающих по абсолютной величине 0,7, отражает тесную связь между этими переменными. Такие объясняющие переменные называются коллинеарными. В матрице значения двух парных коэффициентов линейной корреляции по абсолютной величине превышают 0,7 ( ;
;  ). Верным вариантом ответа является «2». Другие варианты ответов являются неверными. Теснота связи с переменной y в данном случае не рассматривается, так как переменная y не является объясняющей переменной. Поэтому другие значения в матрице, превышающие 0,7, не отражают пары коллинеарных объясняющих переменных.
). Верным вариантом ответа является «2». Другие варианты ответов являются неверными. Теснота связи с переменной y в данном случае не рассматривается, так как переменная y не является объясняющей переменной. Поэтому другие значения в матрице, превышающие 0,7, не отражают пары коллинеарных объясняющих переменных.
 ЗАДАНИЕ N 24 сообщить об ошибке
ЗАДАНИЕ N 24 сообщить об ошибке
Тема: Фиктивные переменные
В эконометрике фиктивной переменной принято считать …

|
|
| переменную, принимающую значения 0 и 1
|

|
|
| описывающую количественным образом качественный признак
|
|
|
|
| переменную, которая может равняться только целому числу
|
|
|
|
| несущественную переменную
|
Решение:
Качественное различие признаков можно формализовать с помощью любой переменной, принимающей два значения, не обязательно 0 или 1. Однако в эконометрической практике почти всегда используются фиктивные переменные типа «0-1», поскольку в этом случае можно интерпретировать результаты моделирования.





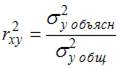 равен доле дисперсии, объясненной регрессией, в общей дисперсии. Следовательно,
равен доле дисперсии, объясненной регрессией, в общей дисперсии. Следовательно, 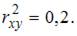
 ЗАДАНИЕ N 2 сообщить об ошибке
ЗАДАНИЕ N 2 сообщить об ошибке , равная среднему значению отклонений фактических значений зависимой переменной y от ее модельных (теоретических) значений
, равная среднему значению отклонений фактических значений зависимой переменной y от ее модельных (теоретических) значений  , должна быть равна …
, должна быть равна …

 является ошибкой модели. Так, если модель регрессии записана в виде выражения
является ошибкой модели. Так, если модель регрессии записана в виде выражения 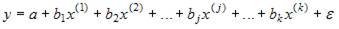 , где
, где  , то разность
, то разность  (
( – ошибка модели).
– ошибка модели).  должна удовлетворять определенным условиям (предпосылкам). Предпосылкой метода наименьших квадратов МНК является
должна удовлетворять определенным условиям (предпосылкам). Предпосылкой метода наименьших квадратов МНК является  , т.е. «величина
, т.е. «величина  минимальна. Отклонение
минимальна. Отклонение  , посчитанное для i -го наблюдения, является ошибкой модели. Предпосылками МНК являются: случайный характер остатков, нулевая средняя величина, отсутствие автокорреляции в остатках, постоянная дисперсия (гомоскедастичность) остатков, подчинение нормальному закону распределения. Если остатки автокоррелированны и/или гетероскедастичны, то проводят преобразование переменных и расчет оценок параметров осуществляют с использованием обобщенного метода наименьших квадратов (ОМНК). При этом такая предпосылка как нулевая средняя величина остатков сохраняется. Поэтому обобщенный метод наименьших квадратов не может применяться, если средняя величина остатков не равна нулю.
, посчитанное для i -го наблюдения, является ошибкой модели. Предпосылками МНК являются: случайный характер остатков, нулевая средняя величина, отсутствие автокорреляции в остатках, постоянная дисперсия (гомоскедастичность) остатков, подчинение нормальному закону распределения. Если остатки автокоррелированны и/или гетероскедастичны, то проводят преобразование переменных и расчет оценок параметров осуществляют с использованием обобщенного метода наименьших квадратов (ОМНК). При этом такая предпосылка как нулевая средняя величина остатков сохраняется. Поэтому обобщенный метод наименьших квадратов не может применяться, если средняя величина остатков не равна нулю. – оценка параметра
– оценка параметра  регрессионной модели, полученная с помощью метода наименьших квадратов;
регрессионной модели, полученная с помощью метода наименьших квадратов; 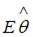 – математическое ожидание оценки
– математическое ожидание оценки 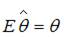 , то оценка обладает свойством …
, то оценка обладает свойством …


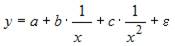
 . Указанным способом может быть линеаризовано уравнение …
. Указанным способом может быть линеаризовано уравнение …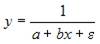


 , тогда модель примет линейный вид
, тогда модель примет линейный вид  . Уравнение
. Уравнение  . Уравнение
. Уравнение  . Уравнение
. Уравнение  . то есть данное уравнение линеаризовано с использованием способа приведения уравнения к обратному виду, или к переменной
. то есть данное уравнение линеаризовано с использованием способа приведения уравнения к обратному виду, или к переменной 

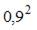
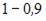





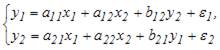
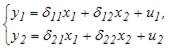
 , такая форма модели называется приведенной формой модели.
, такая форма модели называется приведенной формой модели. и спрос
и спрос  являются линейными функциями цены p, состоит из уравнений …
являются линейными функциями цены p, состоит из уравнений …
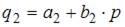



 ,
,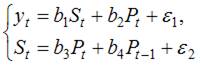
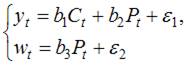
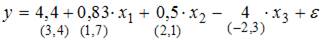 в скобках указаны значения t -статистики, соответствующие параметрам регрессии. Также известны критические значения Стьюдента для 10 степеней свободы для различных уровней значимости
в скобках указаны значения t -статистики, соответствующие параметрам регрессии. Также известны критические значения Стьюдента для 10 степеней свободы для различных уровней значимости  ,
,  ,
,  . При уровне значимости 0,1 значимыми являются параметры …
. При уровне значимости 0,1 значимыми являются параметры …

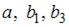

 формулируется нулевая гипотеза
формулируется нулевая гипотеза 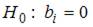 при альтернативной гипотезе
при альтернативной гипотезе  . Затем рассчитывается фактическое значение t -статистики, которое сравнивается с критическим значением Стьюдента
. Затем рассчитывается фактическое значение t -статистики, которое сравнивается с критическим значением Стьюдента  для требуемого числа степеней свободы и уровня значимости. Если
для требуемого числа степеней свободы и уровня значимости. Если  , коэффициент
, коэффициент  , коэффициент
, коэффициент 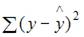 ;
;  ;
;  , где
, где 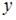 – значение зависимой переменной по исходным данным;
– значение зависимой переменной по исходным данным;  – значение зависимой переменной, вычисленное по регрессионной модели;
– значение зависимой переменной, вычисленное по регрессионной модели; 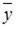 – среднее значение зависимой переменной, определенное по исходным статистическим данным. Для указанных дисперсий справедливо равенство …
– среднее значение зависимой переменной, определенное по исходным статистическим данным. Для указанных дисперсий справедливо равенство …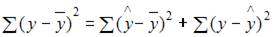



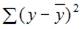 – объясненная дисперсия;
– объясненная дисперсия;  .
. (
(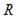 – коэффициент множественной корреляции;
– коэффициент множественной корреляции;  – коэффициент детерминации для уравнения множественной регрессии). Тогда значение коэффициента множественной корреляции
– коэффициент детерминации для уравнения множественной регрессии). Тогда значение коэффициента множественной корреляции  ]
]
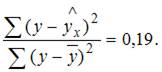 Найдем коэффициент детерминации:
Найдем коэффициент детерминации:  Вычислим коэффициент корреляции:
Вычислим коэффициент корреляции: 
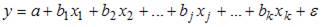 ошибкой модели является …
ошибкой модели является … – номер независимой переменной в модели, k – общее количество независимых переменных в модели); a, bj – параметры уравнения;
– номер независимой переменной в модели, k – общее количество независимых переменных в модели); a, bj – параметры уравнения; 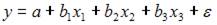 количество объясняющих переменных равно …
количество объясняющих переменных равно … построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х(1), х(2), х(3) – независимые переменные):
построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х(1), х(2), х(3) – независимые переменные):
 ;
;  ). Верным вариантом ответа является «2». Другие варианты ответов являются неверными. Теснота связи с переменной y в данном случае не рассматривается, так как переменная y не является объясняющей переменной. Поэтому другие значения в матрице, превышающие 0,7, не отражают пары коллинеарных объясняющих переменных.
). Верным вариантом ответа является «2». Другие варианты ответов являются неверными. Теснота связи с переменной y в данном случае не рассматривается, так как переменная y не является объясняющей переменной. Поэтому другие значения в матрице, превышающие 0,7, не отражают пары коллинеарных объясняющих переменных.


