Й способ вывода уравнения Эйлера
Результаты взаимодействия потока с лопаточными аппаратами могут быть получены с помощью теорем о количестве движения и о моменте количества движения. Выделим в установившемся в относительном движении потоке газа элементарную трубку тока между сечениями 1 и 2 (рис. 3.22). Согласно теореме об изменении количества движения, если скорость газа, протекающего по какому-либо каналу меняется по величине и направлению, то на стенки канала действует сила Р, равная изменению количества движения в единицу времени:
Если газ протекает через вращающееся колесо, то на последнее действует момент, равный разности моментов количества движения входящего и выходящего газа. Чтобы уравновесить этот момент, необходимо на колесо воздействовать равным моментом внешних сил, но в обратном направлении:
Учтем, что плечо r от оси вращения до линии действия силы
Проинтегрируем полученное выражение, при условии постоянства массового расхода газа между сечениями 1 и 2 (
Теоретический напор
Таким образом, воспользовавшись теоремой об изменении количества движения, получили тоже выражение (3.26). Этот вывод можно сделать еще короче, если сразу воспользоваться теоремой об изменении момента количества движения. Согласно этой теореме: производная по времени момента количества движения относительно какой-то оси равна результирующему крутящему моменту относительно этой оси.
Воспользовавшись соотношениями между сторонами треугольника скоростей (рис. 3.21), можно получить другую запись уравнения Эйлера. Из треугольника скоростей:
а т.к.
Выразим отсюда закрутку Сu:
Подставим это выражение в уравнение (3.26)
Перегруппируем слагаемые
Согласно уравнению (3.27) работа, подводимая к газу в колесе, идет на увеличение кинетической энергии в абсолютном движении (1-е слагаемое), повышение давления за счет центробежных сил (2-е слагаемое), повышение давления за счет торможения в относительном движении (3-е слагаемое). 4. Физические явления при взаимодействии потока с профилем
|

 .
.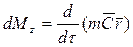
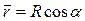 ,
, 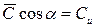 (рис. 3.23). Тогда
(рис. 3.23). Тогда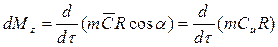 .
.

 ):
):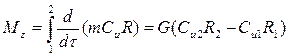 .
.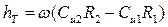 ,
,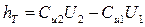 .
.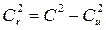 и
и 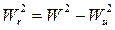 ,
,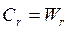 и
и 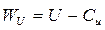 , то
, то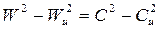 ,
, ,
,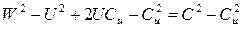 .
.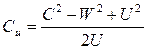 .
. .
.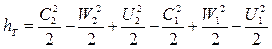 ,
,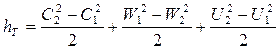 . (3.27)
. (3.27)


