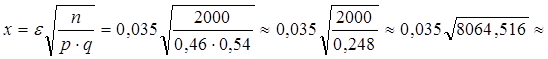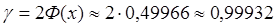ТОЧНОСТЬ И НАДЕЖНОСТЬ ОЦЕНКИ ВЕРОЯТНОСТИ

估计概率的准确性与可靠性
(ФОРМУЛА МУАВРА-ЛАПЛАСА)

13.1. Основы интервального оценивания вероятности 区间估计;

При больших объемах выборки точность и надежность статистической оценки вероятности связаны формулой Муавра-Лапласа:在大量样本统计估计概率准确性与可靠性是使用拉普拉斯公式：

,(13.1)

где Ф – функция Лапласа拉普拉斯函数, р – оценка вероятности события А 事件概率估计, q = 1 – p, ε; – точность оценки вероятности爱侣估计准确性, γ – ее надежность可靠性, n – объем выборки样本容量.

Задавая два из трех параметров ε, γ или n, можно найти значение третьего по формуле Муавра-Лапласа (13.1). Например, оценить объем выборки, требуемый для достижения заданной точности и надежности исследования.习题给出三个参数中的两个，可以根据拉普拉斯公式得出第三个。

 

13.2. Пример решения типового задания по теме
«Точность и надежность оценки вероятности»

 

Задание № 13. Вариант 1. Согласно опросу2500 человек рейтинг кандидата в депутаты муниципального образования оказался 20%. Какова точность этого опроса при его надежности 95%.据2500人问卷调查显示，20%认为市教育受欢迎。这个问卷的可靠性是95%，求准确性。

Решение. Определим значения параметров: n = 2500, γ; = 95% = 0,95, р = 20% = 0,2, следовательно, q = 1 – p = 1 - 0,2 = 0,8.

Обозначим

. (13.2)

Тогда формула Муавра-Лапласа (13.1) примет вид: . Это уравнение относительно х, причем функция Лапласа задана таблично в Прил. 2. Подставляя заданное значение надежности оценки, получаем

 

,.

По таблице Прил. 2 находим аргумент функции Лапласа, соответствующий ее значению 0,475. Это х = 1,96. Запишем соотношение (13.2):

.

Откуда

.

Значит, рейтинг кандидата в депутаты составляет 20% + 1,6%.

Задание № 13. Вариант 2. Согласно анализу2000 дипломных работ выяснилось, что 920 из них содержат серьезные грамматические ошибки. Какова надежность этого исследования при его точности 3,5%.据分析2000份毕业论文中有920份有严重的语法错误。如果这个准确性是3，5%，那么求他的可靠性。

 

Решение. Определим значения параметров: n = 2000, ε; = 3,5% = 0,035, р = = 0,46, следовательно, q = 1 – p = 1- 0,46 = 0,64.

Найдем по формуле (13.2):

.

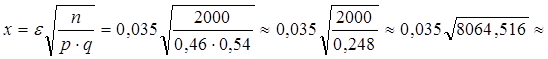
Из формулы Муавра-Лапласа (13.1) выразим надежность

.

Значение функции Лапласа найдем по таблице Прил. 2:

.

Тогда

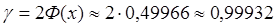
Значит, надежность проведенного исследования дипломных работ составляет 99,93%. Как и следовало ожидать, надежность такого исследования близка к 1.

13.3. Задания по теме «Точность и надежность оценки вероятности» 习题;

13.1. По результатам опроса 2500 человек законопроект поддерживают 64% взрослого населения. Какова точность этого опроса при надежности 90%? 据2500人问卷调查显示64%的成年人遵守法律条文。如果这个可靠性是90%，那么求它的准确性。	13.2. 75% из 1300 опрошенных предпочитают покупать продукты в дешевых сетевых магазинах. Какова надежность этого опроса его точности + 4%? 调查显示，1300名受访者中75%更喜欢在廉价的连锁店购买产品。如果这个问卷准确性是 + 4%，求它的可靠性。
13.3. По результатам социологи- ческого опроса из 3600 человек довольны качеством жизни 34%. Какова точность этой оценки при надежности опроса 92%? 根据社会问卷调查显示，3600人中有34%对自己的生活质量满意。如果这个估计的可靠性是92%，求它的准确性。	13.4. 42% из 1600 опрошенных студентов удовлетворены работой университетской столовой. Какова надежность полученных данных при точности + 3%? 接受调查的1600名学生中，有42%满意大学食堂工作。如果这个估计的准确性是 + 3%，那么求它的可靠性。
13.5. 90% песен, транслируемых на радио «Русский шансон», не нравятся студентам-физикам согласно опросу 1000 человек. Какова точность опроса при его надежности 88%? 物理系学生1000名，问卷显示《俄罗斯名民歌》电台播出的歌曲90%不喜欢。如果这个估计可靠性是88%，求它的准确性。	13.6. Опрос 2800 покупателей показал, что новый бренд чая «Ойстон» поддерживают 33% покупателей. Какова надежность этой оценки при допустимой точности + 4%? 据2800名消费者问卷显示，新品牌茶叶有33%喜欢。如果这个估计的准确性是 + 4%，那么求它的可靠性。
13.7. 56% из 900 испытанных образцов новой продукции джинсовой фирмы “Tears” соответствуют принятым в отрасли стандартам. Оцените точность этих испытаний при их надежности 95%. 有900人参加牛仔品牌测试调查，有56%认为符合行业标准。如果这个估计可靠性是95%，那么求它的准确性。	13.8. 41% из опробованных пачек чая бренда «Пэйл» оказались неудовлетворительного качества. Какова надежность данных проверки генеральной совокупности при ее точности + 1%? 有41%的测试茶叶包不符合质量标准。如果这个估计的准确性是 + 1%，那么求它的可靠性。
13.9. Из 1500 посетителей салонов красоты 65% ответили, что им нравятся песни, раскручиваемые «Русским радио». Какова точность этой оценки при надежности опроса 92%? 在美容院1500名消费者中表示有65%人喜欢俄罗斯广播电电台。如果这个估计的可靠性是92%，那么求它的准确性。	13.10. Опрос 3600 студентов университета показал, что здесь нравится учиться 68% из них. Какова надежность этой оценки при предполагаемой точности опроса + 2%? 有3600名大学生参加调查，其中68%表示满意学习。如果这个估计的准确性是 + 2%，求它的可靠性。