Основы применения корреляционного анализа при дихотомическом оценивании
Часто при проведении анкетирования или тестирования рассматриваются только два значения переменной, например «0» и «1» («нет» или «да»). Возникает ситуация т.н. «дихотомического оценивания». Пусть группа вопросов анкеты посвящена исследованию одного признака. Задачей корреляционного анализа в этом случае может быть оценка тесноты связи между вопросами анкеты, принадлежащими данной группе, а целью – оценка качества самой анкеты в отношении исследования рассматриваемого признака. В простейшем учебном варианте дихотомического оценивания изучают тесноту связи только двух вопросов. В качестве переменных рассматривают ответы на вопросы анкеты Х и У со значениями «0» и «1». Эти ответы были даны группой респондентов или тестируемых. Исходной в таком случае является матрица корреляции
Здесь
Построим ряды распределения случайных величин Х и У по отдельности. Для этого складываем элементы корреляционной матрицы по столбцам и по строкам:
Находим параметры, аналогичные определенным формулами (16.1) – (16.8). Математические ожидания вычисляются по формулам (5.2)
Дисперсии вычисляются по формуле (5.3)
Средне квадратические отклонения вычисляются по формулам (5.4)
Ковариация вычисляется по формуле
Коэффициент корреляции вычисляется по формуле
При дихотомическом оценивании принимается обычно градация степеней корреляции, отличная от приведенной в разд. 16 (табл. 17.1).
Таблица 17.1.
|






 . (17.1)
. (17.1)





 ,
,  ,
,  ,
,  (17.2)
(17.2) ; (17.3)
; (17.3) . (17.4)
. (17.4)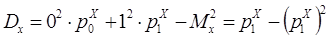 ; (17.5)
; (17.5) . (17.6)
. (17.6) ,
,  . (17.7)
. (17.7)
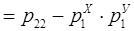 . (17.8)
. (17.8) . (17.9)
. (17.9)


