Основы точечного оценивания
Пусть дана выборка объемом n. 设给定样本容量n,
Характеристики случайной величины, найденные по выборке называются выборочными характеристиками. Рассмотрим по 4 выборочные оценки математического ожидания и среднеквадратического отклонения.点估计是依据样本估计总体分布中所含的未知参数或未知参数的函数。通常它们是总体的某个特征值,如数学期望、方差和相关系数等。点估计问题就是要构造一个只依赖于样本的量,作为未知参数或未知参数的函数的估计值。 Точечные оценки математического ожидания: 1. Выборочное среднее (среднее арифметическое):样本平均值
med = 3. Полусумма квартилей:四分位数之和的一半
где квартили вычисляются по формулам (10.4), (10.5). 4. Полусумма экстремальных значений:极端值之和的一半
Точечные оценки средне квадратического отклонения:点估计四分位数均值的偏离 1. Выборочное отклонение:样本偏差 Сначала находят выборочную дисперсию:首先处于样本方差
Выборочное отклонение:
2. Абсолютное отклонение:绝对偏差
3. Интерквартильная широта:四分位数间距
4. Размах:范围
Основные свойства точечных оценок:点估计的基本性质 1. Состоятельность оценки означает, что с увеличением объема выборки оценка стремится к самой величине. Все рассмотренные выше статистические оценки математического ожидания и отклонения являются состоятельными. 2. Несмещенность оценки означает, что математическое ожидание оценки равно математическому ожиданию самой величины. Все рассмотренные оценки математического ожидания являются несмещенными, а все оценки отклонения – смещенными. Для получения несмещенных оценок их нормируют. Универсально нормируется только выборочное отклонение, остальные нормировочные коэффициенты зависят от предполагаемого вида закона распределения случайной величины. Несмещенное отклонение вычисляется по формуле:
3. Робастность оценки в узком смысле означает устойчивость к выбросам случайных данных. Робастные оценки не содержат экстремальных элементов выборки.
12.2. Пример решения типового задания по теме Задание № 12. Дана выборка. Найти выборочное среднее, медиану, полусумму квартилей, полусумму экстремальных значений, выборочную дисперсию, выборочное отклонение, абсолютное отклонение, интерквартильную широту, размах. Расположить оценки математического ожидания и отклонения в порядке возрастания. Сделать вывод о степени близости оценок. Указать состоятельность, несмещенность и робастность всех найденных оценок выборочных характеристик. Найти несмещенное выборочное отклонение.给定样本。找出样本平均数,中位数,四分位数之和的一半,极端值之和的一半,样本方差,绝对偏差,四分位数间距,范围。找到升序排列的数学期望估计和偏差,得出接近额度值程度的结论。指出全部指定样本一致性,无偏性,有效性。找出一致估计偏差。 Решение. Объем выборки n = 25. Построим вариационный ряд – упорядочим выборку по возрастанию (см. пример в разделе 10).
Найдем точечные оценки математического ожидания: 1. Найдем выборочное среднее по формуле (12.1):
2. Найдем выборочную медиану по формуле (12.2) аналогично примеру в разделе 10: med = 5. 3. Найдем полусумму квартилей по формуле(12.3). Сами квартили находим по аналогии с примером раздела 10: Тогда 4. Найдем полусумму экстремальных значений по формуле (12.4). Сами экстремальные значения определяются как в примере раздела 10:
Тогда Расположим оценки математического ожидания по возрастанию: . Видно, что оценки математического ожидания хорошо согласованы, за исключением, может быть, медианы, значение которой указывает на несимметричный характер распределения значений выборки. Все оценки математического ожидания являются состоятельными и несмещенными. Робастными будут оценки, при вычислении которых не используются экстремальные значения. Это медиана med, формула (12.2) и полусумма квартилей Найдем точечные оценки средне квадратического отклонения: 1. Выборочную дисперсию находим по формуле (12.5):
Выборочное отклонение вычисляется по формуле (12.6):
2. Абсолютное отклонение находим по формуле (12.7):
3. Интерквартильную широту находим по формуле (12.8):
4. Размах находим по формуле (12.9):
Расположим оценки отклонения по возрастанию:
Видно, что не все оценки отклонения хорошо согласованы. Но, во всяком случае, порядок возрастания различных оценок математического ожидания совпадает с порядком возрастания сходственных оценок отклонения (медиана – абсолютное отклонение, выборочное среднее – выборочное отклонение, полусумма квартилей – интерквартильная широта, полусумма экстремальных значений – размах). Кроме того, наиболее грубые из оценок – размах и полусумма экстремальных значений, действительно в наибольшей степени отличаются от группы остальных оценок. Все оценки отклонения являются состоятельными и смещенными. Несмещенное выборочное отклонение находим по формуле (12.10):
Единственной робастной оценкой отклонения является интерквартильная широта, при вычислении которой не используются экстремальные элементы выборки. 12.3. Задания по теме «Точечные оценки выборочных Текст задания. Дана выборка. 给定样本。 1) Найти выборочное среднее, медиану, полусумму квартилей, полусумму экстремальных значений, выборочную дисперсию, выборочное отклонение, абсолютное отклонение, интерквартильную широту, размах.找出样本平均数,中位数,四分位数之和的一半,极端值之和的一半,样本方差,绝对偏差,四分位数间距,范围。 2) Расположить оценки математического ожидания и отклонения в порядке возрастания. 找到升序排列的数学期望估计和偏差。 3) Сделать вывод о степени близости оценок. 得出接近额度值程度的结论。 4) Указать состоятельность, несмещенность и робастность всех найденных оценок выборочных характеристик. Найти несмещенное выборочное отклонение.指出全部指定样本一致性,无偏性,有效性。找出一致估计偏差。 Таблица 12.1 Варианты задания
|




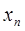
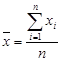 . (12.1)
. (12.1) 2. Выборочная медиана – вычисляется по формуле (10.2):样本中位数
2. Выборочная медиана – вычисляется по формуле (10.2):样本中位数 . (12.2)
. (12.2) , (12.3)
, (12.3) . (12.4)
. (12.4) . (12.5)
. (12.5) . (12.6)
. (12.6) . (12.7)
. (12.7)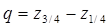 . (12.8)
. (12.8) . (12.9)
. (12.9) . (12.10)
. (12.10)
 .
. ,
,  .
. .
. ,
,  .
.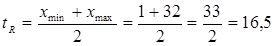 .
.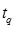 , формула (12.3).
, формула (12.3).
 .
.
 .
. .
. .
.



