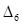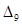Основы проверки гипотезы о нормальном распределении
Для проверки гипотезы о нормальном распределении генеральной совокупности (случайной величины Х) традиционно используется критерий Пирсона. Проще всего сравнить экспериментальные интервальные частоты, полученные на основе группировки выборки (разд. 11) и теоретические частоты нормально распределенной случайной величины, полученные для выборки того же объема с теми же самыми интервалами группировки. Эти данные сводятся в таблицу:
Вычисляется выборочное значение критерия
Правило проверки гипотезы о нормальном распределении генеральной совокупности состоит в следующем. Назначается или выбирается уровень значимости α;. Это величина, связанная с надежностью проверки статистической гипотезы. Можно считать, что меньшее значение α; соответствует большему уровню надежности. Находят число степеней свободы k. Обычно k = s – 3. Действительно, число интервалов надо уменьшить на 3 связи. Одна из них – условие нормировки На основании значений α; и k по таблице распределения
то гипотеза о нормальном распределении генеральной совокупности принимается на уровне значимости α;. В противном случае гипотеза отвергается. 15.2. Пример решения типового задания по теме «Критерий Пирсона» Задание № 15. На уровне значимости α; = 0,05 установить по критерию Пирсона случайность или значимость расхождения между экспериментальными
Решение. Проверим условие нормировки
Значит, объем выборки n = 50. Проверим условие нормировки для теоретических интервальных частот:
Таким образом, экспериментальная и нормально распределенная выборки имеют одинаковый объем и можно проводить проверку по критерию Пирсона. Найдем выборочное значение критерия
= 4,77.
Определим значения параметров проверки. α; = 0,05, значит β = 1 – α; = 1 – 0,05 = 0,95. Число интервалов s = 5. Значит, число степеней свободы k = s – 3 = 5 – 3 = 2. По таблице прил. 3 находим значение критерия Пирсона
Согласно правилу проверки гипотезы на основании критерия Пирсона (15.2) получаем: 4,77 < 5,99. Таким образом, правило проверки (15.2) выполняется. Это означает, что расхождения между экспериментальными и теоретическими данными носит случайный характер. Следовательно, на уровне значимости 0,05 можно принять гипотезу о нормальном распределении генеральной совокупности (исследуемой случайной величины Х).
15.3. Задания по теме «Критерий Пирсона» Текст задания. На уровне значимости α; установить по критерию Пирсона случайность или значимость расхождения между экспериментальными
Таблица 15.1
Варианты задания
Продолжение табл. 15.1
16. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ 相关分析;
|

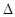
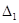
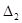
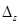
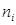
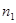

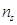
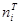
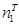

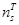

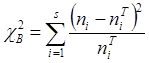 . (15.1)
. (15.1)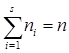 – объем выборки. Две другие связи означают, что математическое ожидание и средне квадратическое отклонение (необходимые параметры нормального распределения) оцениваются на основании данных той же выборки. Без знания этих оценок невозможно найти теоретические значения интервальных частот
– объем выборки. Две другие связи означают, что математическое ожидание и средне квадратическое отклонение (необходимые параметры нормального распределения) оцениваются на основании данных той же выборки. Без знания этих оценок невозможно найти теоретические значения интервальных частот 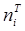 .
. , где β = 1 – α;. Если
, где β = 1 – α;. Если , (15.2)
, (15.2) и теоретическими
и теоретическими 
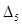
 .
. .
.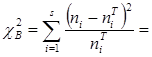
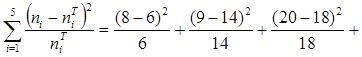
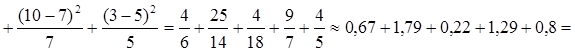
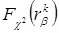
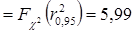 .
.