Основы группировки статистических данных
Для придания данным выборки большей наглядности при их графическом представлении принято строить группированный статистический ряд. Пусть дана выборка, построен вариационный ряд.为了研究样本总体分布的性质,可以得到很多观察值,可直接通过建立频率直方图对其进行研究。
Построим группированный ряд, состоящий из k интервалов. Найдем шаг h – длину одного интервала, предполагая равномерную группировку, т.е. разбиение на интервалы равной длины. По формулам (10.1) найдем экстремальные элементы:整理数据,有k个小区间,区间长度为h,每个区间等距,根据公式可得出小区间的端点,称为组限:
 , ,  . .
Тогда
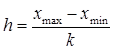 . (11.1) . (11.1)
Границы интервалов 组距公式  вычисляются по формулам: вычисляются по формулам:
 . (11.2) . (11.2)
Соответственно, оказывается  . .
Находятся интервальные частоты 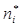 - это количество элементов выборки, попавших на интервал - это количество элементов выборки, попавших на интервал  . Для углубленных статистических исследований вычисляются относительные частоты . Для углубленных статистических исследований вычисляются относительные частоты  и относительные плотности частот и относительные плотности частот  . На основании этих данных строят группированный ряд:数出落在每个小区间的数据的频数f,算出频率 . На основании этих данных строят группированный ряд:数出落在每个小区间的数据的频数f,算出频率
Графическое изображение группированного ряда – гистограмма. В углубленных статистических исследованиях по оси У гистограммы откладывают относительные плотности частот. Это обязательно, во-первых, при неравномерной группировке (при изменяющемся шаге h), во-вторых, при необходимости расчета интервальных выборочных характеристик.
11.2. Пример решения типового задания по теме
«Группированный статистический ряд»
Задание № 11. Дан вариационный ряд.
0,3,5,11,11,15,15,16,19,19,20,20,21,22,23,23,25,25,27,27,27,29,31,32,32,36,36,38,39,39,43,43,44,47,50.
Составить группированный ряд (пять интервалов), построить гистограмму, выдвинуть гипотезу о возможном законе распределения случайной величины. Приблизительно нанести на гистограмму теоретическую кривую предполагаемого распределения.
Решение. Объем выборки n = 25. Число интервалов для группировки k = 5. Экстремальные элементы  , ,  . Найдем шаг разбиения по формуле (11.1): . Найдем шаг разбиения по формуле (11.1):
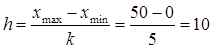 . .
Тогда границы интервалов можно найти по формуле (11.2) с учетом того, что  : :
 ; ;
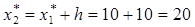 ; ;
 ; ;
 ; ;
 . .
Устно подсчитывая интервальные частоты, можем построить группированный ряд

| [0, 10)
| [10, 20)
| [20, 30)
| [30, 40)
| [40, 50)
| 
|
|
|
|
|
|
Строим гистограмму, откладывая по оси Х интервалы изменения значений случайной величины, по оси У – интервальные частоты. Поскольку углубленный статистический анализ не предполагается, то относительные частоты и плотности частот не вычисляются. В нашем случае вид гистограммы при таком упрощении не изменяется, изменяется только масштаб по оси У, который не влияет на выдвигаемое предположение о законе распределения случайной величины. Гистограмма приведена на рис. 11.1.

Рис. 11.1.Гистограмма
На основании вида гистограммы можно выдвинуть гипотезу о нормальном распределении случайной величины. Кривая, имитирующая кривую Гаусса, эскизно нанесена на гистограмму. Разумеется, это предположение является лишь предварительной гипотезой, которая может быть принята или отвергнута только на основании углубленного статистического анализа с вычислением выборочных характеристик и проведением процедуры проверки статистической гипотезы на основе выбранного критерия.
11.3. Задания по теме «Группированный статистический ряд»
Текст задания. Дан вариационный ряд. Составить группированный ряд (пять интервалов), построить гистограмму, выдвинуть гипотезу о возможном законе распределения случайной величины. Приблизительно нанести на гистограмму теоретическую кривую предполагаемого распределения.
Таблица 11.1
Варианты задания
| 11.1.
| 11.2.
| | 1,1,2,2,3,3,4,5,6,7,8,10,10,12,12,13,
14,15,18,18,21,21,21,25,25,25,28,29,32, 33,33,37,38,45,50
| 1,2,3,4,5,5,5,10,10,11,12,18,19,21,23,
23,27,28,30,35,43,43,45,46,48,50,50,58,64,68,70,73,78,83,100
| | 11.3.
| 11.4.
| | 1,2,12,12,18,18,19,21,21,23,23,25,
25,28,29,31,31,31,31,31,34,34,36,36,36, 39,39,39,41,45,45,47,48,49,50
| 1,18,23,23,30,35,39,45,45,46,47,50,51,
51,59,62,62,62,63,65,66,67,70,76,76,77,78,79,81,82,86,88,89,95,100
| | 11.5.
| 11.6.
| | 1,1,2.2,5,8,9,11,12,15,15,18,18,19,
19,21,25,25,28,29,32,34,35,38,39,41, 46,46,46,47,48,48,49,50
| 1,2,5,10,15,16,18,21,22,25,29,30,30,36,39,41,44,50,50,56,56,61,67,69,76,78,81,86,86,87,88,89,90,91,100
| | 11.7.
| 11.8.
| | 1,2,3,5,6,7,8,9,12,13,15,15,17,21,23,24,24,25,27,27,31,32,33,34,35,36,36,37, 37,42,45,45,45,49,50
| 1,2,5,7,9,10,10,18,25,25,30,35,39,41,41,50,55,55,59,59,61,62,65,65,70,70,71,76,79,81,86,90,90,98,100
| | 11.9.
| 11.10.
| | 1,2,3,4,5,11,11,13,13,14,14,18,22,22, 22,23,23,24,24,25,25,25,28,28,28,28, 29,31,31,34,34,37,43,43,50
| 1,2,3,13,18,23,23,24,25,25,39,39,41,41,41,43,44,45,45,45,50,50,56,56,57,58,59,65,67,70,76,76,87,90,100
|
12. ТОЧЕЧНЫЕ ОЦЕНКИ ВЫБОРОЧНЫХ
ЧИСЛОВЫХ ХАРАКТЕРИСТИК 点估计;

Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений...
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|
Мелоксикам (Мовалис) Групповая принадлежность
· Нестероидное противовоспалительное средство, преимущественно селективный обратимый ингибитор циклооксигеназы (ЦОГ-2)...
Менадиона натрия бисульфит (Викасол) Групповая принадлежность
•Синтетический аналог витамина K, жирорастворимый, коагулянт...
Разновидности сальников для насосов и правильный уход за ними
Сальники, используемые в насосном оборудовании, служат для герметизации пространства образованного кожухом и рабочим валом, выходящим через корпус наружу...
|
Случайной величины Плотностью распределения вероятностей непрерывной случайной величины Х называют функцию f(x) – первую производную от функции распределения F(x):
Понятие плотность распределения вероятностей случайной величины Х для дискретной величины неприменима...
Схема рефлекторной дуги условного слюноотделительного рефлекса При неоднократном сочетании действия предупреждающего сигнала и безусловного пищевого раздражителя формируются...
Уравнение волны. Уравнение плоской гармонической волны. Волновое уравнение. Уравнение сферической волны Уравнением упругой волны называют функцию , которая определяет смещение любой частицы среды с координатами относительно своего положения равновесия в произвольный момент времени t...
|
|





 ,
,  .
.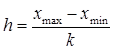 . (11.1)
. (11.1) вычисляются по формулам:
вычисляются по формулам: . (11.2)
. (11.2) .
.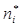 - это количество элементов выборки, попавших на интервал
- это количество элементов выборки, попавших на интервал  и относительные плотности частот
и относительные плотности частот  . На основании этих данных строят группированный ряд:数出落在每个小区间的数据的频数f,算出频率
. На основании этих данных строят группированный ряд:数出落在每个小区间的数据的频数f,算出频率







 ,
,  . Найдем шаг разбиения по формуле (11.1):
. Найдем шаг разбиения по формуле (11.1):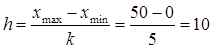 .
. :
: ;
;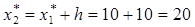 ;
; ;
; ;
; .
.




