Пусть происходит большое число опытов n. В каждом из опытов событие А может появиться с небольшой вероятностью р. Величина我们进行大量的实验,用n表示,每次独立的实验为事件A,发生事件A的 概率为p,那么
 (7.1)
(7.1)
в пределе при  связана с интенсивностью наступления события А. Тогда случайная величина Х – число появлений события А распределена по закону Пуассона.当n趋向无限大时,事件A发生的概率也会频繁,那么事件A发生的随机变量X的分布将符合泊松定律。
связана с интенсивностью наступления события А. Тогда случайная величина Х – число появлений события А распределена по закону Пуассона.当n趋向无限大时,事件A发生的概率也会频繁,那么事件A发生的随机变量X的分布将符合泊松定律。
 . (7.2)
. (7.2)
7.2. Пример решения типового задания по теме
«Распределение Пуассона»例题详解;
Задание № 7. Только 2 из 500 метеоритов, достигающих поверхности Земли, весят больше 5 г. Какова вероятность, что из 750 метеоритов, упавших за неделю на территории Челябинской области сравнительно крупными (массой больше 5 г.) будут: 重量大于5公斤的陨石每500颗陨石只有2颗到达地球表面,在本周坠落在750颗陨石中本周坠落在车里雅宾斯克地区,重量在5g以上的:
1. Больше 3 метеоритов? 大于3颗
2. От 2 до 4 метеоритов? 2-4颗
3. Хотя бы 1 метеорит? 至少一颗
Решение. Определим параметры закона Пуассона. Вероятность падения сравнительно крупного метеорита 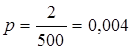 . Обнаружено на территории Челябинской области n = 750 метеоритов. Тогда, согласно формуле (7.1),
. Обнаружено на территории Челябинской области n = 750 метеоритов. Тогда, согласно формуле (7.1), 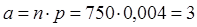 .根据定律求参数,比较大的陨石的坠落概率为
.根据定律求参数,比较大的陨石的坠落概率为 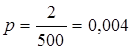 。在车里雅宾斯克地区坠落的陨石N = 750。根据公式7.1 得出
。在车里雅宾斯克地区坠落的陨石N = 750。根据公式7.1 得出
Найдем вероятность, что крупных метеоритов будет больше 3. По формуле вероятности противоположного события: 我们可以通过求相反事件发生的概率,求得较大的陨石坠落的概率
 .
.
 .
.
Искомая вероятность представляет собой сумму вероятностей того, что случайная величина Х принимает фиксированные значения. 所需要的概率是一个随机变量X取固定值的概率时的总和
Формулой суммы вероятностей можно пользоваться именно в таком виде, поскольку считается, что случайная величина Х, распределенная по закону Пуассона, принимает любое свое значение независимо от других принятых ею значений. 概率之和公式可以以这种形式使用,因为它认为,随机变量X是按照泊松分布规律,可以取任何值,不受其他值约束。
Вероятности того, что случайная величина Х принимает фиксированные значения вычисляются по формуле (7.2):随机变量X根据固定公式可求出概率:
 ,
,
 ,
,
 ,
,
 .
.
Тогда 那么
 .
.
Соответственно相应的
 .
.
Найдем вероятность, что крупных метеоритов будет от 2 до 4: 大陨石将会坠落2到4颗的概率:
 .
.
Обратим внимание, что часть вероятностей уже найдена. Оставшуюся неопределенной вероятность  находим по формуле (7.2):部分概率已经求出,未知概率
находим по формуле (7.2):部分概率已经求出,未知概率  ,由下式求出:
,由下式求出:
 .
.
Тогда
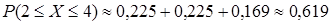 .
.
Найдем вероятность, что крупных метеоритов будет хотя бы 1. Это  . По формуле вероятности противоположного события:
. По формуле вероятности противоположного события:
求陨石至少1颗坠落的概率,这个可按照相反的事件的概率公式求出:
 .
.
Результат, как обычно, не противоречит житейской логике. Действительно, если из 500 метеоритов в среднем 2 относительно крупные, то среди 750 с большой вероятностью найдется хотя бы 1 относительно крупный.
得出结果不违背逻辑。事实上,如果每500颗中有2颗比较大的陨石坠落,那么 750颗陨石很可能会发现至少有一个比较大的。
7.3. Задания по теме «Распределение Пуассона» 习题;
| 7.1. Вероятность появления бриллианта высшего качества 0,3%.
Какова вероятность, что среди 900 бриллиантов фирмы «Бриз»:
1. Больше 2 высшего качества?
2. От 1 до 4 высшего качества?
3. Меньше 3 высшего качества?
出现最高质量的钻石概率是0.3 %。在这样的概率下,«Бриз»公司900颗钻石中,出现高质钻石有:
1.大于两颗?
2.1-4颗?
3.少于3颗?
| 7.2. Только 0,15% альпинистов восходят на Эверест. Какова вероятность, что из 600 членов клуба «Гора»:
1. Кто-либо восходил на Эверест?
2. Более 3-х восходили на Эверест?
3. От 2 до 3 восходили на Эверест?
只有0.15 %的登山者能登上珠穆朗玛峰。在这种情况下,600名登山俱乐部成员中能登上珠穆朗玛峰有:
1.至少一人?
2.大于三人?
3.至少3人?
|
| 7.3. Вероятность встретить зайца в городе 0,1% в год. В городе живут 400 зайцев. С какой вероятностью можно увидеть за год:
1. Больше 1 зайца?
2. От 1 до 3 зайцев?
3. Хотя бы 1 зайца?
一年中在城市中遇到野兔的概率是0.1%,在城市中有着400只野兔。这种情况下一年中能看到多少只野兔:
1. 大于一只?
2. 1-3只?
3. 至少一只?
| 7.4. В лесу - 0,8% деревьев старше 200 лет. Исследовали 400 деревьев. Какова вероятность, что было обнаружено:
1. Только 3 двухсотлетних?
2. Больше 2 двухсотлетних?
3. Ни одного двухсотлетнего?
在森林中有0,8%的树超过200年,在400棵树中调查。能够发现:
1.只有3棵200年以上的树?
2.大于2棵200年以上的树?
3.没有200年以上的树?
|
| 7.5. 0,3% лингвистов знают больше 10 языков. На конференцию собрались 250 лингвистов. Какова вероятность, что больше 10 языков знают:
1. Хотя бы 1?
2. Хотя бы 3?
3. Меньше 2?
有0,3%的语言学家知道超过10种以上的语言。这次会议汇集了250名语言学家。在这种概率下,知道超过10种语言的语言学家:
1.至少一位?
2.至少3位?
3.少于两位?
| 7.6. Вероятность, что в семье 4 и больше детей 0,4%. Какова вероятность, что среди 700 обследованных семей больше 4 детей имеют:
1. Больше 4 семей?
2. От 1 до 3 семей?
3. Не больше 2 семей?
0,4%的家庭中有4个或超过4个孩子。在这种情况下,调查700个家庭中有超过4个孩子:
1. 大于4个家庭?
2. 1个至3个家庭?
3. 不会超过2个家庭?
| |
| 7.7. Менеджмент считается эффективным, если вероятность ошибок менеджеров, связанных с существенными потерями составляет 0,03% в год. В компании 1500 менеджеров. Какова вероятность, что в год допустят серьезные ошибки: 如果一年中管理人员出现严重错误给公司带来0.03%的损失,那么管理人员被视为优秀的。公司中有1500名管理人员。在这种情况下一年中犯了严重错误的管理人员:
1. Хотя бы 1 из них? 至少1名
2. 1 или 2? 1名或两名
3. Более 3?超过3人
| 7.8. Только 0,02% иностранных студентов в России не имеют адаптационных трудностей. Какова вероятность того, что из 2000 иностранных студентов не имели адаптационных трудностей:
1. Хотя бы 1?
2. Больше 3?
3. Меньше 2?
只有0.02%的外国学生在俄罗斯没有适应上得困难。在这种情况下,2000名外国学生中没有适应上困难的有:
1. 至少1名?
2. 大余3名?
3. 少于2名?
| |
| 7.9. Вероятность появления 6-ти лепесткового цветка сирени 0,06%. На ветке в соцветиях 1000 цветочков. Какова вероятность:
1. Не найти 6-ти лепестковых?
2. Найти 1 или 2 6-ти лепестковых?
3. Найти больше 4 6-ти лепестковых?
出现6色花瓣花的概率是0,06%。在1000支中研究,在这种情况下:
1.没有6色花瓣花?
2.找到一到两支6色花瓣花?
3. 找到大于四支6色花瓣花?
| 7.14. Обычно на рейс опаздывает 1,5% пассажиров. На рейс куплено 300 билетов. Какова вероятность того, что на рейс опоздают:
1. Менее 3 пассажиров?
2. Хотя бы 1 пассажир?
3. Один или 2 пассажира?
通常情况下,有1,5%的乘客会在乘坐航班时迟到。一次航班有300张票,在这种情况下,航班上迟到的乘客:
1. 少于三名?
2. 至少1位?
3. 1名或者2名?
| |

 (7.1)
(7.1) связана с интенсивностью наступления события А. Тогда случайная величина Х – число появлений события А распределена по закону Пуассона.当n趋向无限大时,事件A发生的概率也会频繁,那么事件A发生的随机变量X的分布将符合泊松定律。
связана с интенсивностью наступления события А. Тогда случайная величина Х – число появлений события А распределена по закону Пуассона.当n趋向无限大时,事件A发生的概率也会频繁,那么事件A发生的随机变量X的分布将符合泊松定律。 . (7.2)
. (7.2)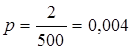 . Обнаружено на территории Челябинской области n = 750 метеоритов. Тогда, согласно формуле (7.1),
. Обнаружено на территории Челябинской области n = 750 метеоритов. Тогда, согласно формуле (7.1), 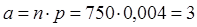 .根据定律求参数,比较大的陨石的坠落概率为
.根据定律求参数,比较大的陨石的坠落概率为  .
. .
. ,
, ,
, ,
, .
. .
. .
. .
. находим по формуле (7.2):部分概率已经求出,未知概率
находим по формуле (7.2):部分概率已经求出,未知概率  ,由下式求出:
,由下式求出: .
.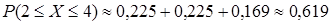 .
. . По формуле вероятности противоположного события:
. По формуле вероятности противоположного события: .
.


