事件的发生与总和
2.1. Основы алгебры событий 基本事件代数;
Пусть событие А 1  может произойти с вероятностью р или не произойти с вероятностью q = 1-p. Пусть опыт, в котором может появиться событие А 1
может произойти с вероятностью р или не произойти с вероятностью q = 1-p. Пусть опыт, в котором может появиться событие А 1  , повторяется два раза. Тогда, принимая во внимание правила умножения и сложения вероятностей, можно найти вероятности следующих событий: 让事件 А 1可能发生概率为 р 或者不会发生的概率为 q = 1-p 。进行事件 А 1的实验,重复两次。那么有以下概率加法与乘法的规则:
, повторяется два раза. Тогда, принимая во внимание правила умножения и сложения вероятностей, можно найти вероятности следующих событий: 让事件 А 1可能发生概率为 р 或者不会发生的概率为 q = 1-p 。进行事件 А 1的实验,重复两次。那么有以下概率加法与乘法的规则:
А – событие А 1  не произойдет ни разу,
не произойдет ни разу,  ;一次都不发生,
;一次都不发生,
В – событие  произойдет только 1 раз,
произойдет только 1 раз,  ;只发生一次
;只发生一次
С – событие А 1  произойдет 2 раза,
произойдет 2 раза, 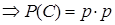 ;发生两次
;发生两次
D – событие  произойдет хотя бы 1 раз, это событие противоположно событию А,
произойдет хотя бы 1 раз, это событие противоположно событию А,  . 至少发生一次,这是对立事件。
. 至少发生一次,这是对立事件。
Пусть теперь опыт, в котором может появиться событие 
 , повторяется три раза. Тогда, принимая во внимание правила умножения и сложения вероятностей, можно найти вероятности следующих событий:现在开始进行事件 А 1实验,重复三次。那么那么有以下概率加法与乘法的规则:
, повторяется три раза. Тогда, принимая во внимание правила умножения и сложения вероятностей, можно найти вероятности следующих событий:现在开始进行事件 А 1实验,重复三次。那么那么有以下概率加法与乘法的规则:
А – событие  не произойдет ни разу,
не произойдет ни разу, 
 ;一次都不发生
;一次都不发生
В – событие  произойдет только 1 раз,
произойдет только 1 раз, 

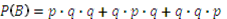 ;只发生一次
;只发生一次
С – событие  произойдет 2 раза,
произойдет 2 раза, 
 ;发生2次
;发生2次
D – событие  произойдет 3 раза,
произойдет 3 раза, 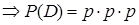 ;发生3次
;发生3次
E – событие  произойдет хотя бы 2 раза, значит оно произойдет или 2 раза или 3 раза,
произойдет хотя бы 2 раза, значит оно произойдет или 2 раза или 3 раза,  ;至少发生2次,也就是说可能2次可能3次
;至少发生2次,也就是说可能2次可能3次
F – событие  произойдет хотя бы 1 раз, это событие противоположно событию А,
произойдет хотя бы 1 раз, это событие противоположно событию А,  .至少发生1次,这是对立事件。
.至少发生1次,这是对立事件。
Рассмотрим более сложную ситуацию. Пусть событие  может произойти с вероятностью
может произойти с вероятностью 
 или не произойти с вероятностью
или не произойти с вероятностью  . Независимо от этого событие
. Независимо от этого событие 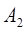 может произойти с вероятностью
может произойти с вероятностью 
 или не произойти с вероятностью
или не произойти с вероятностью  . Тогда, принимая во внимание правила умножения и сложения вероятностей, можно найти вероятности следующих событий:分析更复杂的情况。让事件
. Тогда, принимая во внимание правила умножения и сложения вероятностей, можно найти вероятности следующих событий:分析更复杂的情况。让事件  发生概率为
发生概率为  或者不发生概率为
或者不发生概率为  。独立事件
。独立事件 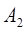 发生概率为
发生概率为  或者不发生概率为
或者不发生概率为  ,那么
,那么
А – ни одно из событий  и
и 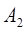 не произойдет,
не произойдет,  ;没有任何事件发生
;没有任何事件发生
В – произойдет только одно событие 
 или
или 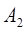 ,
, 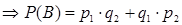 ;只有其中一种发生
;只有其中一种发生
С – произойдут оба события 
 и
и 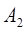 ,
,  ;两种同时发生
;两种同时发生
D – произойдет хотя бы одно событие 
 или
или 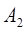 , или оба вместе, это событие противоположно событию А,
, или оба вместе, это событие противоположно событию А,  .至少发生其中一种,或者同时发生,这是对立事件。
.至少发生其中一种,或者同时发生,这是对立事件。
2.2. Решение типового задания по теме
«Сумма и произведение событий» 例题解答;
Задание № 2. Студент может получить на экзамене пятерку с вероятностью 60%, четверку – с вероятностью 30% и тройку с вероятностью 10%. Студенту надо сдать 3 экзамена. Найти вероятности событий:学生在考试中可能获得5分的概率为60%,得4分概率为30%,得3分概率为10%。学生需要参加3门考试。求事件概率:
А – студент получит все пятерки;全部得5分
В – студент получит ровно 2 пятерки; 2个5分
С – студент получит ровно 1 пятерку;1个5分
D – студент получит хотя бы 1 пятерку;至少1个5分
Е – студент получит хотя бы 2 пятерки;至少2个分
F – студент получит все разные оценки;不同分数
G – студент получит две пятерки и четверку;2个5分和1个4分
Н – студент получит тройку на первом экзамене, четверку – на втором и пятерку на третьем.第一门3分,第二门4分,第3门5分。
Решение. Обозначим: p 1 = 0,6 – вероятность получить пятерку;  = 1 – 0,6 = 0,4 – вероятность не получить пятерки;
= 1 – 0,6 = 0,4 – вероятность не получить пятерки;  = 0,3 – вероятность получить четверку,
= 0,3 – вероятность получить четверку,  = 1 – 0,3 = 0,7 – вероятность не получить четверки;
= 1 – 0,3 = 0,7 – вероятность не получить четверки;  = 0,1 – вероятность получить тройку;
= 0,1 – вероятность получить тройку; 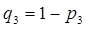 = 1 – 0,1 = 0,9 – вероятность не получить тройки.
= 1 – 0,1 = 0,9 – вероятность не получить тройки.
Тогда
 ;
;
 = 0,432;
= 0,432;
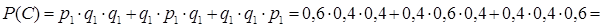 =0,288;
=0,288;
 ;
;
 ;
;

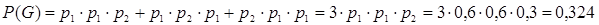 ;
;
 .
.
Вероятность получить пятерку на экзамене достаточно высокая, поэтому, наибольшей будет вероятность события D – получения хотя бы одной пятерки. В то же время, очевидно, что вероятность события F – получения всех различных оценок – в 6 раз больше вероятности более редкого события Н – получения этих же оценок, но в определенном порядке.获得5分的概率是很高的,所以事件D发生的概率最大。
2.3. Задания по теме «Сумма и произведение событий»习题;
| 2.1. На прогулочном корабле 30% немцев, 20% поляков, 10% словаков, остальные – русские. Какова вероятность, что из двоих, прыгнувших в воду:在游船上30%德国人,20%波兰人,10%斯拉夫人,其他是俄罗斯人。求游船上两人中,以下事件概率:
А – все представители разных народов,全部都是不同国籍
В – все русские,全部是俄罗斯人
С – все немцы,全部德国人
D – 1 поляк и 1 словак,一个波兰人一个斯拉夫人
Е – первый поляк,第一个是波兰人
F – хотя бы 1 поляк.至少1个波兰人。
| 2.2.По статистике10% потребителей слабоокрашенных газированных напитков предпочитают содовую, 20% – спрайт, остальные – лимонную фанту. Найти вероятность, что в компании из трех друзей предпочитают:根据统计,10%的弱酸饮料是苏打水,20%雪碧,其他事芬达。求3瓶套装组成的概率:
А – хотя бы 1 - содовую,至少1瓶苏打水
В – хотя бы 2 лимонную фанту,至少2瓶芬达
С – менее двух - спрайт,2瓶以下雪碧
D – не более 1 - лимонную фанту,不超过1瓶芬达
Е – все разное,全部不同
F – первый фанту и еще 1 спрайт.第1瓶芬达和1瓶雪碧。
|
| 2.3. 44% доступных в отеле телеканалов – музыкальные, причем каналы случайным образом меняются на кнопках испорченного пульта. Найти вероятности того, что при трех нажатиях кнопки пульта попадешь на музыкальные каналы:44%接收到了频道是音乐台,用遥控器换台,频道设置是随机的。求三次换台,换到音乐台的概率:
А –3 раза,3次
В – только 1 раз,1次
С – хотя бы 1 раз,至少1次
D – 1-й и 3-й раз,1次和3次
Е – хотя бы 2-й раз,至少2次
F – ни разу.1次都没有
| 2.4. Три локатора следят за появлением самолетов. Первый локатор обнаруживает самолет с вероятностью 0,78, второй – 0,67, а третий – 0,41. Найти вероятность того, что появившийся самолет будет обнаружен: 三部定位器观测飞机出现情况,第一部检测概率为0,78,第二部检测概率为0,67,第三步检测概率为0,41。求出现飞机检测的概率:
А – хотя бы одним из локаторов,至少一部
В – только одним локатором,只有一部
С – хотя бы 2 локаторами,至少两部
D – менее чем 2 локаторами,不到两部
Е – ровно 2 локаторами,正好两部
F – всеми 3 локаторами.三部都检测
|
| 2.5. Судно может встать под разгрузку на любой из 4 причалов. К моменту прихода судна 1-ый причал будет свободен с вероятностью 0,9, 2-ой – 0,5, третий – 0,4 и четвертый – 0,2. Какова вероятность, что в момент прихода судна будет свободен:货轮可以停靠在4个码头的其中任意一个,货轮抵达的时刻,第一个码头空闲概率是0,9,第二个空闲是0,4,第四个空闲是0,2,以下情况码头空闲的概率:
А – хотя бы один причал,至少1个
В – только один причал,只有1个
С – хотя бы два причала,至少2个
D – хотя бы второй и третий причалы? 至少第二个和第三个
| 2.6. В лесу 60% хвойных деревьев, остальные – лиственные.
Найти вероятность того, что среди трех отобранных деревьев:在树林中有60%是针叶类,其他是宽叶类,求选择3棵树,以下情况的概率:
А – все хвойные,全是针叶的
В – все лиственные,全是宽叶的
С – только 1 хвойное,只有1棵针叶
D – только 1 лиственное,只有1棵宽叶
Е – хотя бы 1 хвойное,至少1棵针叶
F – хотя бы 1 лиственное.至少1棵宽叶
|
| 2.7. В 17% кусков бисквита – по вишенке, в 34% других кусков - по изюминке. Три подруги взяли по кусочку бисквита. Найти вероятности, что подругам попались куски:蛋糕中17%是樱桃味,34%葡萄干的。取3块蛋糕,可能出现以下情况的概率:
А – всем без ягод,全部没有浆果
В – двум с вишенкой,两块樱桃的
С – хотя бы одной с ягодами,至少一块有浆果
D – двум с изюминами, а одной – с вишенкой,两块葡萄干的,一块樱桃的
Е – только одной с ягодами,只有一块浆果的
F – только одной с изюминой, остальным – без ягод.只有一块葡萄干的,其他没有浆果
| 2.8. Студент получает пятерку с вероятностью 40%, четверку – 50% и тройку с вероятностью 10%. Найти вероятность того, что студент получит в сессию из трех экзаменов:学生得五分概率是40%,四分50%,三分10%。求三科考试学生获得以下分数得概率:
А – только одну пятерку,只有1个五分
В – ровно 2 пятерки,正红2个五分
С – хотя бы две пятерки,至少2个五分
D – менее чем 2 пятерки,不到2个五分
Е – более чем 2 пятерки,超过2个五分
F – все пятерки.都是五分
|
| 2.09. 37,5% студентов кафедры проходили практику в фирмах, остальные – в госструктурах. Три друга одновременно принесли отчеты по практике. Найти вероятности, что они проходили практику:教研室37,5%的学生在公司实习,其他在国家机构。3个学生叫来实习报告。求他们实习出现以下情况的概率:
А – все в фирмах,都爱公司
В – все в госструктурах,都在国家机构
С – хотя бы 1 в госструктуре,至少1个在国家机构
D – хотя бы 1 в фирме,至少1个在公司
Е – не более двух в госструктурах,不超过2个在国家机构
F – только 1 в фирме.只有1个在公司
| 2.10. 50% полевых цветов желтого цвета, 30% – белого, остальные другой гаммы. Найти вероятность того, что среди двух взятых из букета цветов будет:野花中有50%是黄色的,30%是白色的,其他是别的颜色。求两束野花中以下情况的概率:
А – оба желтых,都是黄色
В – оба белых,都是白色
С – оба другой гаммы,都是其他颜色
D – хотя бы один желтый,至少一束黄色
Е – хотя бы 1 белый, 至少一束白色
F – нет желтых.没有黄色
|

 может произойти с вероятностью р или не произойти с вероятностью q = 1-p. Пусть опыт, в котором может появиться событие А 1
может произойти с вероятностью р или не произойти с вероятностью q = 1-p. Пусть опыт, в котором может появиться событие А 1  , повторяется два раза. Тогда, принимая во внимание правила умножения и сложения вероятностей, можно найти вероятности следующих событий: 让事件 А 1可能发生概率为 р 或者不会发生的概率为 q = 1-p 。进行事件 А 1的实验,重复两次。那么有以下概率加法与乘法的规则:
, повторяется два раза. Тогда, принимая во внимание правила умножения и сложения вероятностей, можно найти вероятности следующих событий: 让事件 А 1可能发生概率为 р 或者不会发生的概率为 q = 1-p 。进行事件 А 1的实验,重复两次。那么有以下概率加法与乘法的规则: не произойдет ни разу,
не произойдет ни разу,  ;一次都不发生,
;一次都不发生, ;只发生一次
;只发生一次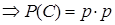 ;发生两次
;发生两次 . 至少发生一次,这是对立事件。
. 至少发生一次,这是对立事件。

 ;一次都不发生
;一次都不发生
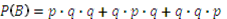 ;只发生一次
;只发生一次
 ;发生2次
;发生2次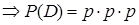 ;发生3次
;发生3次 ;至少发生2次,也就是说可能2次可能3次
;至少发生2次,也就是说可能2次可能3次 .至少发生1次,这是对立事件。
.至少发生1次,这是对立事件。
 или не произойти с вероятностью
или не произойти с вероятностью  . Независимо от этого событие
. Независимо от этого событие 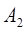 может произойти с вероятностью
может произойти с вероятностью 
 или не произойти с вероятностью
или не произойти с вероятностью  . Тогда, принимая во внимание правила умножения и сложения вероятностей, можно найти вероятности следующих событий:分析更复杂的情况。让事件
. Тогда, принимая во внимание правила умножения и сложения вероятностей, можно найти вероятности следующих событий:分析更复杂的情况。让事件  ;没有任何事件发生
;没有任何事件发生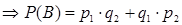 ;只有其中一种发生
;只有其中一种发生 ;两种同时发生
;两种同时发生 = 1 – 0,6 = 0,4 – вероятность не получить пятерки;
= 1 – 0,6 = 0,4 – вероятность не получить пятерки;  = 1 – 0,3 = 0,7 – вероятность не получить четверки;
= 1 – 0,3 = 0,7 – вероятность не получить четверки;  = 0,1 – вероятность получить тройку;
= 0,1 – вероятность получить тройку; 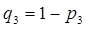 = 1 – 0,1 = 0,9 – вероятность не получить тройки.
= 1 – 0,1 = 0,9 – вероятность не получить тройки. ;
; = 0,432;
= 0,432;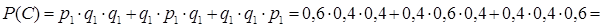 =0,288;
=0,288; ;
; ;
;
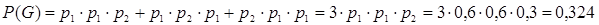 ;
; .
.


