Математическое ожидание – это среднее значение случайной величины, определяющее ее положение на числовой оси. Обозначается .

— СНК СССР принял постановление «О мероприятиях по увеличению производства товаров широкого потребления и продовольственных товаров пред приятиями местной промышленности, промысловой кооперации и кооперации инвалидов».

2 сентября — Подписание Акта о безоговорочной капитуляции Японии.

— Окончание второй мировой войны.

20 ноября (1945 г.) — 1 октября (1946 г.) — Нюрнбергский процесс над главными немецкими военными преступниками.

Оглавление

Введение ……………………………………………………………............
Основные определения …………………………………………………….
1. Выбор на основе классического определения вероятности.................
2. Сумма и произведение событий.........…………….................................
3. Формула полной вероятности и формула Байеса.................................
4. Ряд распределения дискретной случайной величины...........................
5. Числовые характеристики дискретной случайной величины...............
6. Биномиальное распределение (схема Бернулли).........………...............
7. Распределение Пуассона (закон редких событий)................................
8. Равномерное распределение...............…………….................................
9. Локальная и интегральная теоремы Лапласа........................................
10. Вариационный и статистический ряды.................................................
11. Группированный статистический ряд...................................................
12. Точечные оценки выборочных числовых характеристик…................
13. Точность и надежность оценки вероятности (формула Муавра-Лапласа)........................................................................................................
14. Проверка гипотез методом доверительных интервалов......................
15. Критерий Пирсона..................................................................................
16. Корреляционный анализ........................................................................
17. Корреляционный анализ при дихотомическом оценивании...............
18. Регрессионный анализ....................................................……................
Библиографический список.........................................................................
Приложения ………………………………………………………...............
Приложение 1. Значения функции Гаусса ………………….....................
Приложение 2. Значения функции Лапласа ……………...........................
Приложение 3. Критические точки распределения .............................

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ

基本概念

Событие называется случайным, если при неоднократном воспроизведении условий оно происходит каждый раз по-разному. Например, при подбрасывании монеты может выпасть картинка или цифра. Случайные события обозначаются прописными буквами А, В, С и т.д.

随机事件是指在反复重复的同样条件下，发生结果每次不一定不相同。例如，投掷硬币可能出现图案或数字。随机现象用字母A、B、C等表示。;

Вероятностью события А называется мера возможности его осуществления. Вероятность обозначается буквой р: Р(А), Р(В) и т.д.

事件的概率是衡量该事件发生的可能性的度量。概率用字母表示为 Р(А), Р(В)。;

За 1 принимается вероятность достоверного события, например вероятность выпадения или картинки или цифры при подбрасывании монеты. За 0 принимается вероятность невозможного события, например, выпадение двух картинок при подбрасывании монеты. Поэтому

1表示可能事件的概率，例如，投掷硬币时要么出现图案，要么出现数字，

0 表示不可能事件的概率，例如，投掷硬币时出现两个图案，

Значит, вероятность не может быть больше 1 или меньше 0.

也就是说，概率不可能大于1 或者小于0。

Случайной называется величина, которая при появлении случайного события принимает то или иное значение. Например, студент на экзамене может получить оценки «2», «3», «4» или «5» - это значения случайной величины «оценка на экзамене». Случайные величины обозначаются прописными буквами X, Y, Z и т.д. Значения случайных величин обозначаются строчными буквами x, y, z и т.д.

随机变量表示随机现象各种结果的实值。例如，学生在考试中可能得2、3、4、或5分— 这个考试成绩就是变量。我们一般用大写 X, Y, Z 表示随机变量，用小写 x, y, z 表示实数。;

Математическое ожидание – это среднее значение случайной величины, определяющее ее положение на числовой оси. Обозначается.

数学期望完全由随机变量的概率分布所确定，用 表示。

Дисперсия – это характеристика случайной величины, определяющая распределение ее значений относительно среднего. Обозначается. Следует заметить, что. Если, то величина Х не является случайной.

方差用来度量随机变量和其均值之间的偏离程度。用 表示，需要注意方差 ，如果 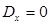，那么变量X就没有随机性。