Основы теории дискретных случайных величин
基本随机变量的理论; Закон распределения дискретной случайной величины Х имеет форму ряда распределения. Это таблица, связывающая все возможные значения случайной величины и вероятности, с которыми эти значения реализуются.随机变量的分布规律具有分布形式公式。下面表格,包括所有变量的数值与相应概率。
Вероятности реализации событий связаны соотношением所有这些概率合起来是1.
Графическое изображение ряда распределения называется полигоном распределения.图像绘制分布排列叫分布轨迹。 4.2. Пример решения типовых заданий по теме «Ряд распределения дискретной случайной величины» 例题详解; Задание № 4. Вариант 1. Коля, Петя и Сережа готовятся к экзамену по статистике. Коля может получить пятерку с вероятностью 90%, Петя – 70%, а Сережа – 20%. Построить ряд распределения и полигон числа пятерок, которые друзья могут получить на экзамене по статистике. Коля, Петя и Сережа三人准备统计考试,Коля可以获得5分的概率是90%, Петя 是70%, Сережа是20%。建立统计考试5分的分布规律与图像。 Решение. Прежде всего, определим форму ряда распределения случайной величины Х – числа пятерок, которые трое друзей могут получить на экзамене по статистике. Действительно, на троих они могут не получить ни одной пятерки, получить 1, 2 или 3 пятерки. Значит, ряд распределения в общем виде таков:首先决定三人获得5分的随机变量分布规律公式,当然三人可能获得不知一个,可能1个,2个,或者3个5分。
Осталось найти значения вероятностей Обозначим вероятности получения пятерки Колей Тогда вероятность не получить ни одной пятерки для трех друзей будет 三人1个5分都没有的概率
Событие «Получить 1 пятерку на троих» означает, что пятерку получит или Коля, или Петя, или Сережа, а остальные двое пятерок не получат. Вероятность этого события三人获得一个5分,意味着其中一人5分,另外两人没有5分,这个概率是
= 0,216 + 0,056 + 0,006 = 0,278. Аналогично вычисляется вероятность получения двух пятерок на троих
Вероятность получения пятерок всеми 3 друзьями равна
Найденные значения вероятностей позволяют завершить составление ряда распределения случайной величины Х, который принимает вид
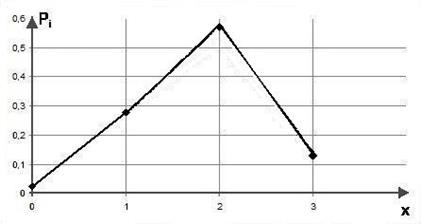
Очевидно, что 0,024 + 0,278 + + 0,572 + 0,126 = 1, т.е. выполняется соотношение (4.1) и построенный ряд распределения отвечает требованиям нормировки. Наиболее вероятным оказалось событие «Получить 2 пятерки на троих». Действительно, исходные значения вероятностей свидетельствуют в пользу того, что Петя и Коля, скорее всего, получат пятерки по статистике, а Сережа – нет. Как правило, результат математических вычислений в теории вероятностей подтверждает соображения житейской логики. Графический образ построенного ряда распределения – полигон.建立图像。 Для построения полигона по оси Х отложим в выбранном масштабе значения случайной величины: 0, 1, 2 и 3. На оси У найдем в другом масштабе соответствующие этим значениям вероятности: 0,024, 0,278, 0,572 и 0,126. Это будут соответственно абсциссы и ординаты узловых точек полигона. Построим эти узловые точки по заданным координатам. Соединив их отрезками прямых линий, получим требуемый чертеж полигона (рис. 4.1).
Рис. 4.1.Полигон числа пятерок, полученных друзьями
Задание № 4. Вариант 2. Компьютерный класс № 1 бывает занят в день 4 или 6 часов в зависимости от четной или нечетной учебной недели. Компьютерный класс № 2 используется для тестирования и бывает занят 3 часа в день в 90% случаев или 5 часов – в 10% случаев. Построить ряд распределения и полигон общего числа часов дневной занятости компьютерных классов. 计算机1号教室可能在单双周每天使用4个课时或者6个课时。计算机2号教室90%的时间每天使用3个课时,或者10%的时间每天使用5个课时。建立计算机教室使用随机变量分布规律和图像。 Решение. Пусть случайная величина Х – число часов в день, когда заняты оба компьютерных класса. Для построения ряда распределения Х сначала составим ряды распределения величин
Случайная величина Х может принимать значения, равные возможным суммам значений величин 随机变量X可以取不同的课时总数
Найдет значения вероятностей
Значение Х = 11 случайная величина принимает, если компьютерный класс № 1 работает 4 часа, а класс № 2 – 7 часов или компьютерный класс № 1 работает 6 часов, а класс № 2 – 5 часов:
Значение Х = 13 случайная величина принимает, если компьютерный класс № 1 работает 6 часов, а класс № 2 – 7 часов:
Ряд распределения случайной величины Х можно записать в виде
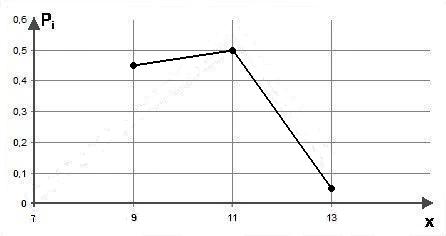
Очевидно, что 0,45 + 0,5 + + 0,05 = 1, и для построенного ряда выполнено соотношение нормировки (4.1).. Полигон распределения строится аналогично варианту 1 (рис. 4.2).
Рис. 4.2.Полигон числа часов дневной загрузки 4.3. Задания по теме «Ряд распределения дискретной
|

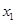

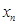
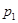
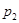
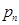
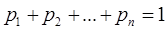 (4.1)
(4.1)

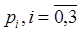 .
.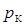 = 0,9, Петей
= 0,9, Петей 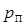 = 0,7, Сережей
= 0,7, Сережей 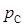 = 0,2. Соответственно, вероятность не получить пятерку для Коли
= 0,2. Соответственно, вероятность не получить пятерку для Коли 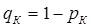 = 1 – 0,9 = 0,1, для Пети
= 1 – 0,9 = 0,1, для Пети 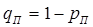 = 1 – 0,7 = 0,3, для Сережи
= 1 – 0,7 = 0,3, для Сережи 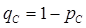 = 1 – 0,2 = 0,8.
= 1 – 0,2 = 0,8.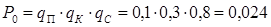 .
.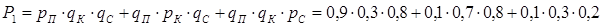
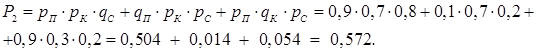
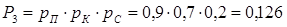 .
.
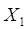 и
и 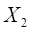 - числа часов занятости компьютерных классов № 1 и № 2 по отдельности.设随机变量X为每天两间教室的课时数量,先分别建立不同教师的随机变量分布规律。
- числа часов занятости компьютерных классов № 1 и № 2 по отдельности.设随机变量X为每天两间教室的课时数量,先分别建立不同教师的随机变量分布规律。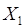
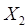
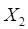 . Ряд распределения Х имеет вид
. Ряд распределения Х имеет вид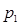 ,
, 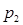 ,
, 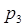 . Значение Х = 9 случайная величина принимает, если компьютерный класс № 1 работает 4 часа, а класс № 2 – 5 часов:
. Значение Х = 9 случайная величина принимает, если компьютерный класс № 1 работает 4 часа, а класс № 2 – 5 часов: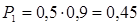 .
.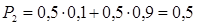 .
.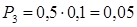 .
.