9.1. Основы применения теорем Лапласа для приближенного вычисления вероятностей событий при независимых испытаниях独立实验中使用拉普拉斯定理计算事件概率;
Если в схеме независимых испытаний Бернулли число опытов велико (десятки, сотни), то для подсчета вероятностей числа успехов можно пользоваться приближенными формулами, следующими из интегральной и локальной теорем Лапласа. То есть фактически дискретная случайная величина, распределенная по биномиальному закону, заменяется дискретным аналогом непрерывной случайной величины, распределенной по нормальному закону.
设在独立实验n序列中,事件A在各次实验中发生一种可能的概率为p,不发生的概率为q=1-p, 随机变量为X- 在n次试验中发生事件A的数量。
Пусть производится n независимых опытов. Событие А может появиться в одном опыте с вероятностью р, либо не появиться с вероятностью q = 1 – р. Случайная величина Х – число появлений события А в серии из n опытов.
Вероятность того, что случайная величина принимает определенное значение Х = m, можно найти с использованием локальной теоремы Лапласа:
 , (9.1)
, (9.1)
где 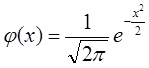 – функция Гаусса, значения которой сведены в таблицу в Приложении 1. Значение аргумента
– функция Гаусса, значения которой сведены в таблицу в Приложении 1. Значение аргумента  функции Гаусса вычисляется по формуле
функции Гаусса вычисляется по формуле
 . (9.2)
. (9.2)
Функция Гаусса обладает свойством четности  , поэтому в таблице Приложения 1 приведены ее значения только для положительных аргументов. Кроме того, эта функция – быстро убывает, поэтому для значений аргументов, больших 4 можно принимать
, поэтому в таблице Приложения 1 приведены ее значения только для положительных аргументов. Кроме того, эта функция – быстро убывает, поэтому для значений аргументов, больших 4 можно принимать  .
.
Поскольку число испытаний n велико, вероятность достичь появления события А определенное число раз достаточно мала. Кроме того, вероятность достижения непрерывно распределенной случайной величиной определенного значения теоретически равна 0. Эти обстоятельства делают формулу (9.1) мало применимой на практике. Практически значимые результаты дает формула вероятности попадания случайной величины на участок, следующая из интегральной теоремы Лапласа:
 , (9.3)
, (9.3)
где Ф(х) – нормированная функция Лапласа
 .
.
Лапласа сведены в таблицу в Приложении 2. Аргументы функции Лапласа 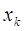 и
и  вычисляются по формуле (9.2).
вычисляются по формуле (9.2).
Функция Лапласа обладает свойством нечетности  , поэтому в таблице Приложения 2 приведены ее значения только для положительных аргументов. Кроме того, для значений аргументов, больших 5 можно полагать
, поэтому в таблице Приложения 2 приведены ее значения только для положительных аргументов. Кроме того, для значений аргументов, больших 5 можно полагать 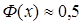 . Соответственно
. Соответственно
 . (9.4)
. (9.4)
9.2. Пример решения типового задания по теме «Локальная и интегральная теоремы Лапласа» 例题详解;
Задание № 9. 34% студентов не могут сдать экзамен по курсу «Статистика» с первого раза. Какова вероятность, что из 254 студентов смогли сдать экзамен с первого раза:有34%的学生不能第一次就通过统计考试,求出有254名学生第一次就能通过考试的概率:
1. 168 студентов,
2. от 150 до 170 студентов,
3. больше 160 студентов,
4. меньше 120 студентов.
Решение. Случайное событие А – студент сдал экзамен по статистике с первого раза. Случайная величина Х - число студентов, сдавших этот экзамен с первого раза. Определим значения параметров задачи: n = 254, q = 0,34, р = 1 – q = 1 – 0,34 = 0,66. Обратим внимание, что в задаче рассматриваются студенты, которые сдают экзамен с первого раза, т.е. в условии приведена вероятность противоположного события q. 随机事件A-学生第一次就能通过统计考试。随机变量X-第一次通过考试的学生数量。一次确定各参数值 n = 254, q = 0,34, р = 1 – q = 1 – 0,34 = 0,66.同时注意,因为该题是分析第一次通过考试的学生,所以该条件决定对立事件概率值 q。;
Найдем вероятность события Х = m = 168. Используем формулу (9.2):

По таблице Приложения 1 можем найти значение функции Гаусса только в ближайшей к  точке х = 0,05:
точке х = 0,05:  .
.
Значит  .
.
Найдем вероятности попадания случайной величины Х на интервалы. Используем формулу (9.3):
 .
.
Значения аргументов найдем по формуле (9.2):


По таблице Приложения 1 можем найти значение функции Лапласа:
 ,
,
 .
.
Тогда
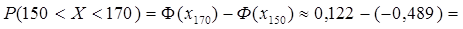
= 0,122 + 0,489 = 0,611.
Аналогично по формуле (9.3) находим оставшиеся вероятности, а аргументы функции Лапласа – по формуле (9.2):
 ,
,

Значение функции Лапласа находим по таблице Приложения 2:
 ,
, 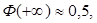
согласно соотношению (9.4).
Тогда
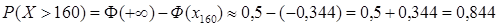 .
.
Аналогично:
 ,
,
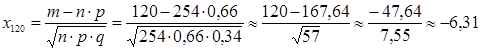 ,
,
 , т.к. 6,31 > 5,
, т.к. 6,31 > 5, 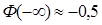 ,
,
согласно соотношению (9.4).
Тогда
 .
.
Полученные данные подтверждаются основными характеристиками нормального распределения. Действительно, четко выраженный максимум в точке математического ожидания  делает маловероятным, например, попадание значений случайной величины на полуинтервал
делает маловероятным, например, попадание значений случайной величины на полуинтервал  . Это следует и из известного «правила
. Это следует и из известного «правила  », которое утверждает, что попадание значений случайной величины за пределы интервала
», которое утверждает, что попадание значений случайной величины за пределы интервала  маловероятно. Проверим это утверждение.
маловероятно. Проверим это утверждение.
Найдем дисперсию случайной величины Х:
 .
.
Средне квадратическое отклонение
 .
.
Тогда  и
и  ,
,
 . Очевидно, что число 120 лежит за пределами интервала
. Очевидно, что число 120 лежит за пределами интервала  :
: 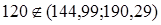 , т.е. маловероятно, практически невозможно, что случайная величина Х принимает значения, меньшие 120.
, т.е. маловероятно, практически невозможно, что случайная величина Х принимает значения, меньшие 120.
9.3. Задания по теме «Локальная и интегральные теоремы Лапласа»
习题;
| 9.1. 86% студентов опаздывают на лекции. Какова вероятность, что из 120 студентов на лекции опоздают:有86%的学生听讲座迟到,求120名学生中出现以下情况迟到的概率。
1. 90 студентов?90名学生
2. От 100 до 105 студентов?100到105名
3. Меньше 20 студентов?不到20名
4. Больше 80 студентов? 超过80名
| 9.2.26% туристов доходят до вершины. Какова вероятность, что из 245 туристов дойдут до вершины:有26%的游客可以登上山顶,求245名游客中出现以下情况登上山顶的概率。
1. 65 туристов?65名
2. От 50 до 60 туристов?50-60名
3. Меньше 70 туристов?不到70 名
4. Больше 120 туристов?超过120名
|
| 9.3. В магазине 17% просроченных консервов. Какова вероятность, что среди 378 банок консервов:商店中有17%的过期罐头。求378个罐头中出现以下情况的概率。
1. 62 просроченных?62个过期
2. От50 до70 просроченных?50-70个过期
3. Больше 65 просроченных?超过65个过期的
4. Меньше 100 просроченных?不到100个过期
| 9.4. 78% студентов списывают. Какова вероятность, что из 146 студентов 3-го курса:有78%的学生有抄袭情况,求3年级146名学生中出现以下情况的概率。
1. 115 списывают?115名抄袭
2. Меньше 70 списывают?不到70名
3. Больше 90 списывают?超过60名
4. От 100 до 120 списывают?100到120名
|
| 9.5. Только 24% туристов не имеют претензий к фирме «Слон». Какова вероятность, что из 235 туристов не имеют претензий:只有24%的游客对大象公司没有投诉,求在235名游客中出现以下没有投诉情况的概率
1. 60 туристов?60人
2. От 30 до 50 туристов?30-50人
3. Больше 120 туристов?超过120人
4. Меньше 40 туристов?不到40人
| 9.6. Только 17% опрошенных довольны своим заработком. Какова вероятность, что из 456 опрошенных довольны заработком:只有17%的人对自己的收入满意,求在456人中出现以下情况对自己收入满意的概率
1. 80 человек?80人
2. От 60 до 80 человек?60-80人
3. Больше 50 человек?超过50人
4. Меньше 40 человек?不到40人
|
| 9.7. В картинной галерее 68% картин низкого качества. Какова вероятность, что среди 125 картин: 在画廊有68%的质量较低,求在125幅油画中,出现以下情况低质量油画的概率。
1.85 низкого качества?85幅
2. От 80 до 100 низкого качества?80-100幅
3. Меньше 50 низкого качества?不到50幅
4. Больше 70 низкого качества?超过70幅
| 9.8. 28% детей наказывают лишением доступа к компьютеру. Какова вероятность, что из 326 наказанных детей лишены доступа к компьютеру:有28%的孩子受处罚时不允许玩电脑,求在326名儿童中出现以下处罚情况的概率。
1. 90 детей?90名
2. От 70 до 85 детей?70-85名
3. Меньше 100 детей?不到100名
4. Больше 200 детей?超过200名
|
| 9.9. 63% работников не хотят идти на пенсию. Какова вероятность, что среди 420 опрошенных работников пенсионного возраста не хотят идти на пенсию:有63%的工人不愿意退休,求在420名工人中出现以下不愿意退休情况的概率。
1. 250 человек?250人
2. От 240 до 260 человек?240-260人
3. Больше 150 человек?超过150人
| 9.10. 59% женщин любят сладкое. Какова вероятность, что из 218 сотрудниц фирмы любят сладкое:有59%的女性喜欢甜食,求218名公司员工中出现以下情况喜欢甜食的概率。
1. 130 сотрудницы?130人
2. От 115 до 120 сотрудниц?115到120人
3. Больше100 сотрудниц?超过100人
4. Меньше 150 сотрудниц?不到150人
|

 , (9.1)
, (9.1)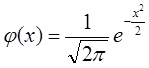 – функция Гаусса, значения которой сведены в таблицу в Приложении 1. Значение аргумента
– функция Гаусса, значения которой сведены в таблицу в Приложении 1. Значение аргумента  функции Гаусса вычисляется по формуле
функции Гаусса вычисляется по формуле . (9.2)
. (9.2) , поэтому в таблице Приложения 1 приведены ее значения только для положительных аргументов. Кроме того, эта функция – быстро убывает, поэтому для значений аргументов, больших 4 можно принимать
, поэтому в таблице Приложения 1 приведены ее значения только для положительных аргументов. Кроме того, эта функция – быстро убывает, поэтому для значений аргументов, больших 4 можно принимать  .
. , (9.3)
, (9.3) .
.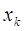 и
и  , поэтому в таблице Приложения 2 приведены ее значения только для положительных аргументов. Кроме того, для значений аргументов, больших 5 можно полагать
, поэтому в таблице Приложения 2 приведены ее значения только для положительных аргументов. Кроме того, для значений аргументов, больших 5 можно полагать 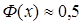 . Соответственно
. Соответственно . (9.4)
. (9.4)
 точке х = 0,05:
точке х = 0,05:  .
. .
. .
.

 ,
, .
.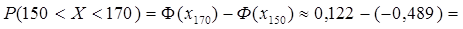
 ,
,
 ,
, 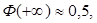
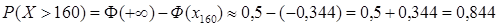 .
. ,
,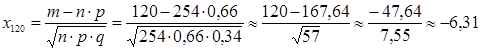 ,
, , т.к. 6,31 > 5,
, т.к. 6,31 > 5, 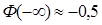 ,
, .
. делает маловероятным, например, попадание значений случайной величины на полуинтервал
делает маловероятным, например, попадание значений случайной величины на полуинтервал  . Это следует и из известного «правила
. Это следует и из известного «правила  », которое утверждает, что попадание значений случайной величины за пределы интервала
», которое утверждает, что попадание значений случайной величины за пределы интервала  маловероятно. Проверим это утверждение.
маловероятно. Проверим это утверждение. .
. .
. и
и  ,
, . Очевидно, что число 120 лежит за пределами интервала
. Очевидно, что число 120 лежит за пределами интервала  :
: 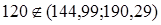 , т.е. маловероятно, практически невозможно, что случайная величина Х принимает значения, меньшие 120.
, т.е. маловероятно, практически невозможно, что случайная величина Х принимает значения, меньшие 120.


