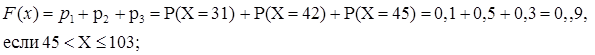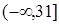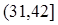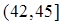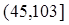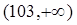ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
随机变量的数字特征 5.1. Основы теории числовых характеристик дискретной случайной величины 随机变量数字特征基本理论; Ряд распределения дискретной случайной величины (ДСВ) Х имеет вид:随机变量X(ДСВ)的分布
Вероятности реализации событий связаны соотношением (4.1):
Математическое ожидание ДСВ вычисляется по формуле
Дисперсия ДСВ вычисляется по формуле
Средне квадратическое отклонение (или просто отклонение) ДСВ вычисляется по формуле
Вероятность попадания ДСВ на участок равна сумме вероятностей, с которыми реализуются значения случайной величины, попадающие на этот участок.Такое вычисление вероятности возможно произвести, поскольку все значения, которые принимает случайная величина, попарно несовместны. Модой называется наиболее вероятное значение случайной величины. Значения функции распределения ДСВ Х находятся согласно следующему правилу
..............................
.
Можно построить таблицу значений функции распределения, имеющей постоянные значения на интервалах:
Графиком функции распределения, очевидно, является неубывающая ступенчатая функция, поскольку, согласно определению, все значения вероятности неотрицательны, а значит в нижнем ряду рассматриваемой таблицы суммируются с нарастанием неотрицательные величины. Такая функция иногда называется кусочно-постоянной. Ее вид можно посмотреть ниже для конкретных данных примера № 5 (рис. 5.2). 5.2. Пример решения типового задания по теме Задание № 5. Дан ряд распределения дискретной случайной величины. 给出随机变量分布规律
Найти求出 a, Mx, Dx, σх, Р (40<Х<50), Р (Х>35), Р (Х<150). Построить полигон, указать моду. Построить функцию распределения. 建立分布图像和函数分布。 Решение. Установим, что число значений ДСВ n = 4. Используя соотношение (5.1), получаем
Математическое ожидание находим по формуле(5.2),数学期望根据公式(5.2)可以求出
Дисперсию находим по формуле (5.3)
Средне квадратическое отклонение находим по формуле (5.4)
Такая величина отклонения, особенно при сопоставлении с математическим ожиданием на первый взгляд свидетельствует об определенном разбросе значений ДСВ, их недостаточной сгруппированности для того, чтобы в точных вероятностных моделях явлений, описываемых такой ДСВ, заменять эту величину ее средним по вероятности значением. Однако, с другой стороны, если рассмотреть оценку
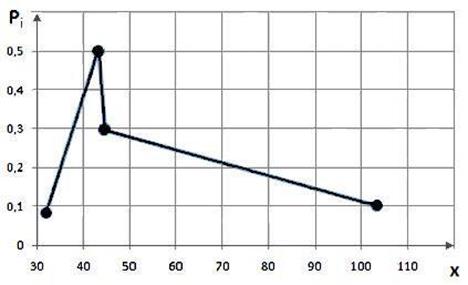
попадает 3 из 4 значений случайной величины, т.е. 75% ее значений, а это значит, что в приближенных вероятностных моделях вполне допустимо пользоваться математическим ожиданием данной ДСВ в качестве ее среднего значения, определяющего место ДСВ на числовой оси. Для построения полигона, как и в разделе 4, по оси Х отложим в выбранном масштабе значения случайной величины: 31, 42, 45 и 103. На оси У найдем в другом масштабе соответствующие этим значениям вероятности: 0,1, 0,5, 0,3 и 0,1. Это будут соответственно абсциссы и ординаты узловых точек полигона. Построим эти узловые точки по заданным координатам. Соединив узловые точки отрезками прямых линий, получим требуемый чертеж полигона (рис. 5.1).
Рис. 5.1.Полигон распределения ДСВ
Из рис. 5.1 видно, что наиболее вероятное значение ДСВ Х = 45, оно и будет модой распределения, т.е. mod = 45. Распределение является унимодальным, т.е. имеющим одну моду, причем ярко выраженную. Что, в свою очередь, подтверждает вывод: несмотря на относительно большой разброс, значения ДСВ достаточно сгруппированы относительного среднего – математического ожидания. Таким образом, математическое ожидание дает адекватное представление о месте рассматриваемой ДСВ на числовой оси. Действительно, 3 значения ДСВ – 31, 42 и 45 – сгруппированы вокруг математического ожидания 47,9. Единственное значение 103, разительно отличающееся и от остальных значений и от математического ожидания, ДСВ принимает с небольшой вероятностью 10%. Найдем вероятности попадания ДСВ на заданные участки. Р (40<Х<50) = Р(Х = 42) + Р(Х = 45) = 0,5 + 0,3 = 0,8, Р (Х>35) = Р(Х = 42) + Р(Х = 45) + Р(Х = 103) = 0,5 + 0,3 + 0,1 = 0,9, Р (Х<150) = Р(Х = 31) + Р(Х = 42) + Р(Х = 45) + Р(Х = 103) = = 0,1 + 0,5 + 0,3 + 0,1 = 1. Видно, что вероятность попадания ДСВ в сравнительно узкий интервал от 40 до 50 составляет 80%, что в очередной раз подтверждает факт сгруппированности значений ДСВ вокруг математического ожидания, которое со значением 47,9 попадает на тот же самый интервал. Функцию распределения ДСВ строим, используя правило (5.5):
. Таблица значений функции распределения имеет вид
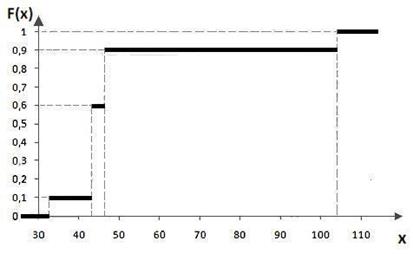
График этой ступенчатой функций изображен на рис. 5.2. Причем по обеим осям координат выбран подходящий масштаб, который обычно бывает различным, т.е. наиболее удобным и наглядным для каждой оси.
Рис. 5.2. Функция распределения ДСВ 5.3. Задания по теме «Числовые характеристики Текст задания. Дан ряд распределения дискретной случайной величины. Найти a, Mx, Dx, σх, Р (a <Х< b), Р (Х> c), Р (Х< d). Построить полигон, указать моду. Построить функцию распределения. Таблица 5.1 Варианты задания
|

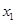

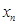
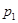
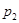
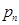
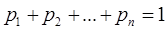 . (5.1)
. (5.1)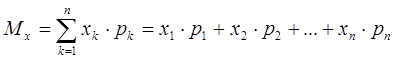 . (5.2)
. (5.2)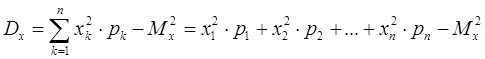 . (5.3)
. (5.3)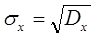 . (5.4)
. (5.4) ,
,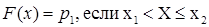 ,
, ,
, , (5.5)
, (5.5) ,
,
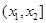
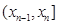

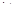
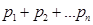
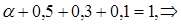
 .
.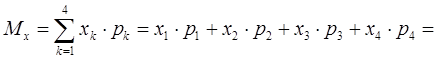
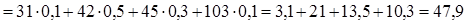 .
.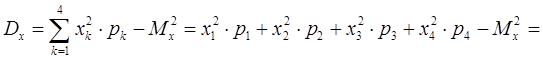
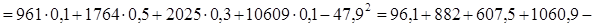
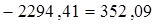 .
.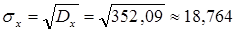 .
. , то можно заметить, что в интервал
, то можно заметить, что в интервал .
.
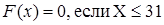 ,
,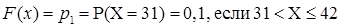 ,
,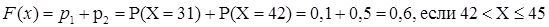 ,
,