全概率公式和贝叶斯公式
3.1. Основы экспертного оценивания 基本评估;
Пусть относительно наступления события А можно выдвинуть n попарно несовместных гипотез 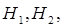 ...
... 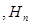 , априорные вероятности которых известны:
, априорные вероятности которых известны: 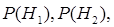 ...,
..., 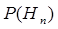 . Обычно предполагают, что гипотезы образуют полную группу, т.е. выполняется условие让事件A相对抽出n对不相容的假设为
. Обычно предполагают, что гипотезы образуют полную группу, т.е. выполняется условие让事件A相对抽出n对不相容的假设为 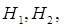 ...
... 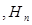 ,先期已知的概率为
,先期已知的概率为 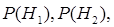 ...,
..., 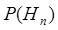 ,一般假定组成完整分组,满足下面条件:
,一般假定组成完整分组,满足下面条件:
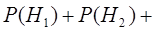 ...
... 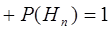 . (3.1)
. (3.1)
Событие А может наступить только вместе с одной из гипотез, причем известны условные вероятности наступления этого события 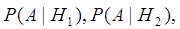 ...,
..., 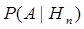 . Тогда вероятность наступления события А может быть вычислена по формуле полной вероятности:事件A发生出现一种假定的概率为
. Тогда вероятность наступления события А может быть вычислена по формуле полной вероятности:事件A发生出现一种假定的概率为 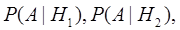 ...,
..., 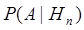 ,那么发生事件A的全概率可根据公式得出:
,那么发生事件A的全概率可根据公式得出:
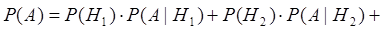 ...
...
+ 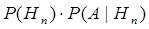 . (3.2)
. (3.2)
Пусть событие А произошло. Тогда можно переоценить вероятности гипотез, которые приводят к появлению этого события. Апостериорные вероятности гипотез вычисляются по формуле Байеса:让事件A发生,那么可以假定发生的概率。实际发生的概率可以根据贝叶斯公式求得:
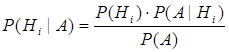 ,
, 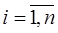 , (3.3)
, (3.3)
где 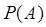 вычисляется по формуле полной вероятности (3.2).
вычисляется по формуле полной вероятности (3.2).
Если событие А не произошло, это означает, что произошло противоположное событие 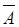 . Его вероятность
. Его вероятность 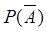 находится по формуле полной вероятности, аналогичной (3.2). При этом вероятности гипотез не меняются, а условные вероятности наступления события
находится по формуле полной вероятности, аналогичной (3.2). При этом вероятности гипотез не меняются, а условные вероятности наступления события 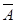 находятся по формуле вероятности противоположного события: 如果事件A没有发生,这意味着发生对立事件A,它的概率可根据全概率公式得到。这个情况下假定不发生变化,那么事件A发生的条件可根据对立事件公式得出:
находятся по формуле вероятности противоположного события: 如果事件A没有发生,这意味着发生对立事件A,它的概率可根据全概率公式得到。这个情况下假定不发生变化,那么事件A发生的条件可根据对立事件公式得出:
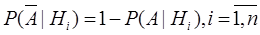 .
.
Апостериорные вероятности гипотез 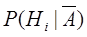 находятся по формуле Байеса, аналогичной (3.3).
находятся по формуле Байеса, аналогичной (3.3).
3.2. Пример решения типового задания по теме
«Формула полной вероятности и формула Байеса»例题解答;
Задание № 3. На курсе 120 студентов обучаются по направлению подготовки «Регионоведение», 70 – «Реклама». Абсолютная успеваемость студентов – регионоведов составляет 85%, студентов-рекламщиков – 55%. 《区域学》有120名学生,《广告学》有70名。顺利结束学业的学生《区域学》85%,《广告学》55%。
1. Какова вероятность, что случайно выбранный студент данного курса – успевающий?随机抽取到顺利结业学生的概率
2. Найти вероятность, что этот студент обучается по направлению подготовки «Реклама». 求抽取到《广告学》学生的概率
Решение. Событие А – выбранный студент успевающий. Выбранный студент может обучаться по одному из двух направлений подготовки, т.е. рассматриваем две гипотезы:事件A-顺利结业,所选学生可以学习其中一个方向,那么分析两种情况
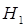 – студент обучается по направлению «Регионоведение»,学生学习《区域学》
– студент обучается по направлению «Регионоведение»,学生学习《区域学》
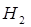 – студент обучается по направлению «Реклама».学生学习《广告学》
– студент обучается по направлению «Реклама».学生学习《广告学》
Тогда вероятности гипотез равны процентным долям студентов этих направлений относительно общего числа студентов курса. На курсе учится 120 + 70 = 190 студентов. Поэтому вероятности гипотез можно вычислить так:那么概率等于学习各专业方向除以总人数。总人数味190人,所以:
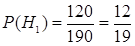 ,
,
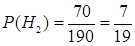 .
.
Заметим, что выполняется условие (3.1), что делает возможным впоследствии применять формулу Байеса. Действительно如果满足(3.1)的条件,就可以使用贝叶斯公式。
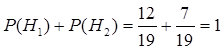 .
.
Вероятность того, что студент-регионовед успевает равна 85%, т.е.
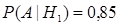 . Аналогично для студента-рекламщика
. Аналогично для студента-рекламщика 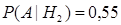 .
.
Тогда вероятность того, что выбранный студент успевающий, можно найти по формуле полной вероятности (3.2):所选顺利结业学生的概率,可以用全概率公式求得:
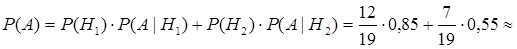
.
Значит, абсолютная успеваемость студентов курса составляет примерно 74%. 也就是说整个年级学生合格率为74%.
Найдем вероятность того, что выбранный случайным образом студент обучается по направлению «Реклама». Применяем формулу Байеса (3.3):求随机抽取的学习《区域学》的学生概率,可通过贝叶斯公式求得:
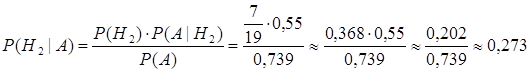 .
.
Вероятность составляет примерно 27%. Это немного, и вполне укладывается в представления житейской логики – действительно, и студентов-рекламщиков на курсе меньше и доля успевающих среди них ниже, чем среди регионоведов.概率大约是27%,这个概率不大,也是遵循逻辑可信的,那么年级中广告学学生更少,并且顺利结业的学生也更少。
3.3. Задания по теме «Формула полной вероятности
и формула Байеса» 习题;
| 3.1. В магазине марокканских мандаринов в 3 раза больше, чем турецких. Вероятность порчи марокканских мандаринов – 20%, а турецких – 35%.在商店中摩洛哥橘子是土耳其橘子的三倍,有20%的摩洛哥橘子坏掉,35%的土耳其橘子坏掉。
1. Найти вероятность, что случайно взятый мандарин – качественный.求拿到没坏掉的橘子的概率。
2. Какова вероятность, что этот мандарин – турецкий? 拿到土耳其橘子的概率。
| 3.2. В студенческой группе парней в 3 раза больше, чем девушек. Парни пропускают 50% занятий, а девушки – только 10%. 在班级中男生数量是女生的3倍,5男生出勤率50%,而女生只有10%。
1. Найти вероятность, что случайно выбранный при проверке студент отсутствует на занятии.求随机抽查时旷课学生的概率。
2. Какова вероятность, что это парень?抽查到男生的概率。
|
| 3.3. На диване 9 подушек, из них 3 жесткие. Вероятность спать со снами на мягкой подушке – 70%, на жесткой – 40%. Каждую ночь подушка выбирается случайно.在沙发上有9个枕头,其中有3个硬的。睡觉时睡软枕头做梦的概率时70%,硬枕头时40%。每个晚上选什么枕头时随机的。
1. Какова вероятность увидеть сон?求做梦的概率。
2. Какова вероятность, что при этом выбрали жесткую подушку?选到硬枕头的概率。
| 3.4. Вероятность увидеть ночью добрый или дурной сон равная. Вероятность запомнить добрый сон 75%, а дурной – 15%.晚上做噩梦和做美梦的概率是一样的。记住美梦的概率是75%,记住噩梦的概率是15%。
1. Какова вероятность запомнить сон?求记住梦的概率。
2. Найти вероятность, что при этом сон – добрый.求做美梦的概率。
|
| 3.5. В обменных группах в России 75% студентов из Финляндии, 20% из Германии и 5% из Китая. Финны заболевают в Санкт-Петербурге с вероятностью 5%, немцы – 50%, а китайцы – 60%. 在俄罗斯的交换学生中有75%来自芬兰,20%来自德国,5%来自中国。在圣彼得堡生活生病的概率是:芬兰学生5%,德国学生50%,中国学生60%。
1. Найти вероятность, что случайно выбранный студент, приехавший в Санкт-Петербург по обмену заболеет.求随机选取的生病学生的概率。
2. Какова вероятность, что это немец?选到德国学生的概率。
| 3.6. У бабушки 6 серых, 4 черных и 2 рыжих кота. Серые коты воруют мясо с вероятностью 20%, черные – 50%, а рыжие – 90%. Ночью один из котов случайно пробрался на кухню.奶奶有6只灰色的猫,4只黑色的,2只土黄色。灰色的有20%的概率偷肉,褐色的有50%的概率,土黄色有90%的概率。半夜有一只猫进了厨房。
1. С какой вероятностью мясо будет украдено?肉被偷的概率。
2. Какова вероятность, что это сделал черный кот?求肉被黑猫偷走的概率。
|
| 3.7. Фирма выполняет 5% крупных проектов, 40% средних и 55% мелких. Вероятность серьезных ошибок в мелком проекте 10%, в среднем – в 2 раза выше, а в крупном – в 4 раза выше.公司完成5%的大型项目,40%的中等项目,55%的小项目。小项目出现严重错误的概率是10%,中等项目高两倍,大型项目高四倍。
1. Найти вероятность, что в случайно проверенном проекте оказалась ошибка.求随机检查出错误的概率。
2. Какова вероятность, что это крупный проект?求随机抽到大型项目的概率。
| 3.8. В художественной галерее 20% картин XVIII века, 40% – XIX века, а остальные – XX века. Среди картин XVIII века 80% подделок, среди картин XIX века – 40%, а среди картин ХХ века – 5%. Купили 1 картину.在画廊有20%的油画是18世纪的,40%是19世纪的,其他事20世纪的。在18世纪油画中80%是赝品,19世纪中40%是赝品,20世纪中5%是赝品。随机买一幅油画。
1. Найти вероятность, что она подлинная.求买到真迹的概率。
2. Какова вероятность, что это оказалась картина XVIII века?求买到18世纪油画的概率。
|
| 3.9. В группе студентов программы «Международный семестр» 10 финнов, 5 немцев, 4 австрийца и 2 чеха. Финны пропускают занятия с вероятностью 70%, немцы – 15%, австрийцы – 20% и чехи – 40%.在国际交流学期项目班,有10名芬兰学生,5名德国学生,4名奥地利学生,2名捷克学生。芬兰学生旷课概率是70%,德国15%,奥地利20%,捷克40%。
1. С какой вероятностью случайно разыскиваемый студент пропустил занятия?随机抽到旷课学生的概率。
2. Какова вероятность, что это чех?求抽到旷课的是捷克学生的概率。
| 3.10. Преподаватель А спрашивает на экзамене в 3 раза больше студентов, чем В. При этом он ставит двойку с вероятностью 70%, а преподаватель В – с вероятностью 20%. 教师A在考试中提问的数量是教师B的3倍。教师A给不及格的概率是70%,教师B是20%。
1. С какой вероятностью случайно выбранный студент получит положительную оценку?随机抽到学生通过考试的概率。
2. Какова вероятность, что эту оценку поставил преподаватель А?随机抽到学生是由教师A通过考试的概率。
|

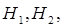 ...
... 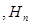 , априорные вероятности которых известны:
, априорные вероятности которых известны: 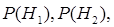 ...,
..., 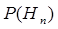 . Обычно предполагают, что гипотезы образуют полную группу, т.е. выполняется условие让事件A相对抽出n对不相容的假设为
. Обычно предполагают, что гипотезы образуют полную группу, т.е. выполняется условие让事件A相对抽出n对不相容的假设为 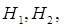 ...
... 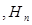 ,先期已知的概率为
,先期已知的概率为 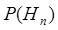 ,一般假定组成完整分组,满足下面条件:
,一般假定组成完整分组,满足下面条件: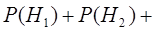 ...
... 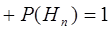 . (3.1)
. (3.1)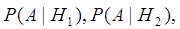 ...,
..., 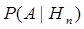 . Тогда вероятность наступления события А может быть вычислена по формуле полной вероятности:事件A发生出现一种假定的概率为
. Тогда вероятность наступления события А может быть вычислена по формуле полной вероятности:事件A发生出现一种假定的概率为 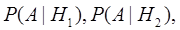 ...,
..., 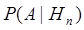 ,那么发生事件A的全概率可根据公式得出:
,那么发生事件A的全概率可根据公式得出: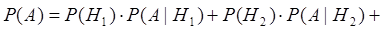 ...
...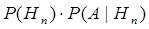 . (3.2)
. (3.2)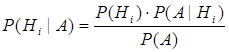 ,
, 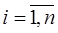 , (3.3)
, (3.3)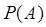 вычисляется по формуле полной вероятности (3.2).
вычисляется по формуле полной вероятности (3.2).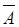 . Его вероятность
. Его вероятность 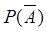 находится по формуле полной вероятности, аналогичной (3.2). При этом вероятности гипотез не меняются, а условные вероятности наступления события
находится по формуле полной вероятности, аналогичной (3.2). При этом вероятности гипотез не меняются, а условные вероятности наступления события 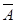 находятся по формуле вероятности противоположного события: 如果事件A没有发生,这意味着发生对立事件A,它的概率可根据全概率公式得到。这个情况下假定不发生变化,那么事件A发生的条件可根据对立事件公式得出:
находятся по формуле вероятности противоположного события: 如果事件A没有发生,这意味着发生对立事件A,它的概率可根据全概率公式得到。这个情况下假定不发生变化,那么事件A发生的条件可根据对立事件公式得出: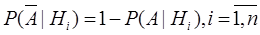 .
.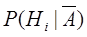 находятся по формуле Байеса, аналогичной (3.3).
находятся по формуле Байеса, аналогичной (3.3).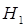 – студент обучается по направлению «Регионоведение»,学生学习《区域学》
– студент обучается по направлению «Регионоведение»,学生学习《区域学》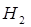 – студент обучается по направлению «Реклама».学生学习《广告学》
– студент обучается по направлению «Реклама».学生学习《广告学》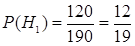 ,
,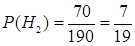 .
.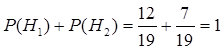 .
.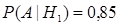 . Аналогично для студента-рекламщика
. Аналогично для студента-рекламщика 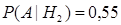 .
.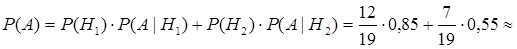
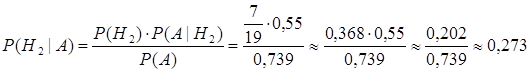 .
.


