БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
二项分布、伯努利实验 6.1. Основы теории биномиального распределения 二项分布基本理论; Пусть производится серия из n независимых опытов, в каждом из которых событие А может появиться с одинаковой вероятностью p, или не появиться с вероятностью q = 1 - p. Каждое появление или непоявление события А в любом из опытов серии не зависит от исхода других опытов этой же серии. Такая серия опытов называется схемой Бернулли. Случайная величина Х – это число появлений события А в серии из n опытов. Х – дискретная случайная величина, распределенная по биномиальному закону. Ряд распределения этой ДСВ Х имеет вид: 设重复进行n次实验,,实验结果只有发生或不发生两种可能,概率为p 和q,q=1-p,这一连串重复的独立实验为n重伯努利实验。X表示n重伯努利试验中A发生的次数,X 是一个随机变量,我们来求他的分布律。
Здесь
где
Вероятность того, что событие А появится от l до m раз в серии из n опытов можно найти по формуле
Математическое ожидание ДСВ, распределенной по биномиальному закону, вычисляется по формуле
Дисперсия ДСВ, распределенной по биномиальному закону, вычисляется по формуле
Полигон и функция распределения ДСВ, распределенной по биномиальному закону, строятся, как и для любой дискретной случайной величины, по правилам, описанным в разд. 5.
6.2. Пример решения типового задания по теме Задание № 6. Студент может получить пятерку на экзамене с вероятностью 60%. Найти ряд распределения числа пятерок, которые студент может получить в сессию из 3 экзаменов. Найти математическое ожидание и дисперсию числа пятерок, а также вероятность того, что их будет меньше 2. Построить полигон и функцию распределения.学生有60%的概率在考试时的5分,求学生参加3门考试获得5分的分布律。求数学希望值与方差,以及获得两个以下5分的概率。并绘制分布函数图像。 Решение. Случайная величина Х – число пятерок, которые студент может получить в сессию, очевидно, распределена по биномиальному закону.Действительно проводится ряд испытаний – экзаменов, в каждом из которых может появиться событие А – студент получает пятерку. Эти испытания по условиям задачи проводятся независимо, т.е. результат сдачи каждого из экзаменов не влияет на результат сдачи остальных, по крайней мере, в условиях задачи это не оговаривается. Значит, в нашем праве построить самую простую вероятностную модель изучаемого события – сдачи студентом сессии. В пользу нашего заключения свидетельствует один приведенный в условии факт – вероятность получения пятерки на каждом из экзаменов постоянна для данной сессии данного студента и равна p = 0,6. Соответственно q = 1 - p = 1 – 0,6 = 0,4. Здесь кроется источник главной идеализации, допускаемой при сведении задачи к схеме Бернулли. Действительно, любой, хоть немного знакомый с психологией, либо умудренный пусть и небольшим житейским опытом, понимает, что получение или не получение пятерки уже на первом экзамене, скорее всего, то есть с большой долей вероятности, повлияет на результаты сдачи студентом остальных экзаменов. Как оно повлияет – неясно. Действительно, студент, получив пятерку на первом экзамене, может почувствовать себя окрыленным и «влёт» сдать остальные, а может, наоборот, расслабиться... Для построения более точных вероятностных моделей необходимы серьезные исследования в области педагогической психологии, обработка больших объемов статистических данных и т.д. Ясно, что при решении задач, дающих ответы на глобальные вызовы современности, так и должно происходить. В простых же случаях, подобных нашему, вполне уместна и упрощенная схема Бернулли. Поскольку наибольшее число пятерок, которые студент может получить в сессию равно 3, то n = 3, и ряд распределения ДСВ имеет вид 随机变量X是学生的5分的数量,学生获得5分是实验A,这个满足重伯努利实验定律,每一次实验室独立的,每次获得的成绩不影响其他考试的成绩,那么得5分的概率 p = 0,6. 相反不得五分的概率 q = 1 - p = 1 – 0,6 = 0,4。有三门考试,所以最多有3个5分,所以 n=3, 一次建立随机变量分布
Чтобы получить конкретный вид ряда распределения, найдем вероятности
где биномиальные коэффициенты
Полигон строится способом, подробно описанным в разд. 4 и 5. Его график приведен на рис. 6.1. Четко выделяется мода распределения, равная 2: mod = 2. 图像建立方法在4和5部分详细分析。在图6.1 中建立图像。清晰可辨众数的分布
Рис. 6.1. Полигон числа пятерок, полученных 学生在考试中的成绩图像 Математическое ожидание и дисперсия случайной величины Х, распределенной по биномиальному закону, находятся по формулам (6.4) и (6.5) 数学期望与随机变量X的方差,根据根据公式(6.4) и (6.5)如下
Вероятность того, что студент получит не меньше 2 пятерок в сессию, означает вероятность, что он может получить 2 или 3 пятерки, которая вычисляется по формуле (6.3): 学生在会话考试中获得不少于2个五分的概率由下式计算出
Эта вероятность оказывается более 50%, поскольку события, состоящие в получении 2 или 3 пятерок, являются наиболее вероятными во всем ряде распределения. 这个概率显示出50%以上,根据事实,取得两个或三个五分具有最大的可能性 Для построения функции распределения величины Х, распределенной по биномиальному закону, воспользуемся правилом (5.5): 为了构造X的分布函数,根据二项式分布规律,我们使用:
Таблица значений функции распределения имеет вид函数的值分布的表格形式
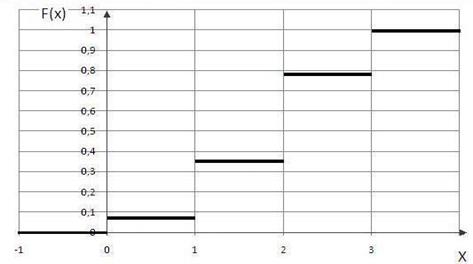
График этой ступенчатой функций изображен на рис. 6.2. Причем по обеим осям координат выбран различный, способствующий наглядности изображения, масштаб. 根据不同的比例在两轴上建立了该阶梯函数的曲线,示于图6.2 。
Рис. 6.2. Функция распределения биномиального
6.3. Задания по теме «Биномиальное распределение» 习题;
7. РАСПРЕДЕЛЕНИЕ ПУАССОНА
|



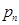
 , т.е. представляет собой вероятность того, что событие А появится ровно k раз в серии из n опытов. Эти вероятности вычисляются по формуле Бернулли:
, т.е. представляет собой вероятность того, что событие А появится ровно k раз в серии из n опытов. Эти вероятности вычисляются по формуле Бернулли: , (6.1)
, (6.1) – биномиальный коэффициент, или число сочетаний из n элементов по k, которое находится по формуле (1.2):
– биномиальный коэффициент, или число сочетаний из n элементов по k, которое находится по формуле (1.2): . (6.2)
. (6.2) . (6.3)
. (6.3) . (6.4)
. (6.4) . (6.5)
. (6.5)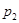

 по формулам Бернулли (6.1): 伯努利概率公式(6.1)
по формулам Бернулли (6.1): 伯努利概率公式(6.1)



 найдены по формуле (1.2) с учетом соотношений (1.3). 其中二项式系数
найдены по формуле (1.2) с учетом соотношений (1.3). 其中二项式系数 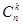 由公式(1.2)求出,并考虑上述关系( 1.3)Тогда ряд распределения ДСВ принимает вид那么该系列随机分布变量分布的形式
由公式(1.2)求出,并考虑上述关系( 1.3)Тогда ряд распределения ДСВ принимает вид那么该系列随机分布变量分布的形式
 ,
, .
. .
.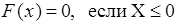 ,
, ,
, ,
,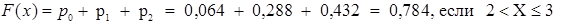 ,
, .
.