Основы выбора на базе классического определения вероятности
Пусть имеется n элементов, различающихся свойствами или качествами. Причем среди них r элементов одного типа, l элементов другого типа и т.д., q элементов последнего типа, так что выполняется условие 设有 n 个元素,具有不同性质,在其中有 r 个元素是同一类型, l 个元素是另一类型,以此类推, q 个元素是最后一类,那么满足条件 n = r + l + … + q. Случайным образом отбирают m элементов, причем порядок выбора не важен, важен только состав отобранной группы элементов. Вероятность того, что в отобранной группе оказалось k элементов первого типа, j элементов второго типа и т. д., i элементов последнего типа, так чтобы 设随机选择 m 个元素,选择顺序不重要,但选择元素分类重要。那么概率为,第一类 k 个元素,第二类 j 个元素,以此类推,最后一类 i 个元素,那么 m = k + j + … + i, вычисляется по формуле根据公式计算
где其中
Полезно знать и уметь использовать следующие свойства сочетаний: 了解并使用下列属性的组合: 1. 2. 3.
1.2. Решение типового задания по теме «Выбор на основе Задание № 1. В академической группе 10 студентов проживают в Санкт-Петербурге, 7 приехали из других городов России и 3 иностранца. На прием в деканат пришли 5 студентов из этой группы. Найти вероятности событий:在班级中有10名学生住在圣彼得堡,7名来自俄罗斯其他城市,有3名外国学生。在系主任接待时间到来5名学生。求事件概率: А. Все – из Санкт-Петербурга.全部来自圣彼得堡 В. 2 – из других городов России и 3 иностранца.2名来自俄罗斯其他城市,3名外国学生 С. 3 – из Санкт-Петербурга, 1 – из другого города России и 1 иностранец. 3名来自圣彼得堡,1名来自俄罗斯其他城市,1名外国学生 D. Все иностранцы пришли на прием.外国学生都来了 Решение. Поскольку порядок выбора не важен в условиях задачи, то пользуемся формулой (1.1).解题时选择顺序不重要,那么根据公式 Определим значения параметров: n = 20, m = 5, r = 10, l = 7, q = 3. Найдем Р(А). Изобразим графически схему выбора. В левом блоке – общее число участников выбора (20) и их распределение по трем категориям – жители Петербурга, другие россияне и иностранцы (10 + 7 + 3). Стрелки означают выбор. Стрелка слева направо показывает выбор общего числа, вне зависимости от категорий. Стрелки сверху вниз указывают на конкретный выбор из каждой категории. 求概率 Р(А)。; 绘制选择图像,左侧总数20,分为3类,彼得堡、俄罗斯其他城市、外国学生(10+7+3),剪头代表选择,右指剪头表示选择总数,下指剪头表示分类。
Тогда параметрызадачи принимают значения: k = 5, j = i = 0 . Тогда
Вычислим
В соответствии со свойствами сочетаний Тогда
Найдем Р(В). Изобразим графически схему выбора求概率 Р(В) 可同上绘制选择图像
Тогда параметрызадачи принимают значения: k = 0, j = 2, i = 3 . Тогда
Вычислим
В соответствии со свойствами сочетаний
Тогда
Найдем Р(С). Изобразим графически схему выбора求概率 Р(C) 可同上绘制选择图像
Тогда параметрызадачи принимают значения: k = 3, j = 1, i = 1 .
Тогда
Вычислим
В соответствии со свойствами сочетаний Тогда
Вычисленные вероятности событий А, В и С вполне подтверждаются обыденной логикой. Например, студенты из Санкт-Петербурга составляют половину всей академической группы и не встретить их около деканата среди других студентов этой группы – маловероятное событие. Действительно, вероятность события В – наименьшая из всех вычисленных, в частности она приблизительно в 160 раз меньше ближайшей к ней по значению вероятности события С. 求事件A、B、C发生的概率有相应的逻辑性。例如,极小可能发生:全部圣彼得堡学生都在系主任接待时间集合而不会遇到其他学生。而发生B的可能性更小,发生C的概率是B的几乎160倍。 Для того, чтобы найти Р(D), необходимо изменить схему выбора. Действительно, на прием в деканат пришли все иностранцы, т.е. 3 из 3. Для ответа на вопрос задачи не важно, какие именно 2 других студента пришли на прием. То есть выбор производится из двух категорий: «иностранцы» и «не иностранцы». 要求得概率D,需要改变绘制图像的结构,当然3明外国学生全部都到,那么就只在两类中选择:外国学生和非外国学生。Поэтому исходные параметры таковы: 所以 n = 20, m = 5, r = 3, l = 17 (количество «не иностранцев» l = 20 – 3 = 17). Графическая схема выбора такова:
Тогда параметрызадачи принимают значения: k = 3, j = 2 .
Тогда
Вычислим
В соответствии со свойствами сочетаний Тогда
Действительно, выбор всей малочисленной категории с математической точки зрения маловероятен, что и демонстрирует значение вероятности события D. 从数学的角度发生D的可能性最小。 1.3. Задания по теме «Выбор на основе классического
|

 , (1.1)
, (1.1) ‑ число сочетаний из n элементов по m:
‑ число сочетаний из n элементов по m: . (1.2)
. (1.2)
 (1.3)
(1.3) .
. 20
20
 10
10
 7
7
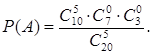


 .
.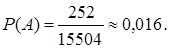


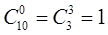 .
.
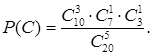

 .
.
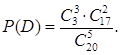

 .
.



