Степени корреляции
Эта классификация не является общепризнанной, но вполне пригодна для использования. Другие источники именуют существенную степень корреляционной связи средней или умеренной, сильную – высокой. Принадлежность пограничных значений (кроме 0 и 1) к определенной градации степени корреляции также разнится среди источников. Кроме того, при Следует отметить, что полный вывод об отсутствии или наличии корреляционной связи между величинами и ее степени можно сделать лишь на основании проверки соответствующей гипотезы, принимающей во внимание объем двумерной выборки.
16.2. Пример решения типового задания по теме Задание № 16. Найти коэффициент корреляции по двумерной выборке и сделать вывод о наличии корреляционной связи между Х и У и ее степени.
Решение. Найдем выборочные средние по формулам (16.1) и (16.2):
Найдем выборочные дисперсии по формулам (16.3) и (16.4):
Найдем выборочные отклонения по формулам (16.5) и (16.6):
Внимание: рекомендуется вычислять выборочные отклонения с точностью, по крайней мере, до третьего знака включительно. Это связано с необходимостью обеспечить высокую точность вычисления коэффициента корреляции при его значениях, близких к 1 (или к 0). Найдем выборочный корреляционный момент по формуле (16.7):
Найдем выборочный коэффициент корреляции по формуле (16.8):
Вывод: между случайными величинами Х и У наблюдается сильная отрицательная корреляционная связь. Еще раз повторим, что окончательное заключение можно сделать лишь на основании проверки гипотезы о наличии корреляционной связи, принимая во внимание объем двумерной выборки. 16.3. Задания по теме «Корреляционный анализ» Текст задания. Найти выборочный коэффициент корреляции по двумерной выборке и сделать вывод о наличии корреляционной связи между Х и У и ее степени. Таблица 16.2 Варианты задания
|
÷ 0,3)
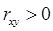корреляционная связь называется положительной или прямой, при 
– отрицательной или обратной.
;
.
;
.
, 
.
.
.
