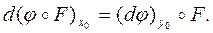Нехай М — множина в  .
.
За допомогою операції над формами в точці очевидним чином визначаємо додавання і добуток диференціальних форм на множині М:
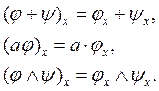
При такому означенні диференціальні р-форми на М створюють векторний простір.
Якщо кожній точці х 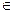 М ми поставимо у відповідність диференціальну р-форму
М ми поставимо у відповідність диференціальну р-форму
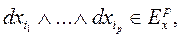
то ми отримаємо деяку визначену диференціальну форму на множині М, яку ми знову будемо позначати символом  . Всяку диференціальну форму
. Всяку диференціальну форму  порядку р можна единим чином записати в канонічному вигляді
порядку р можна единим чином записати в канонічному вигляді
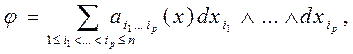
де 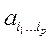 —деякі дійсні функції, визначені на множині М. Тому розумно слідуюче
—деякі дійсні функції, визначені на множині М. Тому розумно слідуюче
Означення 4.2. Диференціальна р-форма  на множині М називається неперервною в точці х
на множині М називається неперервною в точці х 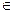 М, якщо коефіцієнти форми
М, якщо коефіцієнти форми  , записаної в канонічному вигляді, неперервні в точці х0. Якщо множина М допустима, то форма
, записаної в канонічному вигляді, неперервні в точці х0. Якщо множина М допустима, то форма  називається диференційованою (відповідно неперервно диференційованою, n раз неперервно диференційованою, незкінченно диференційованою), якщо цією властивістю володіють функції
називається диференційованою (відповідно неперервно диференційованою, n раз неперервно диференційованою, незкінченно диференційованою), якщо цією властивістю володіють функції  .
.
На векторних просторах диференційовних р-форм вводять диференціальний оператор, що являє собою узагальнення поняття повного диференціала функції. Нагадаємо спочатку це останє поняття.
Якщо функція f диференційована в точці х0 і  , то умова
, то умова
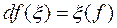
визначає деяку пфаффову форму 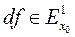 — повний диференціал функції
— повний диференціал функції 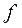 . Справедливе правило Лейбніца
. Справедливе правило Лейбніца

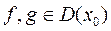
Ось канонічний вигляд форми 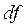 :
:
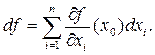
Якщо функція 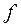 диференційована в кожній точці множини М, то
диференційована в кожній точці множини М, то 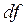 являється диференціальною 1-формою на множині М. Тепер ми дамо
являється диференціальною 1-формою на множині М. Тепер ми дамо
Означення 4.3. Нехай
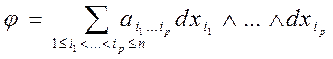
— деяка р-форма, визначена на допустимій множині М і диференційована в точці х0 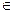 М. Під зовнішнім диференціалом форми
М. Під зовнішнім диференціалом форми  в точці х0 розуміють диференціальну форму порядку р+1
в точці х0 розуміють диференціальну форму порядку р+1
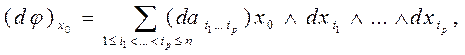
визначену в точці х0.
Форму 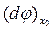 називають також зовнішньою похідною форми
називають також зовнішньою похідною форми  . По більшій мірі ми будемо писати скорочено:
. По більшій мірі ми будемо писати скорочено:  . Таким чином,
. Таким чином,
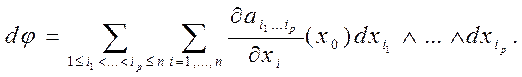
Якщо форма  диференційована на всій множині М, то відповідність
диференційована на всій множині М, то відповідність 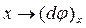 є визначеною на множині М (р+1)-формою
є визначеною на множині М (р+1)-формою  . Очевидно,
. Очевидно, 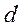 являється R-лінійним оператором:
являється R-лінійним оператором:
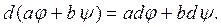
Теорема 4.1. Якщо  і
і  — диференціальні форми відповідно поряду р і q, визначені на допустимій множині М і диференційовані в точці х0
— диференціальні форми відповідно поряду р і q, визначені на допустимій множині М і диференційовані в точці х0 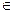 М, то
М, то
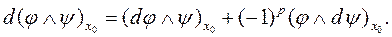

Теорема 4.2 Нехай f – функція, диференційована на компактному кубі М з ребрами, паралельними осям координат, і двічі диференційована в точці х0 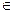 М. Тоді
М. Тоді 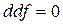 в точці х0.
в точці х0.
Теорема 4.3. Нехай  - диференціальна форма, диференційована на компактному кубі М з ребрами, паралельними осям координат, і двічі диференційована в точці х0
- диференціальна форма, диференційована на компактному кубі М з ребрами, паралельними осям координат, і двічі диференційована в точці х0 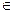 М, то в цій точці
М, то в цій точці 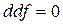 .
.
Введемо слідуючу термінологію:
Означення 4.4. Диференційована (в точці х0) диференціальна форма  називається замкнутою (в точці х0), якщо
називається замкнутою (в точці х0), якщо 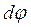 =0 (відповідно
=0 (відповідно 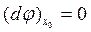 ). Диференційовна форма
). Диференційовна форма  називається точною (в точці х0), якщо існує диференційована (в точці х0) диференціальна форма
називається точною (в точці х0), якщо існує диференційована (в точці х0) диференціальна форма  , для якої
, для якої 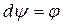 (відповідно
(відповідно 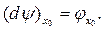 ).
).
Із теореми 4.3 випливає
Теорема 4.4. Якщо диференціальна форма  на відкритій множині М являється точною, то вона замкнута.
на відкритій множині М являється точною, то вона замкнута.
На закінчення розглянемо ще поведінку диференціальних форм і зовнішнього диференціала при диференційованих відображеннях. Нехай М — допустима множина в 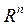 і
і  —довільна множина. Нехай, далі,
—довільна множина. Нехай, далі, 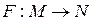 диференційовне відображення. Якщо відображення
диференційовне відображення. Якщо відображення 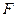 задається функціями
задається функціями  і
і
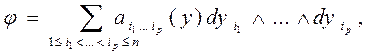
- деяка диференціальна форма порядку р на множині 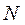 , то умова
, то умова
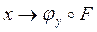 (де у=
(де у= 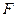 (х))
(х))
визначає на множині М диференціальну р-форму 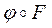 , яка може бути записана у вигляді
, яка може бути записана у вигляді
 .
.
Якщо відображення F нескінченно диференційоване і множина N допустима, то форма 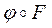 володіє тими ж властивостями диференційованості, що і форма
володіє тими ж властивостями диференційованості, що і форма  . Має місце
. Має місце
Теорема 4.5. Нехай форма  диференційована в точці
диференційована в точці 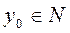 (множина N повинна бути допустимою), і нехай відображення Р двічі диференційоване в точці х0, для якої
(множина N повинна бути допустимою), і нехай відображення Р двічі диференційоване в точці х0, для якої 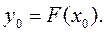 .Нехай, крім того, існує такий компактний куб U з ребрами, паралельними осям координат, що х0. Тоді
.Нехай, крім того, існує такий компактний куб U з ребрами, паралельними осям координат, що х0. Тоді
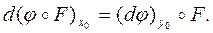

 .
.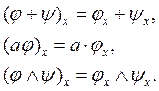
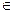 М ми поставимо у відповідність диференціальну р-форму
М ми поставимо у відповідність диференціальну р-форму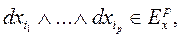
 . Всяку диференціальну форму
. Всяку диференціальну форму  порядку р можна единим чином записати в канонічному вигляді
порядку р можна единим чином записати в канонічному вигляді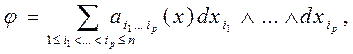
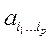 —деякі дійсні функції, визначені на множині М. Тому розумно слідуюче
—деякі дійсні функції, визначені на множині М. Тому розумно слідуюче .
. , то умова
, то умова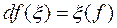
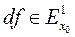 — повний диференціал функції
— повний диференціал функції 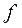 . Справедливе правило Лейбніца
. Справедливе правило Лейбніца
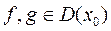
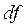 :
: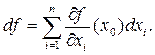
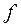 диференційована в кожній точці множини М, то
диференційована в кожній точці множини М, то 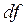 являється диференціальною 1-формою на множині М. Тепер ми дамо
являється диференціальною 1-формою на множині М. Тепер ми дамо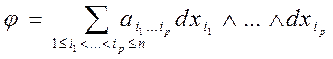
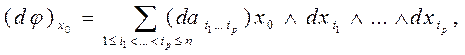
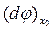 називають також зовнішньою похідною форми
називають також зовнішньою похідною форми  . Таким чином,
. Таким чином,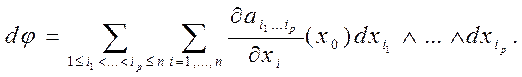
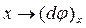 є визначеною на множині М (р+1)-формою
є визначеною на множині М (р+1)-формою 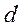 являється R-лінійним оператором:
являється R-лінійним оператором: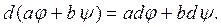
 — диференціальні форми відповідно поряду р і q, визначені на допустимій множині М і диференційовані в точці х0
— диференціальні форми відповідно поряду р і q, визначені на допустимій множині М і диференційовані в точці х0 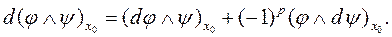

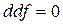 в точці х0.
в точці х0. називається замкнутою (в точці х0), якщо
називається замкнутою (в точці х0), якщо 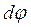 =0 (відповідно
=0 (відповідно 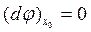 ). Диференційовна форма
). Диференційовна форма 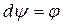 (відповідно
(відповідно 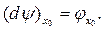 ).
).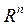 і
і  —довільна множина. Нехай, далі,
—довільна множина. Нехай, далі, 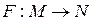 диференційовне відображення. Якщо відображення
диференційовне відображення. Якщо відображення 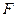 задається функціями
задається функціями  і
і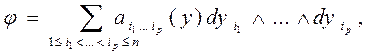
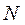 , то умова
, то умова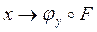 (де у=
(де у= 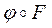 , яка може бути записана у вигляді
, яка може бути записана у вигляді .
.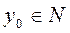 (множина N повинна бути допустимою), і нехай відображення Р двічі диференційоване в точці х0, для якої
(множина N повинна бути допустимою), і нехай відображення Р двічі диференційоване в точці х0, для якої 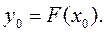 .Нехай, крім того, існує такий компактний куб U з ребрами, паралельними осям координат, що х0. Тоді
.Нехай, крім того, існує такий компактний куб U з ребрами, паралельними осям координат, що х0. Тоді