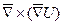Умова потенційності поля
В якості визначення потенційного поля зазвичай приймають одне із таких властивостей: 1. Робота залежить тільки від початкової і кінцевої точки шляху і не залежить від траєкторії руху; 2. Силове поле є градієнтом деякої скалярної функції (потенціалу), тобто
Безпосередня перевірка цих умов була б надзвичайно складна. Спираючись на властивості криволінійних інтегралів можна показати, що друга умова є наслідком першої. Покажемо, що достатньою умовою потенційності поля є рівність його ротора нулю. Припустимо, що в деякій області rot Розглянемо роботу, виконувану при переміщенні по траєкторіях APB і AQB (див. малюнок 7). Робота, як відома, може бути обчислена криволінійним інтегралом другого роду по траєкторії руху. Розглянемо різницю роботи на траєкторіях APB і AQB: A1 - A2 = бо при зміні напрямку руху на протилежний робота змінює знак. Враховуючи властивість адитивності інтегралів, отримуємо, що A1 - A2 =
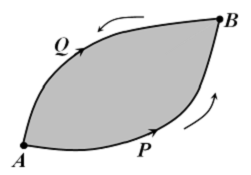
Нехай S поверхня, границя якої є замкнутим контуром APBQA. Застосуємо формулу Стокса: A1 - A2 = Таким чином для векторного поля з нульовим ротором робота не залежить від шляху. Легко переконатися, що рівність нулю ротора є також і необхідною умовою потенційності поля. Припустимо, що формально являє собою векторний добуток векторів, що відрізняються тільки скалярним множником, і дорівнює нулю. Для звичайних векторів це відповідає тому факту, що векторний добуток колінеарних векторів дорівнює нулю. Вектор «Набла» ніякого напряму, зрозуміло, не задає. Однак, істинність результату можна встановити безпосереднім обчисленням:
Пояснимо останню рівність. Якщо всі компоненти векторного поля мають безперервні частинні похідні, то умови теореми про перестановку порядку диференціювання виконані. Змішані похідні функції U, що відрізняються лише порядком диференціювання, збігаються. Відтак всі дужки в останньому виразі тотожно дорівнюють нулю. Отже, необхідною і достатньою умовою (критерієм) потенційності векторного поля, є тотожна рівність нулю його ротора. Доведення цього факту, як було показано вище, спирається на формулу Стокса.
|

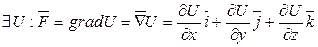 .
. виконується умова
виконується умова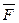 =
= 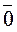 .
.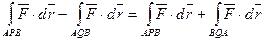 ,
,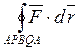 .
.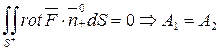 .
.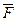 = grad U. У цьому випадку ротор векторного поля rot
= grad U. У цьому випадку ротор векторного поля rot