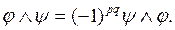Перш за все введемо поняття дотичного простору. Нехай 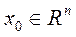 . Позначимо через
. Позначимо через 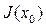 множину всіх функцій f,визначених в деякому (залежному від f) околі U точки
множину всіх функцій f,визначених в деякому (залежному від f) околі U точки  і неперервних в точці
і неперервних в точці  . А через
. А через  множину тих функцій
множину тих функцій  , які, крім того, диференційовані в точці
, які, крім того, диференційовані в точці  . В просторах
. В просторах 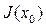 і
і  визначені слідуючі операції: додавання, добутку і добутку на дійсне число. Із
визначені слідуючі операції: додавання, добутку і добутку на дійсне число. Із  ,
,  і
і  випливає, що
випливає, що  . Дотичним вектором в точці
. Дотичним вектором в точці  називається лінійне відображення
називається лінійне відображення  , що володіє слідуючими додатковими властивостями:
, що володіє слідуючими додатковими властивостями:
а) 
б) якщо  ,
,  і
і  , то
, то  ;
;
в) 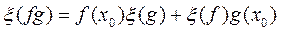 при
при  .
.
Дотичні вектори в точці  утворюють n-вимірний векторний простір
утворюють n-вимірний векторний простір  , який утворюється частинними похідними
, який утворюється частинними похідними  , v= 1 ,…,n. При цьому
, v= 1 ,…,n. При цьому  - це дотичний вектор, що визначається умовою
- це дотичний вектор, що визначається умовою  . Простір
. Простір  називається дотичним простором в точці
називається дотичним простором в точці  .
.
Означення 2.1. Зовнішні р-лінійні форми в дотичному просторі  називаються (зовнішніми) диференціальними формами порядку р в точці
називаються (зовнішніми) диференціальними формами порядку р в точці  (або, короче, зовнішніми р-формами).
(або, короче, зовнішніми р-формами).
Е1 =  є векторним простором пфаффовых форм в точці х0. Цей простір створюється формами
є векторним простором пфаффовых форм в точці х0. Цей простір створюється формами  , де
, де 
Форми  утворюють базис, спряжений з базисом-
утворюють базис, спряжений з базисом- 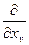 , v=1,…,n простору
, v=1,…,n простору  .
.
Виходячи з базиса {  } простору Е1, ми побудуємо деякі базиси спеціального вигляду в просторах Ер і підрахуємо розмірність цих просторів.
} простору Е1, ми побудуємо деякі базиси спеціального вигляду в просторах Ер і підрахуємо розмірність цих просторів.
Твердження 1. а) При р>n кожна диференціальна р-форма 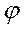 рівна нулю.
рівна нулю.
б) Якщо зовнішня р-форма  приймає нульові значення на всіх р-наборах виду
приймає нульові значення на всіх р-наборах виду
 , де
, де  то
то 
Твердження 2. Мають місце рівності

0, якщо  ,
,
+1, якщо  отримується з
отримується з  за допомогою парного числа транспозицій,
за допомогою парного числа транспозицій,
-1, якщо це число транспозицій непарне.
Теорема 2.1. Для кожного р  0 розмірність
0 розмірність  ; р-форми спеціального виду
; р-форми спеціального виду
 , де
, де 
при р  1 створює базис простору
1 створює базис простору 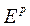 . Тому кожну форму
. Тому кожну форму  можна єдиним чином записати у вигляді
можна єдиним чином записати у вигляді
 .
.
Твердження 3. Має місце рівність  .
.
Теорема 2.2. Якщо  і
і 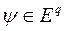 , то
, то 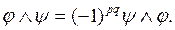
Цей так називаючий знакозмінний закон замінює звичайний комутативний закон.

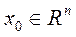 . Позначимо через
. Позначимо через 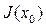 множину всіх функцій f,визначених в деякому (залежному від f) околі U точки
множину всіх функцій f,визначених в деякому (залежному від f) околі U точки  і неперервних в точці
і неперервних в точці  . А через
. А через  множину тих функцій
множину тих функцій  , які, крім того, диференційовані в точці
, які, крім того, диференційовані в точці  ,
,  випливає, що
випливає, що  . Дотичним вектором в точці
. Дотичним вектором в точці  , що володіє слідуючими додатковими властивостями:
, що володіє слідуючими додатковими властивостями:
 ,
,  , то
, то  ;
;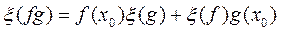 при
при  .
. утворюють n-вимірний векторний простір
утворюють n-вимірний векторний простір  , який утворюється частинними похідними
, який утворюється частинними похідними  , v= 1 ,…,n. При цьому
, v= 1 ,…,n. При цьому  - це дотичний вектор, що визначається умовою
- це дотичний вектор, що визначається умовою  . Простір
. Простір  є векторним простором пфаффовых форм в точці х0. Цей простір створюється формами
є векторним простором пфаффовых форм в точці х0. Цей простір створюється формами  , де
, де 
 утворюють базис, спряжений з базисом-
утворюють базис, спряжений з базисом- 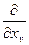 , v=1,…,n простору
, v=1,…,n простору 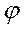 рівна нулю.
рівна нулю. приймає нульові значення на всіх р-наборах виду
приймає нульові значення на всіх р-наборах виду , де
, де  то
то 

 ,
, отримується з
отримується з  за допомогою парного числа транспозицій,
за допомогою парного числа транспозицій, 0 розмірність
0 розмірність  ; р-форми спеціального виду
; р-форми спеціального виду , де
, де 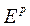 . Тому кожну форму
. Тому кожну форму  можна єдиним чином записати у вигляді
можна єдиним чином записати у вигляді .
. .
. і
і 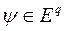 , то
, то