Грасманові добутки векторного простору
Літерою Т ми будемо позначати деякий дійсний векторний простір, а символом Т* — простір, спряжений з Т, тобто векторний простір лінійних форм в просторі Т. Символом Тр ми будемо позначати р-кратний декартовий добуток простору Т на себе, тобто множину всіх р-наборів Означення 1.1. Р-лінійною формою (де р
що має сідуючі властивості: 1) для кожного
2) при
0-лінійною формою називається дійсне число. Таким чином, р-лінійна форма Іноді вимагаються більш загальні поняття: Означення 1.2. (р, q)-лінійною формою в просторі Т (де р і q
лінійне відносно кожної окремої змінної; р-форми в просторі Т називають також (р, 0)-лінійними формами, а q-форми в просторі Т* називаються (0, q)-лінійними формами в просторі Т. Таким чином, при а,
Векторний простір, створений (р,q)-формами, ми будемо позначати символом В подальшому нам будуть майже всюди зустрічатися р-форми. Означення 1.3. р-лінійна форма
Кожна 1-лінійна форма (при р=1) є зовнішньою. Зовнішніми 0-формами ми за означенням вважаємо дійсні числа. Замість «зовнішня» часто говорять «альтернована» або «кососиметрична»; всі ці терміни означають одне і теж. Теорема 1.1. Для кожного р зовнішні р-форми створюють дійсний векторний простір Ер, що називається р-кратним грасмановим добутком над простором Т. При цьому Насправді, разом з формами З означення випливає, що: 1) Якщо
2) Якщо
Щоб встановити подальші властивості зовнішніх р-форм, ми введемо символ Кронекера. Означення 1.4. Для будь-яких двох натуральних чисел
Якщо
Функція Таким чином, символ Кронекера Властивість 1. З цієї властивості випливає проста інтерпритація символа Кронекера. Тобто, якщо серед чисел
і, значить, оскільки Р-набором ( Символ Кронекера слугує для того, щоб «альтернувати» довільну р-лінійну форму. Як відомо, множину з р об’єктів можна упорядковувати рівно р! різними способами. Таким чином, кожному р-набору векторів Означення 1.5. Нехай
Якщо р=0, то ми покладаємо [ Наприклад, при р=2
У випадку р=1, природньо [ Тведрження 2. Якщо Твердження 3. Форма [ Твердження 4. [[ Має місце тривіальне твердження. Твердження 5. Якщо Тепер ми визначимо добуток полілінійих форм. Нехай
де
яке ми будемо називати добутком форм 1) 2) 3) 4) Твердження 6. Означення 1.6 Нехай
Таким чином, Теорема 1.2. а) б) в) г) Як видно вже з тривіальних прикладів, зовнішній добуток не комутативний. Що виникає при перестановці співмножників, найлегше всього вияснити, скориставшись базисом простору Т.
|

 , елементів простору Т.
, елементів простору Т. 1) в просторі Т називається відображення
1) в просторі Т називається відображення ,
, , що задовольняє умову
, що задовольняє умову  ,
,
 і
і 

 є функція від р векторів, лінійна відносно кожної окремої змінної; 1-лінійні форми просто являються елементами спряженого простору Т*. Точно так, як і у випадку 1-лінійних форм, можна показати, що р-лінійні форми створюють дійсний векторний простір. Число р називається порядком форми
є функція від р векторів, лінійна відносно кожної окремої змінної; 1-лінійні форми просто являються елементами спряженого простору Т*. Точно так, як і у випадку 1-лінійних форм, можна показати, що р-лінійні форми створюють дійсний векторний простір. Число р називається порядком форми 

 і
і  маємо
маємо
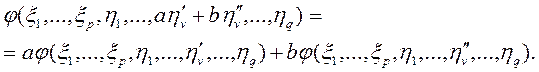
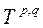 .
. називається зовнішньою р-формою, якщо для кожного
називається зовнішньою р-формою, якщо для кожного 

 і
і 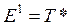 .
. і
і  і форма
і форма  є зовнішньою; якщо
є зовнішньою; якщо  і
і  , то
, то  .
. , то
, то
 при
при  , то
, то
 i
i  покладемо:
покладемо: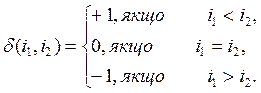
 і
і  — який-небудь р-набір натуральних чисел, то покладемо
— який-небудь р-набір натуральних чисел, то покладемо
 називається символом Кронекера. Крім того, для кожного натурального числа і покладемо
називається символом Кронекера. Крім того, для кожного натурального числа і покладемо 
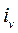 і
і  при
при 
 , які ми вважаємо попарно різними, будемо створювати транспозиції до тих пір, поки числа
, які ми вважаємо попарно різними, будемо створювати транспозиції до тих пір, поки числа  , то при кожній окремій транспозиції знак символа
, то при кожній окремій транспозиції знак символа  зміниться. Якщо а — число всіх проведених транспозицій, то
зміниться. Якщо а — число всіх проведених транспозицій, то
 1,
1,  .
. ) визначається не саме число а, але, як показує це припущення, число
) визначається не саме число а, але, як показує це припущення, число  , тобто «парність» числа а.
, тобто «парність» числа а. можна, міняючи місцями вектори
можна, міняючи місцями вектори  , поставити в відповідність р! елементів
, поставити в відповідність р! елементів  . Розуміється, всі ці елементи відрізняються один від одного лише в тому випадку, якщо
. Розуміється, всі ці елементи відрізняються один від одного лише в тому випадку, якщо  при
при  .
.
 де
де  і
і 
 — дві р-лінійні форми, то
— дві р-лінійні форми, то 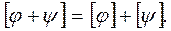 Для кожного
Для кожного  має місце рівність
має місце рівність  .
.
 і
і  — вектори з Т. Ця формула визначає (р+q)-лінійне відображення
— вектори з Т. Ця формула визначає (р+q)-лінійне відображення
 і
і  . Відразу перевіряємо слідуючі правила:
. Відразу перевіряємо слідуючі правила:


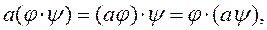 де
де  .
. .
. — зовнішня р-форма и
— зовнішня р-форма и  — зовнішня q-форма. Зовнішнім добутком форм
— зовнішня q-форма. Зовнішнім добутком форм  і
і  .
.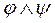 є зовнішньою (р+q)-формою. Зовнішній добуток не є добутком в Ер, бо при р>0 добуток двох р-форм не лежить в Ер. Зовнішній добуток відображає декартовий добуток
є зовнішньою (р+q)-формою. Зовнішній добуток не є добутком в Ер, бо при р>0 добуток двох р-форм не лежить в Ер. Зовнішній добуток відображає декартовий добуток  в просторі
в просторі 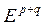 .
. де
де  ,
,  ;
;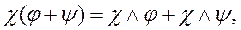 де
де  ,
, 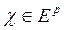 ;
; де
де  ,
, 
 ;
; де
де 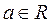 ,
, 


