Векторний і координатний запис формули Стокса
Нехай замкнена кусково-гладка крива Г являється межею кусково-гладкої поверхні S. Нехай поверхня S міститься в деякій трьохмірній області G
при чому напрямок контуру Г (в криволінійному інтегралі) і вибір додатного напрямку нормалі (в поверхневому інтегралі) узгоджені за «правилом буравчика» - додатною рахується та сторона поверхні, на якій додатній напрямок контуру відповідає руху проти часової стрілки (див мал.1).
Рис.1. Узгодження орієнтації в формулі Стокса Не важко побачити, що у випадку, коли крива Г лежить в площині xOy, формула Стокса переходить в відому формулу Гріна, яка зв’язує криволінійний інтеграл першого роду по плоскій кривій з подвійним інтегралом по області, обмеженій даною кривою (див. рис.2).
Рис.2. Обхід границі області в формулі Гріна Загальний випадок формули Стокса формально виходить з формули Гріна циклічною перестановкою координат: x→y→z→x, P→Q→R→P Нехай
де
Рис.3. Направляючі косинуси нормалі
Оскільки зв'язок між поверхневими інтегралами першого і другого роду задається формулою
Формулу Стокса можна переписати у вигляді (рис.3.):
При знаходженні визначника третього порядку під «множенням» знака диференціювання (наприклад, Розглянемо вектор
Не важко побачити, що під знаком поверхневого інтеграла першого роду стоїть скалярний добуток вектора
який називається ротором вектора
то ротор можна формально представити, як векторний добуток вектора «набла» на вектор F:
Позначимо радіус-вектор довільної точки простору
Введемо вектор елементарного переміщення
тоді формулу Стокса можна записати у векторній формі:
Криволінійний інтеграл по замкнутому контуру називається циркуляцією векторного поля, поверхневий інтеграл другого роду означає потік через поверхню. Отже, формула Стокса, допускає наступне словесне формулювання: циркуляція векторного поля по замкнутому контуру дорівнює потоку його ротора через поверхню, що стягується цим контуром.
|

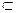 R3, у всіх точках якої визначені і неперервні функції трьох змінних P, Q, R, а також їх частинні похідні. Тоді криволінійний інтеграл другого роду по кривій Г пов’язаний з поверхневим інтегралом другого роду по поверхні S формулою Стокса:
R3, у всіх точках якої визначені і неперервні функції трьох змінних P, Q, R, а також їх частинні похідні. Тоді криволінійний інтеграл другого роду по кривій Г пов’язаний з поверхневим інтегралом другого роду по поверхні S формулою Стокса: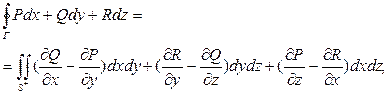

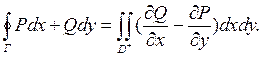
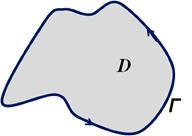
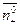 - одиничний вектор зовнішньої нормалі до поверхні S. Тоді
- одиничний вектор зовнішньої нормалі до поверхні S. Тоді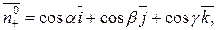
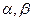 і
і 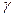 - кути, які утворює цей вектор з координатними осями (косинуси цих кутів називають «направляючими косинусами»).
- кути, які утворює цей вектор з координатними осями (косинуси цих кутів називають «направляючими косинусами»).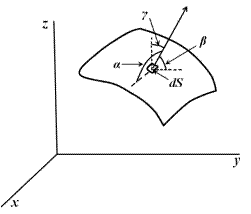
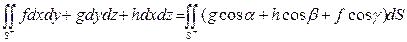 ,
,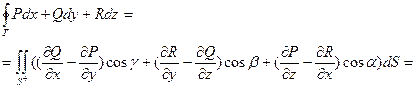
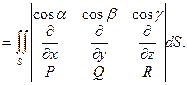
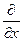 ) на функцію підрозумовується знаходження відповідної частинної похідної.
) на функцію підрозумовується знаходження відповідної частинної похідної.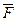 , координатами якого є величини P, Q, і R:
, координатами якого є величини P, Q, і R: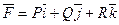 .
.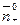 на вектор
на вектор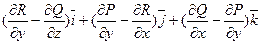 ,
,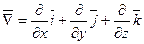 ,
,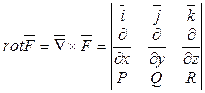 .
. . Відомо, що координати радіус-вектора є координатами точки, на яку він вказує:
. Відомо, що координати радіус-вектора є координатами точки, на яку він вказує: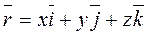 .
.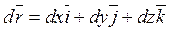 ,
,



