Загальне означення алгебриОсновная литература 1. Ионин А.А. и др. Теплоснабжение - М.: Стройиздат, 1982. -336 с. 2. Соколов Е.А. Теплофикация и тепловые сети. 5-изд. - М.: Энергоиздат, 1982. -360 с. Дополнительная литература: 3. Апарцев М.М. Наладка водяных систем централизованного теплоснабжения. Справочное пособие. - М.: Энергоатомиздат, 1983. -204 с. 4. Манюк В.И. и др. Справочник по наладке и эксплуатации водяных тепловых сетей. - 3-изд. - М.: Стройиздат, 1988. -232 с. 5. Козин В.Е. и др. Теплоснабжение Уч. пособие. - М.: Высшая школа, 1980. -408 с. 6. Водяные тепловые сети. Справочное пособие по проектированию. Под. ред. Н.К.Громова, Е.П.Шубина. М.: Энергоатомиздат,1986.- 376с.
ЗМІСТ ВСТУП …………………………………………………………………… РОЗДІЛ 1. ТЕОРЕТИЧНА ЧАСТИНА………………………………… 1.1 Загальне означення алгебри………………………………………… 1.2 Грасманові добутки векторного простору………………………….. 1.3 Зовнішні диференціальні форми……………………………………. 1.4 Диференційовані відображення……………………………………… 1.5 Диференціальні форми на допустимих множинах………………… 1.6 Приклади і правила дій……………………………………………… РОЗДІЛ 2. ПРАКТИЧНА ЧАСТИНА…………………………………. 2.1 Формула Стокса……………………………………………………… ВИСНОВОК ……………………………………………………………… СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ ……………………….. ВСТУП Актуальність обраної проблеми. В багатьох математичних і фізичних додатках теорії інтегрування недостатньо інтегрувати функції по всьому простору або по його вимірним підмножинам; необхідно знаходити інтеграли вздовж шляхів (криволінійні інтеграли) і по частинам поверхонь. Так, наприклад, щоб обрахувати роботу при русі точки в силовому полі, необхідно «просумувати силу вздовж лінії», тобто розглянути деякий криволінійний інтеграл вздовж пройденого цією точкою шляху. Подібним чином, кількість електроенергії, що протікає через криву поверхню, виражається поверхневим інтегралом і т. д. Спроба звести ці фізичні і аналогічні математичні питання в систему понять, якими можна було б легко оперувати, приводить до визначення поняття зовнішньої (або альтернованої) диференціальної форми. Об’єкти, які ми інтегруємо по р-вимірній частині поверхні в Rn, є диференціальними формами порядку р, а не функціями. Векторний аналіз з його бачаточисленними диференціальними операторами (grad f, rot a, div a) і інтегральними формулами є навряд чи доцільним, але часто дуже заплутаним перекладом обчислення зовнішніх диференціальних форм. Отже, мета роботи: введення та опис поняття диференціальної форми, основних операцій над ними; показ доцільності використання диференціальних форм в задачах, що зводяться до обчислення інтегралів від функції багатьох змінних та обчислення параметрів векторних полів, ілюстрація переваги використання алгебри диференціальних форм перед методами векторного аналізу.
Завдання: 1) Описати основні об’єкти векторного аналізу 2) Описати алгебру диференціальних форм 3) Встановити зв’язок між ними РОЗДІЛ 1. ТЕОРЕТИЧНА ЧАСТИНА Загальне означення алгебри Алгебра (від арабського «аль-джебр», частина назви трактату «Китаб аль-джебр валь-мукабала» («Повна книга обчислень шляхом доповнення і рівноваги») узбецького математика і астронома Аль-Хорезмі) – 1) розділ математики, що вивчає властивості дій над різноманітними величинами і розв’язки рівнянь, пов’язаних з цими діями; 2) розділ математики, що вивчає системи об’єктів довільної природи, в яких визначено алгебраїчні операції, аналогічні своїми властивостями діям над числами. Види алгебр: асоціативна, лінійна, алгебра многочленів, функцій, векторний добуток, як векторна алгебра і т. д.. Кільце́;—це алгебраїчна структура, в якій визначені операції додавання та множення з властивостями подібними до додавання і множення цілих чисел. Кільце R — це множина з двома бінарними операціями, що звичайно позначаються "+" та " · (R,+) є комутативною групою. Її називають адитивною групою кільця і нейтральний елемент в ній позначають як 0 (нуль); · · · в Деякі автори не вимагають наявності одиниці, і натомість називають кільця з одиницею унітарними кільцями або кільцями з одиницею. Розглядаються також кільця, у яких не задовільняється асоціативність множення, наприклад, кільця (або алгебри) Лі. У такому разі, кільця, в яких множення асоціативне, називають асоціативними кільцями. Кільця, що задовольняють вимогу комутативності множення Символ Якщо для двох елементів кільця a та b виконується рівність ab=ba=1 то кажуть, що b є оберненим елементом до Якщо в кільці немає дільників нуля, відмінних від самого нуля, тобто якщо з ab=0 витікає, що або a=0, або b=0, то кажуть про кільце без дільників нуля. Якщо до того ж кільце є комутативним, то його називають цілісним.
|
" і називаються додаванням та множенням, яка задовільняє наступній системі аксіом:
(дистрибутивність додавання щодо множення);
(асоціативність множення);
існує нейтральний елемент 1 (одиниця), що задовільняє: 
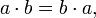називають комутативними кільцями. Не всі кільця є комутативними, наприклад, кільце матриць чи кватерніонів.
зазвичай не пишуть, використовуючи стандартні правила порядку операцій, тому, наприклад, a=bc є скороченим записом 
.
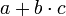відносно множення. В цьому випадку елемент b однозначно визначається елементом a і позначається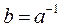 
(звичайно, маємо також, що 
).
