Інваріантне («фізичне») означення ротора
Ротор є одним з диференціальних операторів першого порядку. Формальне визначення ротора справляє враження деякої штучності цього оператору, залишається незрозумілим, чим принципово відрізняється ротор від інших можливих комбінацій частинних похідних першого порядку. Серед усіх можливих операторів мати фізичний зміст, а значить і представляти інтерес, можуть тільки ті, які описують об'єктивні властивості, тобто ті властивості векторного поля, які не залежать від спостерігача, і, отже, не змінюються при переході до будь-якої іншої системи координат. При формальному визначенні ротора той факт, що він виявляється однаковим у будь-якій системі координат, є зовсім неочевидним. Формула Стокса дозволяє показати інваріантність ротора щодо вибору системи координат і виявити його фізичний зміст. Нехай задана деяка точка простору М0. Розглянемо деяку площину
Рис.4. Фізичне значення ротора За формулою Стокса маємо
Застосовуючи теорему про середнє, отримуємо
де М - деяка (взагалі кажучи, невідома) точка області D, а SD позначає площу області D. Звідси отримуємо, що
Тепер почнемо «стягувати» контур Г в точку М0, тобто будемо розглядати області все меншої площі, але обов'язково всі, що містять точку М0. При граничному переході
Отримаємо:
Ясно, що при необмеженому зменшенні розмірів області D довжина контуру, а отже і циркуляція, прямують до нуля, тому під знаком границі ми маємо невизначеність виду За визначенням скалярного добутку
Де
Таким чином, абсолютна величина ротора відповідає максимальній (по всіх можливих напрямках) інтенсивності обертальної компоненти векторного поля, а напрямок ротора відповідає нормалі до площини, в якій обертальна компонента найбільша. Останнє співвідношення можна взяти в якості визначення ротора. При такому визначенні незалежність ротора від вибору системи координат очевидна.
|

 , що проходить через точку М0. Нехай
, що проходить через точку М0. Нехай  - одинична нормаль до цієї площини. Нехай D деяка область у площині
- одинична нормаль до цієї площини. Нехай D деяка область у площині 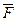 , напрямок обходу і орієнтацію нормалі вважаємо узгодженими (див. рис.4.).
, напрямок обходу і орієнтацію нормалі вважаємо узгодженими (див. рис.4.).
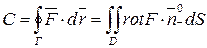 .
. ,
,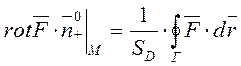 .
.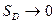 діаметр області також буде прямувати до нуля, а значить
діаметр області також буде прямувати до нуля, а значить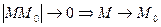
 .
.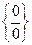 . Сама границя означає інтенсивність обертальної компоненти векторного поля.
. Сама границя означає інтенсивність обертальної компоненти векторного поля. ,
,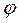 - кут між нормаллю і вектором. Найбільшого значення скалярний добуток досягає, коли напрямок нормалі і ротора співпадають. В цьому випадку
- кут між нормаллю і вектором. Найбільшого значення скалярний добуток досягає, коли напрямок нормалі і ротора співпадають. В цьому випадку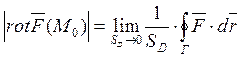 .
.


