Задача 3. Обчислити циркуляцію вектора по контуру трикутника NPM: M(2;0;0), N(0;3;0), P(0;0;1).
Обчислити циркуляцію вектора Розв’язання: Точки M, N I P лежать на координатних осях, відсікаючи на них відрізки, відповідно, 2, 3 і 1 (див. рис.10.).
Рис.10. Схема до задачі 5. Для запису рівняння площини MNP зручно використовувати рівняння площини у відрізках:
Домноживши обидві частини рівняння на 6, отримаємо: 3х+2у+6z-6=0. Знайдемо ротор
Додатна нормаль створює гострі кути зі всіма координатними осями, зведемо поверхневий інтеграл другого роду до трьох подвійних:
Враховуючи властивості подвійного інтегралу, а саме, що інтеграл від одиниці дорівнює площі поверхні інтегрування, маємо, що подвійні інтеграли дорівнюють площам відповідних трикутників ВИСНОВОК
СПИСОК ЛІТЕРАТУРИ: 1. Зорич В.А. Математический анализ часть II.- М.: ФАЗИС; Наука; Ч.II. - 1984, 640с. 2. Кудрявцев Л.Д. Курс математического анализа том 2. - М.: Дрофа, 2004. - 720 с. 3. Будак Б.М. Фомин С.В. Кратные интегралы и ряды. - М.: Наука, 1965. 4. Гюнтер Н.М. Теория потенциала и ее применение к основным задачам математической физики. - М.: ГИТТЛ, 1953. 5. Дороговцев А.Я. Элементы общей теории меры и интеграла.- К.: Высшая шк. Головное изд-во, 1989.- 152с., 2 ил.- Библиогр.: 16 назв. 6. Грауэрт Г., Либ И., Фишер В. Дифференциальное и интегральное исчисления. – М.: Изд-во «Мир», 1971. 7. Гелбаум Б., Олмстед Дж. Контрпримеры в анализе, М., «Мир», 1967. 8. Курант Р. Курс дифференциального и интегрального исчисления (2 тома), М., 1967. 9. Смирнов В. И. Курс высшей математики (5 томов). 10. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления (3 тома), М., 1960. 11. Картан А. Дифференциальное исчисление. Дифференциальные формы.-М.: Мир, 1971. 12. Рудин У. Основы математического анализа. – М.: Мир, 1976. 13. Шилов Г.Е. Математический анализ, специальный курс, 2-е изд. – М.:1961. 14. Спивак М. Математический анализ на многообразиях. – М.: Мир, 1968. 15. Шварц Л. Анализ. Том 2. - М: Мир, 1972. 16. Постников М. М. Лекции по геометрии. Семестр III. Гладкие многообразия. — М.: Наука, 1987. 17. Кострикин А.И. Введение в алгебру. Часть 1. Основы алгебры. – М.: 2004 18. Винберг Э.Б. Курс алгебры. 2-е изд., испр. и доп. – М.: Изд-во «Факториал Пресс», 2001. – 544 с. 19. Булдырев В. С., Павлов Б. С. Линейная алгебра и функции многих переменных. — Л.: Издательство Ленинградского университете, 1985. 20. В. И. Арнольд. Математические методы классической механики. — 3-е изд. — М.: Наука, 1989. — 472 с 21. Болибрух А. А. Уравнения Максвелла и дифференциальные формы. – М.: МЦНМО, 2002. 22. Аграчев А.А., Сачков Ю.Л. Геометрическая теория управления. - М.: ФИЗМАТЛИТ, 2005. 23. Петрова Л. И. Кососимметричные дифференциальные формы. Законы сохранения. Основы теории поля. М.: Ленанд, 2006. 24. Ботт Р, Ту Л.В. Дифференциальные формы в алгебраичской топологии. М.: Наука, Гл. ред. физ.-мат. лит., 1989. 336 с
|

 по контуру трикутника NPM: M(2;0;0), N(0;3;0), P(0;0;1).
по контуру трикутника NPM: M(2;0;0), N(0;3;0), P(0;0;1).




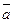 і застосуємо формулу Стокса:
і застосуємо формулу Стокса:


 .
.


