Выпуклость функции
Опр.: График функции
Теорема (достаточное условие выпуклости). Если вторая производная дважды дифференцируемой функции положительна (отрицательна) внутри некоторого промежутка Х, то функция выпукла вниз (вверх) на этом промежутке.
Опр.: Точка В точке перегиба касательная пересекает график функции, т.к. он переходит (перегибается) с одной стороны касательной на другую.
Теорема (необходимое условие существования точки перегиба). Если в точке
Опр.: Точки графика функции
Теорема (достаточное условие существования точки перегиба). Если в некоторой окрестности точки
Схема исследования функции 1). Найдите вторую производную 2). Найдите критические точки 2-го рода функции, в которых вторая производная равна нулю или не существует. 3). Исследуйте знак второй производной слева и справа от каждой критической точки и сделайте вывод об интервалах выпуклости и наличии точек перегиба. 4). Найдите значения функции в точках перегиба.
Пример: Найти промежутки выпуклости и точки перегиба функции f (x) = x 3 – 3 x 2 + 1. Решение: 1). Найдём вторую производную
2). Найдём критические точки 2-го рода: 3). Исследуем знак второй производной.
4). Найдём значение функции в точке перегиба: f (1) = -1; (1; -1) – координаты точки перегиба (рис.1).
Рис. 1. График функции f (x) = x 3 – 3 x 2 + 1.
|

 имеет на интервале
имеет на интервале  выпуклость вверх (вниз), если на этом интервале график расположен не выше (не ниже) касательной к графику функции, проведённой в любой точке этого интервала.
выпуклость вверх (вниз), если на этом интервале график расположен не выше (не ниже) касательной к графику функции, проведённой в любой точке этого интервала. называется точкой перегиба графика функции
называется точкой перегиба графика функции  , в пределах которой график функции
, в пределах которой график функции  в точке
в точке  = 0.
= 0. .
.

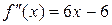 .
.

 < 0 при
< 0 при 
 кривая выпукла вверх;
кривая выпукла вверх;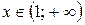
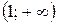 кривая выпукла вниз (вогнута). Точка х = 1 является точкой перегиба.
кривая выпукла вниз (вогнута). Точка х = 1 является точкой перегиба.



