Анализ реакции рынка на изменение ситуации
Ранее уже говорилось о влиянии на рыночные процессы и явления целого комплекса факторов, как социально-экономических и демографических, так и естественно-природных,. Рынок чутко реагирует на внешние воздействия. Благоприятное влияние заставляет рынок оживляться и расширяться, действие негативных сил приводит к сокращению деловой активности, сжатию рынка, вплоть до коллапса. Особенно подвержены влияниям такие рыночные категории, как спрос и предложение, т.е. основные элементы рыночного механизма. В качестве их раздражителей на первый план выдвигаются цены и денежный доход потребителей, причем если предложение детерминировано волей и интересами производителей/поставщиков, то спрос складывается как результат множества составляющих, имеющих вероятностный, стохастический характер. Конечно, изменения и колебания предложения находят отражение в коммерческих документах, контрактах, а изменения и колебания спроса проявляются непосредственно на рынке в форме тенденций в результате действия закона больших чисел. Спрос и предложение изменчивы и реактивны. Это явление принято называть эластичностью.
Таким образом, эластичность спроса и предложения - явление специфически рыночное, обусловленное проявлением действия рыночных законов, эластичность которых проявляется в чрезвычайной гибкости и изменчивости, зависимости от влияния различных социально-экономических факторов, в первую очередь таких, как цена и денежный доход. Некоторые исследователи[49] делят эластичность на: • кратковременную, когда покупатели временно сокращают покупки, реагируя тем самым на шок, вызванный скачком цен (в этом случае спрос довольно быстро восстанавливается под влиянием компенсирующих факторов); • долговременную, когда изменение спроса происходит длительный период. Следует отметить, что векторы действия факторов на спрос и предложение противоположны, полярны. Рост цен, например, приводит к сокращению спроса, но к увеличению предложения, что является проявлением действия закона стоимости. Спрос на потребительском рынке реагирует на изменения цен и дохода практически мгновенно, а на оптовом - с определенным лагом, поскольку он в какой-то мере детерминирован направленной деятельностью оптовых коммерсантов, основанной на той или иной маркетинговой стратегии, использующей различные методы стимулирования спроса. То же можно сказать и о предложении, эластичность которого проявляется в организованных формах контрактных (договорных) связей поставщиков и оптовых покупателей. Здесь существенным элементом эластичности является время, в течение которого оптовый продавец приспосабливается к изменению цен.. Конечно, время реакции на изменения цен зависит от целого ряда условий, в частности от развитости систем информации. На феномен чувствительности (иногда говорят: чуткости) спроса и предложения от воздействия внешних факторов исследователи социально-экономических процессов обратили внимание еще в начале XIX в. Французский экономист О. Курно высказал мнение, что в определенном смысле спрос есть функция цены. Эту идею впоследствии развил английский исследователь А. Маршалл, выразивший ее в виде формулы
где В - спрос (англ, demand); р - цена (англ. рriсе).
Многие исследователи, занимаясь оценкой влияния цен на спрос, заметили, что спрос на каждый товар зависит не только от цены этого товара, но и от цен на другие товары. В 80-х годах прошлого века швейцарский экономист Л. Вальра, представитель так называемой лозаннской школы, на основе первичного уравнения, предложенного О. Курно, представил свой вариант эластичности спроса в виде формулы
где dx - спрос товара X; рx - цена товара X; р1, p2,…, pn - цены других товаров.
На этой идее базируется теория перекрестной эластичности, получившая развитие впоследствии. Мы в дальнейшем вернемся к ней. Взгляды Курно - Маршалла в последующие годы были развиты другими видными исследователями (в частности, В. Парето, Е. Слуцким, Д. Хиксом и др.), которые ввели в понятие эластичности фактор дохода. Об эластичности спроса от факторов цены и дохода писал также К. Маркс в «Капитале»[50]. Известный создатель теории «экономике» П. Самуэльсон рассматривает эластичность спроса от цен как степень реакции покупаемого количества товара от колебаний рыночных цен[51]. Следует обратить внимание, что у цены и дохода обратные векторы влияния на спрос: при увеличении цены спрос, как правило, падает, а при увеличении дохода спрос, опять-таки как правило, растет (хотя из этого правила есть исключения). Меру эластичности определяет количественный показатель - коэффициент эластичности, предложенный А. Маршаллом в виде следующего отношения:
где Э - коэффициент эластичности, выраженный в процентах; Dy - прирост результативного признака, в частности спроса или предложения; Dx - прирост факторного признака, в частности цены или дохода; у - базовое значение результативного признака (спроса); x - базовое значение факторного признака (цены, дохода).
Довольно часто эту формулу используют в преобразованном виде:
Результат, т.е. значение коэффициента эластичности, может быть равен 1, а также больше или меньше ее. Если Э < 1 обнаруживается явление инфраэластичности, товар мало эластичен или полностью неэластичен, т.е. практически не реагирует на изменение факторного признака. При Э > 1 отмечается явление ультраэластичности, товар является эластичным или сильно эластичным, т.е. он заметно реагирует на внешние воздействия. При Э = 1 товар является слабоэластичным (обнаруживается так называемый унитарный спрос), в этом случае, как правило, спрос нейтрально относится к попыткам влиять на него, он изменяется пропорционально изменениям факторного признака. Следует учитывать знаки коэффициента эластичности. Его положительное значение свидетельствует, что при увеличении факторного признака спрос растет, т.е. связь прямая (обычно такая зависимость проявляется от дохода); отрицательное значение - что при увеличении факторного признака спрос сокращается, т.е. связь обратная; такая зависимость спроса характерна при воздействии цен (рис. 5.7). Расчет коэффициента эластичности спроса - необходимый этап как в стратегическом, так и в конъюнктурном анализе, обеспечивающий информационно-аналитические потребности формирования системы регулирования спроса (иногда ее называют системой ФОССТИС[52]), регулирование этапов жизненного цикла товаров, плановых расчетов и т.д.
Пример 1. За месяц до изменения цен в среднем за день продавалось 50 кг товара А, по новым ценам продавалось 30 кг товара. Цена выросла с 10 ло 15 т/б./кг:
рост цены на 1% приводит к сокращению спроса на 0,8%, т.е. имеет место инфраэластичность.
Пример 2. Средний доход определенной группы населения в расчете на одного члена семьи вырос с 400 до 600 руб., расходы на покупку увеличились с 250 до 375 руб.:
т.е. имеет место унитарный спрос.
Пример 3. Цена товара Б в нашем магазине - составляет 30 руб. за штуку. В магазине конкурента цена на аналогичный товар - 50 руб. За сопоставимый период наш магазин продал 320 штук товара Б, а конкуренту удалось реализовать всего 200 штук: Dу = 320 - 200 = + 120; Dх = 30 - 50 = -20; у = 200; х = 50. В третьем примере мы показали, что расчет коэффициента эластичности может вестись не только по динамическим показателям, но и по статичным, когда идет сравнение по двум предприятиям, регионам и т.д. Один из них принимается за базу сравнения, а понятие прироста (А) трактуется как «разность», «отклонение» и т.п.
Это означает, что спрос ультраэластичен и нашей фирме имеет смысл продолжать ценовую конкурентную борьбу.
Надо иметь в виду, что существуют товары, которые иначе реагируют на изменение цен и дохода. Во-первых, рост дохода приводит к падению спроса на товары невысокой потребительной ценности. Во-вторых, утверждение, что вектор влияния цен на спрос находится в обратном отношении к вектору влияния дохода, не носит характера императива. Из этого правила имеется несколько исключений. Прежде всего на эластичность влияет степень полезности товара (т.е. его ранг в иерархии потребностей). Чем важнее товар для потребления, тем он обычно менее эластичен. Существует явление, называемое парадоксом Джиффена: чем дороже хлеб, тем больше его покупают. Инфляция снижает спрос в первую очередь на высококачественные, дорогостоящие товары, не фигурирующие в шкале потребностей на первых местах. В условиях роста цен их покупают меньше, чем диктуют требования эластичности, а взамен покупают товары первой необходимости. Это означает, что один товар в спросе замещается другим. Эффект замещаемости проявляется в том, что снижение цены делает его более, а рост цены - менее конкурентоспособным. Это приводит к тому, что в первом случае он теснит другой товар (становится его субститутом), а во втором - сам вытесняется более дешевым товаром. Данный случай вписывается в известную в маркетинге матрицу конкуренции Портера, которая будет приведена в 5.6, где речь идет о конкуренции товаров. Из экономической истории известен также факт роста спроса на картофель при повышении спроса на него. В конце прошлого века во время голода в Ирландии росли цены на все продукты, но по сравнению с другими продуктами питания цены на картофель были доступнее беднякам. Тогда же родилось выражение: картофель - хлеб бедных. Явление это называют эффектом Гриф-фина, по имени английского ученого, который дал его описание. Одновременно проявляется действие другого парадокса - парадокса Вебелена. Он заключается в том, что предметы роскоши покупаются не столько ради их потребительских свойств, сколько ради их социального значения, в частности престижности, моды и т.п. Это вполне согласуется с теорией мотивации потребностей, разработанной известным американским экономистом и социологом и известной под названием пирамиды Маслоу. Потребность в самоутверждении и самовыражении находится на вершине этой пирамиды. Представьте себе богатого российского предпринимателя, который покупает роскошный мерседес. Он делает это не только потому, что этот автомобиль действительно удобен и надежен, но прежде всего потому, чтобы поддержать свой престиж. Положение обязывает, как говорят французы. Французский экономист Р. Бадуэн указывал, что эффект Джиффена порожден бедностью, а эффект Вебелена - богатством. Из приведенных выше примеров видно, что коэффициент эластичности отражает реакцию потребителей на изменение факторов как во времени (динамическая эластичность), так и в пространстве (сравнительная эластичность). В первом случае мы рассматриваем прирост результативного и факторного признаков как разность уровней текущего и базисного периодов:
Во втором случае прирост - это отклонение уровня одной территориальной или социальной единицы от другой. Например, различия в товарообороте и ценах двух конкурирующих фирм; при сравнении двух регионов; уровня покупок и дохода двух социальных групп населения (подобный пример будет рассмотрен в дальнейшем):
Это открывает некоторые возможности расширения границ анализа. Попробуем преобразовать формулу коэффициента эластичности спроса (динамического):
где Тпр. у - темп прироста результативного признака; Тпр. х - темп прироста факторного признака.
Пример. В базисном периоде было продано 20 т продукта по цене 25 руб. за 1 кг, в отчетном периоде - 14 т по цене 30 руб./кг. Это означает, что темп роста продажи продукта составляет 0,7 (темп прироста равен 0,7 - 1 = -0,3), а темп роста цены -1,2 (темп прироста равен 1,2 - 1 = 0,2). Традиционный расчет коэффициента эластичности:
т.е. при увеличении цены на 1% спрос на продукт снизился на 1,5% (спрос ультраэластичен). Упрощенный расчет коэффициента эластичности: Э = -0,3: 0,2 = -1,5, таким образом, получен тот же результат.
Традиционный коэффициент эластичности позволяет оценивать зависимость спроса от маркетинговых воздействий в динамике только для одного товара. Однако после замены исходных показателей отношением темпов прироста мы вправе осуществить одну подстановку: заменить однотоварные темпы прироста многотоварными общими индексами минус 1. В результате, с некоторой степенью условности, мы сможем выявить глобальное влияние цен на общую динамику спроса. Исчисленный в статике по ряду единиц (например, регионов) коэффициент эластичности может в зависимости от условий значительно варьировать по территории. Имеется возможность рассчитать средний коэффициент эластичности по всей совокупности единиц:
где Э - средняя эластичность по всей совокупности i-х единиц; Эi - эластичность спроса, определенная в i-м регионе (или социальной группе населения); М- вес i-й группы (товарооборот, численность населения, число семей и т.п.); n - число i-х единиц (регионов, групп и т.п.).
Расчет частных (групповых, региональных) коэффициентов эластичности имеет очень большое значение. Спрос различных социально-экономических групп потребителей по-разному реагирует на одни и те же факторы. Так, для потребителей с низким 1 уровнем дохода рост цен на 1% вызовет значительное снижение спроса, в то время как спрос потребителей с высоким уровнем дохода может не среагировать на этот ценовой «раздражитель». Или другой пример. По мере перехода из одной доходной группы в более высокую спрос на некоторые товары может возрастать не пропорционально, а с определенным ускорением или, наоборот, с замедлением - в зависимости от иерархии потребности, которую удовлетворяет данный товар. Эти закономерности эластичности спроса должны быть использованы в маркетинге в процессе сегментации рынка и в регулировании спроса. Известный немецкий экономист и социолог 80-х годов прошлого столетия Э. Энгель сформулировал закон, названный его именем: с увеличением дохода семьи ее расходы на питание растут абсолютно, но уменьшаются относительно. Аналогичный закон, связанный с эластичностью расходов на жилье, сформулировал немецкий статистик второй половины XIX в. А. Швабе: с ростом доходов семьи ее расходы на жилье растут абсолютно, но уменьшаются относительно. Следует также обратить внимание на то обстоятельство, что эластичность спроса проявляется не только в изменении его объема, но и в пропорциях и сдвигах его структуры. Рассмотрим методику расчета частных и среднего коэффициентов эластичности на условном примере группировки домохо-зяйств по душевому доходу. Для каждой социальной группы населения будет рассчитан коэффициент эластичности от дохода, а затем - средний коэффициент по всей совокупности домохозяйств. Исходные данные приведены в табл. 5.9. Показатели, необходимые для расчета среднего коэффициента эластичности, приведены в табл. 5.10. По итогам гр. 8 и 9 табл. 5.10 рассчитаны средние коэффициенты эластичности спроса от дохода. В качестве весов использованы частости распределения домохозяйств по уровню дохода без 1-й группы (гр. 1):
Таблица 5.9 Группировка домохозяйств по доходу (на одного человека за месяц)
Данные свидетельствуют о том, что влияние дохода в среднем в процессе перехода от малообеспеченных групп к высокообеспеченным в меньшей степени сказывается на спросе на продукты питания, чем на непродовольственные товары. Это согласуется с теорией мотивации потребностей, так как основная часть продуктов питания относится к группе предметов первой жизненной необходимости. Показательно, что 1% роста доходов в группах недостаточно обеспеченного населения вызывает более сильную реакцию потребителей, чем тот же процент в группах высокообеспеченного населения. Рассмотрим методику расчета. В табл. 5.9 приводятся исходные данные, табл. 5.10 является рабочей. В ней расчет начинается со 2-й строки, так как первая группа домохозяйств выступает для нее в качестве базы сравнения. Графа 1 представляет собой результат разности каждой последующей и предыдущей строк в табл. 5.9 (гр. 3). Графа 2 и графа 3 - результат деления в каждой предыдущей строке соответственно гр. 3 и гр. 4 в табл. 5.10 на гр. 2. Гр. 4 и гр. 5 представляют собой разность предыдущей и последующих строк соответственно гр. 3 и гр. 4 табл. 5.10. Графа 6 - результат последовательного деления отношения гр. 4 к гр. 1 на гр. 2, а гр. 7 - соответственно результат деления отношения гр. 5 к гр. 1 на гр. 3. В гр. 6 и гр. 7 представлены групповые коэффициенты эластичности спроса от дохода. В гр. 8 и гр. 9 производится взвешивание групповых коэффициентов эластичности по частостям распределения домохозяйств, гр. 6 и гр. 7 табл. 5.10 последовательно умножаются на гр. 1 табл. 5.9. В качестве примера приведем ход расчета по 2-й строке табл. 5.10.
Прирост факторного признака: Dх = 400 - 200 = 200 (гр. 1); • отношение результативного признака к факторному: по продуктам питания 122: 200 = 0,61 (гр.2); по непродовольственным товарам 30: 200 = 0,15 (гр. 3); • прирост результативного признака: по продуктам питания 400 - 200 =200 (гр. 4); по непродовольственным товарам 96 - 32 = 64 (гр. 5); • групповой коэффициент эластичности: по продуктам питания (200: 200): 0,61 = 1,64 (гр. 6); по непродовольственным товарам (66: 200): 0,15 = 2,2 (гр. 7); • взвешивание группового коэффициента эластичности: по продуктам питания 1,6 • 18 = 29,52 (гр. 8); по непродовольственным товарам 2,2 • 18 = 39,60 (гр. 9). В формуле эмпирического коэффициента эластичности заложено одно существенное противоречие: данный показатель отражает воздействие только одного фактора и к тому же предполагает, что это единственное влияние. Коэффициент эластичности от цен демонстрирует реакцию спроса на их изменение и полностью абстрагируется от влияния всех остальных факторов, в том числе и от дохода. В свою очередь коэффициент эластичности от дохода игнорирует роль цены в реакции спроса. Это противоречие усиливается в период инфляции, когда спад спроса, вызванный ростом цен, в какой-то мере компенсируется увеличением дохода. Выйти из положения можно с помощью расчетного показателя покупательной способности дохода, представляющего собой отношение цены к доходу на душу населения (показатель можно дифференцировать по социальным группам). Он интерпретируется как количество данного товара, которое можно купить на душевой доход при определенном уровне цены. Его формула имеет следующий вид:
где Кп.с.д. - показатель покупательной способности дохода; Дна душу - доход на душу населения; Рi - цена i-го товара.
Тогда коэффициент эластичности спроса от дохода и цены можно рассчитать как отношение двух темпов прироста - продажи и покупательной способности дохода:
Например, покупательная способность дохода при покупке масла животного с 1995 по 1997 г. выросла в 1,5 раза; темп прироста составляет 0,5. Продажа масла животного сократилась на 7%. Темп прироста составляет - 0,07. Коэффициент эластичности инфраэластичен: Э = 0,14. Такой же результат мы получим, если используем классическую формулу 5.36а:
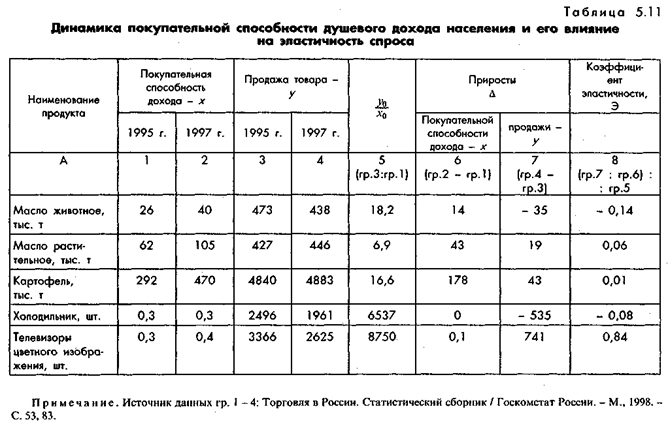
В качестве иллюстрации приведем данные за 1995-1997 гг. (табл. 5.11). Представлены только те товары, по которым обеспечена ассортиментная сопоставимость.
Расчет показывает, что в изучаемом периоде (в некоторой степени стабильном) рост дохода нейтрализует действие роста цен, поэтому все коэффициенты эластичности отражают значительную инфраэластичность спроса. Мы уже упоминали, что существует явление эластичности структуры спроса, которое проявляется в форме вытеснения одного товара другим под воздействием ценового фактора. Ученые давно заметили, что в определенных условиях изменение цены перестает влиять на спрос данного товара, но зато (часто, чтобы компенсировать рост затрат) изменяется спрос на какой-то другой товар. Это явление названо именем английского исследователя 30-х годов XX в. Дж. Хикса. Влияние изменения цены одного товара на спрос другого (или других) получило название перекрестной эластичности. Существуют различные методы ее анализа. Одним из наиболее распространенных является эмпирический коэффициент перекрестной эластичности, который исчисляется по следующей формуле:
где ЭA,B - коэффициент перекрестной эластичности спроса; DqA - прирост спроса на товар А; DpB - прирост цены на товар В; qB - спрос на товар В; рB - цена товара В.
Пример (цифры условные). В базисном периоде было продано 800 штук товара А и 400 штук товара В; в текущем - соответственно 500 и 400 штук. Прирост продажи товара А составил 300 штук. Цены товара В выросли с 40 до 60 руб./шт., т.е. прирост составил 20 руб./кг.
Это означает, что рост цены товара В на 1% привел к сокращению спроса на товар А на 1,5%. Эмпирический коэффициент эластичности широко используется в маркетинговом анализе, так как он весьма информативен и в то же время прост и доступен любому аналитику, однако у него имеется существенный недостаток, который мы уже отмечали. Расчет коэффициента эластичности по относительному показателю которым является покупательная способность дохода по существу паллиативное решение. Аналитику необходима информация, в какой мере каждый фактор в отдельности влияет на спрос при устранении воздействия всех остальных. Английские ученые Р. Аллен и А. Боули в 50-х годах преобразовали формулу Маршалла, «привязав» ее к уравнению регрессии Новый показатель получил название теоретического коэффициента эластичности, или формулы Аллена - Боули. В основе преобразования лежит исследование связей массовых явлении, при дифференцировании формула принимает вид
поскольку преобразование
где у' - первая производная соответствующей функции (табл. 5.4); x – факторный признак; ух – выровненное значение результативного фактора, т.е. выражение корреляционной зависимости: у = f (x). (см. формулу 5.14)
Ясно что для расчета теоретического коэффициента эластичности необходимо предварительно построить парное: ил.(много факторное уравнение регрессии, характеризующее связь между факторными признаками (ценой, доходом и т.д.) и результативным признаком (спросом). Эта проблема рассматривалась в гл.4. Формула теоретического коэффициента эластичности (см. формулу 5.33) позволяет определить реакцию спроса для каждой точки регрессионной кривой. Ее экономическая интерпретация, в частности, заключается в характеристике эластичности спроса отдельных контингентов (групп) потребителей. Если же брать совокупность в целом, то в формуле значения результативного и факторного признаков следует заменить на средние характеристики, т.е. будет определена средняя эластичность. При этом на практике обычно заменяют среднюю величину выровненного результативного признака (y̅x) средней величиной эмпирического значения результативного признака (у̅), поскольку суммы значений уx и у практически должны совпадать (незначительное расхождение может быть вызвано только округлением величин): Sух = Sу. Тогда формула коэффициента эластичности примет следующий вид:
где х̅i - среднее значение признака i-го фактора.
Данной формулой можно пользоваться при парных и множественной связях. В последнем случае строится многофакторная модель спроса (табл. 5.5). Тогда теоретический коэффициент эластичности определяется по каждому г'-му факторному признаку и считается чистым, т.е. освобожденным от влияния других факторов. Первая производная в практике маркетинговых исследований, как правило, не рассчитывается, а заимствуется из математических справочников. В табл. 5.12 приводятся производные наиболее употребительных функций.
Таблица 5.12
|


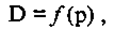 (5.22)
(5.22)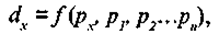 (5.23)
(5.23)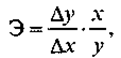 (5.24)
(5.24) . (5.24a)
. (5.24a)
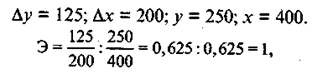
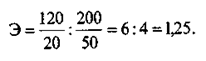
 (5.24б)
(5.24б) (5.24в)
(5.24в)
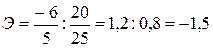 ,
,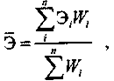 (5.26)
(5.26)
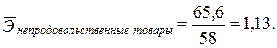




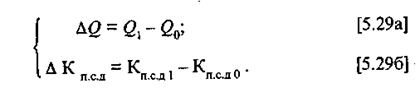

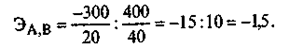
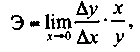 (5.31)
(5.31) есть
есть 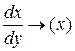 , т.е. первая производная у по х (ее обозначают через у'), то теоретический коэффициент эластичности приобретает следующий вид:
, т.е. первая производная у по х (ее обозначают через у'), то теоретический коэффициент эластичности приобретает следующий вид: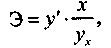 (5.32)
(5.32) (5.33)
(5.33)


